Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: June 14, 2025
In this article, we’re going to explore a few ways that we can store a tree structure in a relational database. For example, a family tree or a nested comment hierarchy would fit into such a model.
Relational databases are fantastic at storing tabular data, where some data relates to other data. We can very easily store data in two different tables which relate to each other. For example:

This is possible when the relationship points back to the same table, but it gets more complicated. Both in terms of reading the data back out again correctly, but also in terms of writing it and maintaining integrity. And this gets even more complicated if we want to have a deeply nested structure instead of just a single level of relationship.
If we want to read a single level of a nested tree structure, this is the same as any normal query. If we want to read an entire structure, though, we need to be able to traverse many levels of the tree. And worse, it might be an arbitrary number of levels, so we can’t just plan this into our query.
Conversely, if we want to write a new node at the bottom of a tree structure, then this is a simple write. If we want to write to the middle of the tree structure, though, or if we want to make updates across the entire structure, this gets very complicated very quickly and can risk breaking the integrity of the records.
The easiest way to achieve this is to forgo the relational database and store the structure in a JSON blob. This lets us ignore the complexity of reading and writing across many records and just store everything as a single record. We would then do any parsing and updating in our application code instead of our database.
The database engine will do many things for us automatically that we can’t benefit from here. However, doing this often loses more than it gains. For example, we lose the entire concept of referential integrity, both between nodes in the tree and between other tables. Because the whole tree is stored in a single record, it’s impossible to have database-controlled foreign keys that either point to individual nodes or point from individual nodes to other tables.
This also doesn’t scale very well. If we store the entire tree as a single record, there are limits on how big that record can get before it becomes too unwieldy to read and write.
Once we decide that we want to store every node individually, instead of storing the entire tree in one go, we need to decide the best way to achieve this.
One way to achieve this is to store on every node the ID of its immediate parent. Nodes that don’t have a parent would then store NULL, and nodes with a parent can store a reference to that parent. We could, for example, create our table as:
CREATE TABLE tree (
node_id INT PRIMARY KEY,
parent_id INT NULL REFERENCES tree (node_id),
.... other columns ....
);This would then allow us to store the following tree:
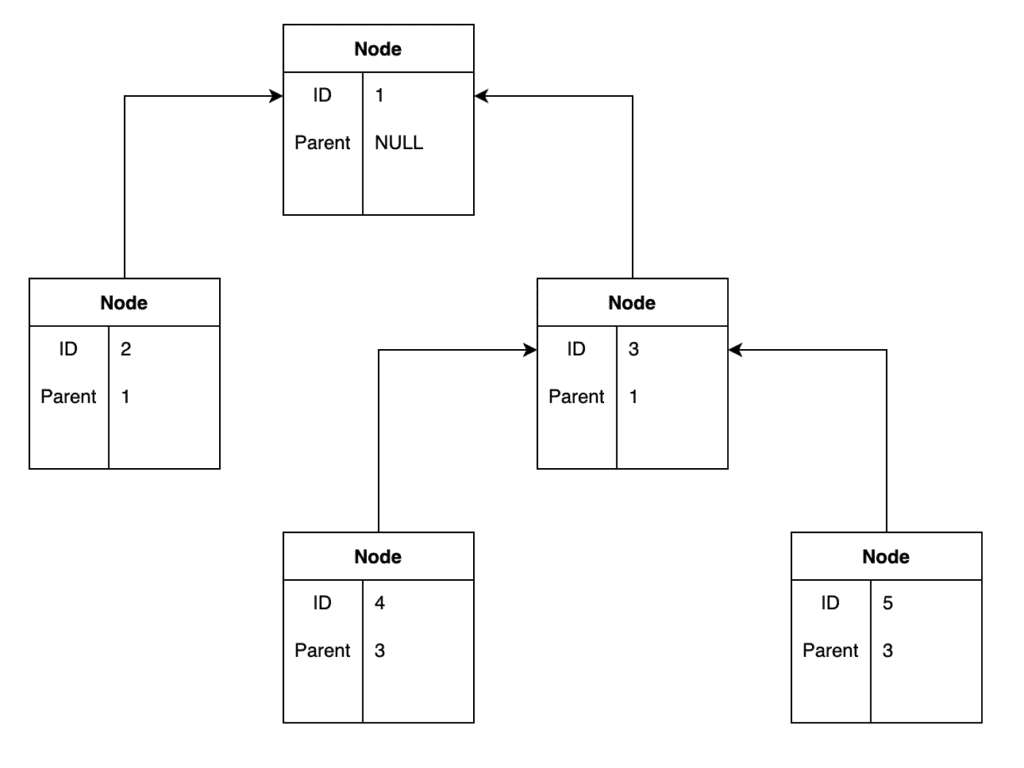
as follows:
| node_id | parent_id | Other Columns |
|---|---|---|
| 1 | NULL | … |
| 2 | 1 | … |
| 3 | 1 | … |
| 4 | 3 | … |
| 5 | 3 | … |
This gives us referential integrity within the database because we can ensure that values in the parent_id column are also present in the node_id column.
We can also very easily insert records into the tree in the correct place using a single statement:
INSERT INTO tree (node_id, parent_id) VALUES (6, 5);As well as moving a part of the tree to a different parent using a single statement:
UPDATE tree SET parent_id = 1 WHERE node_id = 4;However, reading the entire tree is more complicated here. Without extra database support – such as Recursive Common Table Expressions – we’d have to select each level of the tree individually and put it together in our application. Equally, reading the entire list of ancestors of a given node would also need to be done one at a time.
Obviously, this will be hugely inefficient, so how can we improve this?
If our database engine supports Recursive Common Table Expressions, it’s possible to use the WITH RECURSIVE clause to query a structure such as this in one go.
Doing this involves writing a query that essentially joins the table back onto itself and informs the database engine that it should recursively do this until it runs out of rows.
For example, to query the above table, we could do:
WITH RECURSIVE rectree AS (
SELECT *
FROM tree
WHERE node_id = 1
UNION ALL
SELECT t.*
FROM tree t
JOIN rectree
ON t.parent_id = rectree.node_id
) SELECT * FROM rectree;
This will start with selecting the node with node_id = 1, recurse down the tree finding rows where t.parent_id = rectree.node_id, until no more rows are returned. Similar queries can be written to traverse in the opposite direction if we need to list all ancestors instead of all child nodes.
This is the most efficient way to work with this kind of tree structure since we can cheaply insert records into the database and query the entire tree structure comparatively cheaply. However, not all database engines support this form of query, so it might not be an option for us. For example, MySQL supports this in 8.0 but not in earlier versions.
An alternative method to allow us to retrieve the entire tree is to have an extra column that identifies the tree to which each node belongs. This could be the ID of the root node, or some other identifier for the entire tree.
This means that our table gains an extra column, so we’re storing more data. It also means that inserting records into the table is slightly more complicated – because we need to provide both the immediate parent and the root of the tree. However, it means that we can now select every node within the same tree with a single query instead of needing many:
SELECT * FROM tree WHERE tree_id = 1;We can then put together the tree structure in memory due to this query.
Unfortunately, we can’t use this to select subtrees. We also can’t efficiently list all of the ancestors of a given node. The best we could do was to list the entire tree and work out the ancestors ourselves from the returned data.
However, this might not be an issue depending on our exact requirements.
We can use one other mechanism to store the graph separately from the nodes in what’s known as a Closure Table. This parallel table will store every ancestor for every node, including the distance between the node and its ancestor.
For example, the closure table for the above tree would be:
| node_id | parent_id | depth |
|---|---|---|
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 3 | 1 |
| 4 | 1 | 2 |
| 5 | 3 | 1 |
| 5 | 1 | 2 |
This lets us very easily search for entire subtrees and retrieve the whole set of ancestors for any given node.
However, inserting and updating nodes into the tree is more complicated. Depending on the depth of the node, we would have to create or update many records in our closure table. Moving nodes around is also very expensive because we would need to recalculate the closure table for every node in the subtree that is being moved.
Another alternative is to store the entire path in the tree rather than just the immediate parent. In this case, our above tree would be stored as:
| node_id | path | Other Columns |
|---|---|---|
| 1 | NULL | … |
| 2 | 1. | … |
| 3 | 1. | … |
| 4 | 1.3. | … |
| 5 | 1.3. | … |
Here, our path column is a string consisting of the IDs of every ancestor in the tree, separated by period characters. Some database engines support native arrays or similar constructs that could be used instead.
Doing this gives many benefits to reading data from our table. Every row has its entire hierarchy of parents as part of it. We can also query subtrees easily using the LIKE operator:
SELECT * FROM tree WHERE path LIKE '1.3.%';Note that we include a period right at the end, so that we can do matching without worrying about matching part of a node. For example, without a final period the following query query:
SELECT * FROM tree WHERE path LIKE '1.3%';would also incorrectly match anything that happens to contain values such as “1.30”.
Inserting new records into the tree is also relatively simple. We need to know the correct path for the node, which can be derived from the parent node. However, moving nodes around is more complicated. If we’re moving only a leaf node, this is the only path needing updating. But if we’re moving a node that has children, then the entire subtree needs updating, and every node will need to be updated in its way.
However, we lose referential integrity within the tree this way. We can’t have the database ensure that the parent nodes all exist correctly because they are just part of a structured string instead.
We would also need to see how efficient this is for our needs. LIKE matches on strings are less efficient than equality matches on integer keys, so if we don’t need subtree lookups, this might be less efficient for tangible benefit.
Here we have seen several techniques that can be used to represent hierarchical data in a relational database, along with the benefits and costs of each one. Next time you need to store such data and using a dedicated graph database isn’t an option, why not give one of these options a try.