The Stable Marriage Problem | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll study the stable marriage problem.

2. Problem

The stable marriage problem is finding a stable match between the sets of $n$ men and $n$ women. Each man has a preference order for the women; likewise, each woman has a preference order for the man.

Furthermore, there are no ties in the orderings. So, for each man $m$ and any two different women $w_i$ and $w_j$ , it holds that either $m$ prefers $w_i$ over $w_j$ or $w_j$ over $w_i$ . The same goes for every woman $w$ and two different men $m_i$ and $m_j$ .

We call matching between men and women unstable if it satisfies these two conditions:

There is a man $m$ that gets matched to a woman $w_{selected}$ but prefers another woman $w_{prefer}$
The woman $w_{prefer}$ is matched to another man $m_{selected} \neq m$ , but she prefers $m$

In other words, a matching is stable if and only if there doesn’t exist any pair $\boldsymbol{(m_{i}, w_{j})}$ such that both partners prefer other people, and those other people prefer them over their matches.

3. Example

Let’s check out an example.

Let $Y=\{John, Smith, Tony\}$ be men and $X=\{Anna, Bethany, Rose\}$ women. Let the men have the following preferences:

Here are the women’s preferences:

3.1. Marriage Matching

Let’s now define a marriage matching set $M$ . It has $n$ pairs. Each pair $\boldsymbol{(i, j)}$ contains members from $\boldsymbol{Y}$ and $\boldsymbol{X}$ such that each man $\boldsymbol{i}$ from $\boldsymbol{Y}$ is paired with exactly one woman $\boldsymbol{j}$ from $\boldsymbol{X}$ and vice versa.

Further, we call a pair $(i, j)$ , where $i \in Y$ and $j \in X$ , a blocking pair for a marriage matching $M$ if man $i$ and woman $j$ aren’t matched in $M$ despite preferring each other to their chosen mates in $M$ .

For example, $(John, Bethany)$ is a blocking pair for the marriage matching $M = \{(John, Anna), (Smith, Bethany), (Tony, Rose)\}$ . This is so because $John$ wants $Bethany$ more than $Anna$ , while $Bethany$ prefers $John$ over $Smith$ .

3.2. Matching Stability

We conclude this section by describing the stability of a matching.

We call a marriage matching $\boldsymbol{M}$ stable if and only if there is no blocking pair for it. Otherwise, we say $M$ is unstable. Hence, we find the matching $M =\{(John, Anna), (Smith, Bethany), (Tony, Rose)\}$ unstable because $John$ and $Bethany$ prefer each other over their matches.

4. Algorithm

All the men and women are initially free, so the matching $M$ is empty. After that, we perform the following steps iteratively:

First, we randomly select a man $m \in Y$ and let him propose to the first woman $w$ on his preference list that hasn’t rejected him so far
Then, if $w$ is free, she accepts his proposal, and they become a pair $(m, w)$ in $M$ . If $w$ is not free, she compares $m$ with her current match $m_{current}$ . If she prefers $m$ to $m_{current}$ , she accepts the $m$ proposal and replaces $m_{current}$ with $m$ . This way, we get a new pair $(m, w)$ . Otherwise, $w$ rejects the proposal of $m$ , and $m$ remains unmatched

We iterate these two steps until no man $m \in Y$ remains unmatched. Since no two men get matched with the same woman, all the women have their matches when the algorithm terminates.

4.1. Pseudocode

Now, we look at the pseudocode for this algorithm:

5. Working Example

Let’s run this algorithm on the example from above.

5.1. Initiation

Initially, all three men in $Y=\{John, Smith, Tony\}$ are free and so are all three women in $X=\{Anna, Bethany, Rose\}$ :

5.2. Iterations

Let’s say we randomly chose $John$ to start with. $John$ proposes to $Bethany$ since he prefers her over the rest, and she accepts since she is currently free. So, we have $M=\{(John, Bethany)\}$ after the first iteration:

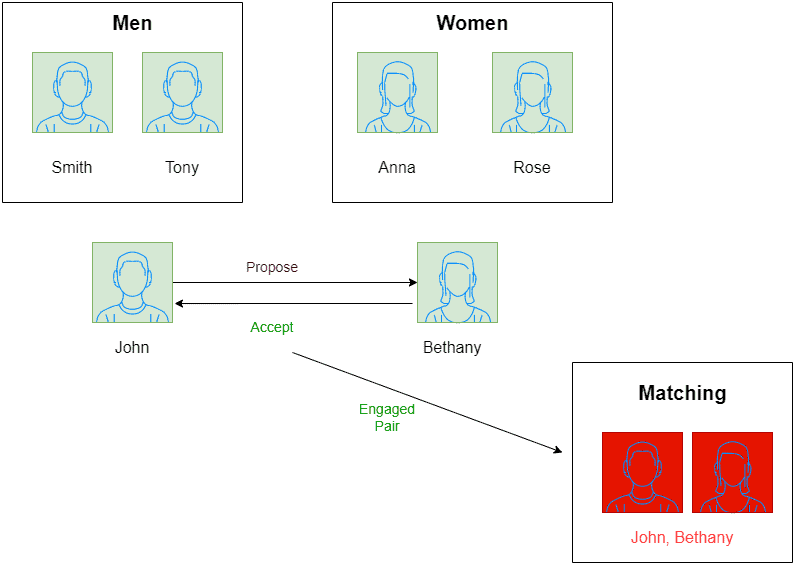
Let $Smith$ be the next free man to match. $Smith$ proposes to $Bethany$ but since $Bethany$ prefers $John$ over $Smith$ , she rejects him:

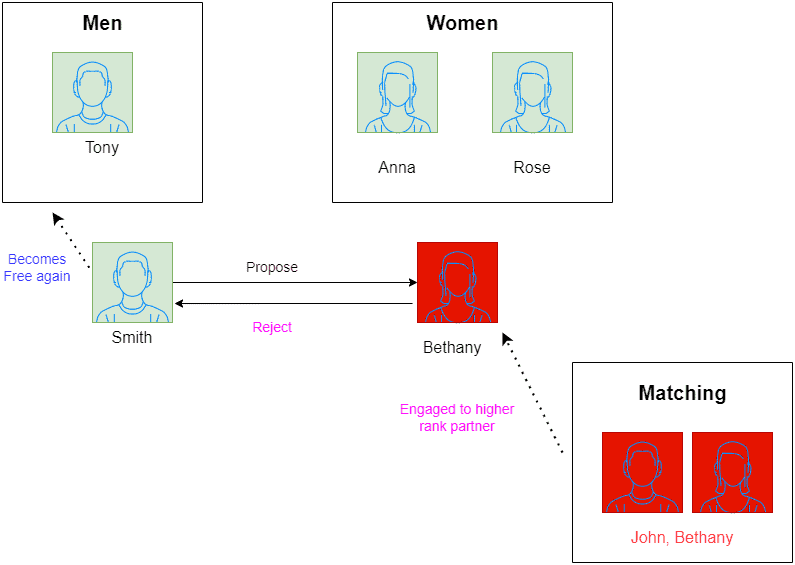
Let’s say we randomly chose $Smith$ again in the next iteration. Now, he proposes to $Rose$ , who is next on his priority list. $Rose$ is free, so she accepts, and we get a new pair $(Smith, Rose)$ , which we add to $M$ to get $M=\{(John, Bethany), (Smith, Rose)\}$ :

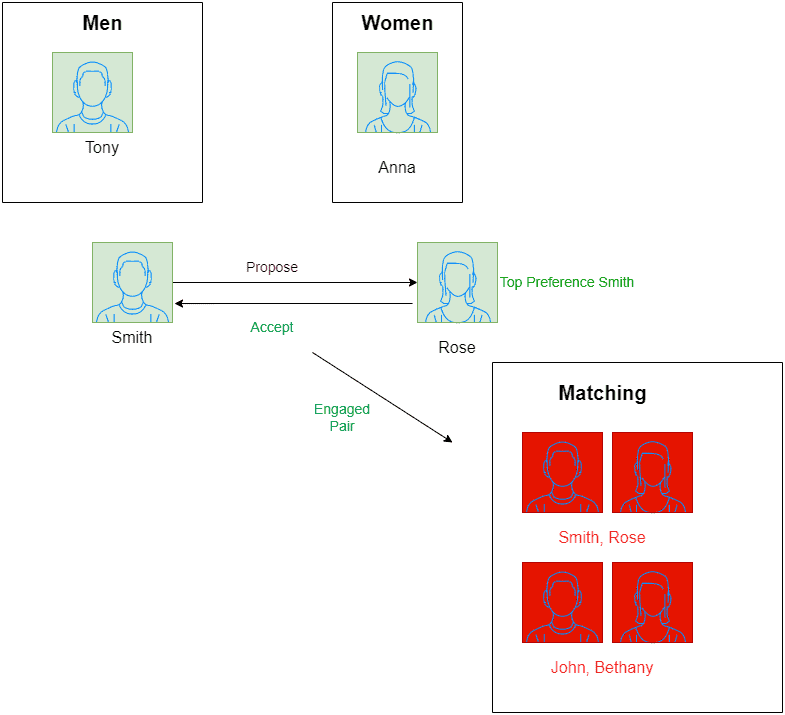
Next, our only choice is $Tony$ since he’s our last free man. He proposes to $Rose$ but since $Rose$ prefers $Smith$ over $Tony$ , she refuses $Tony$ and stays with $Smith$ :

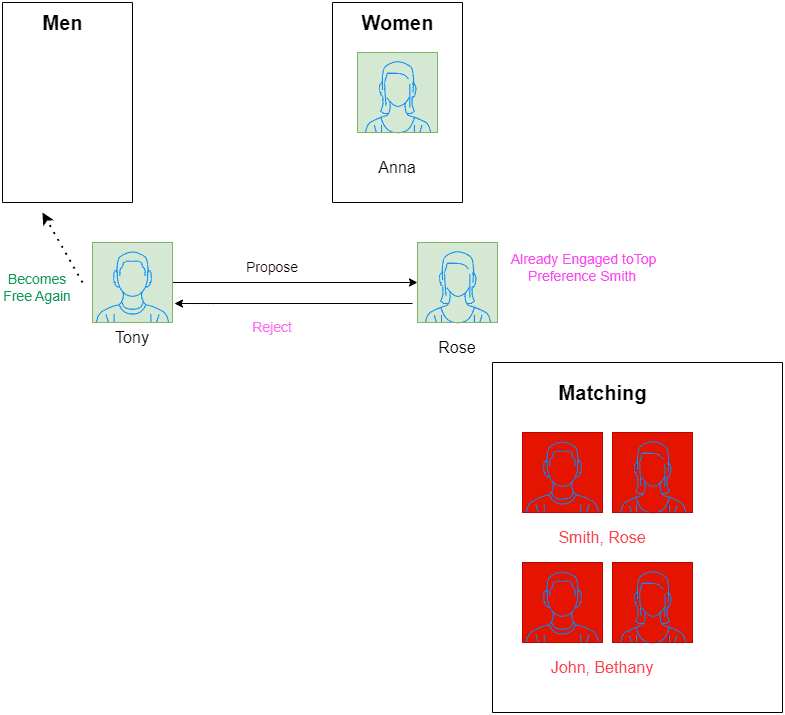
Then, Tony proposes to $Bethany$ . Since $Bethany$ prefers $Tony$ the most, she ditches $John$ and accepts $Tony$ . So, our matching changes to $M= \{(Smith, Rose), (Tony, Bethany)\}$ :

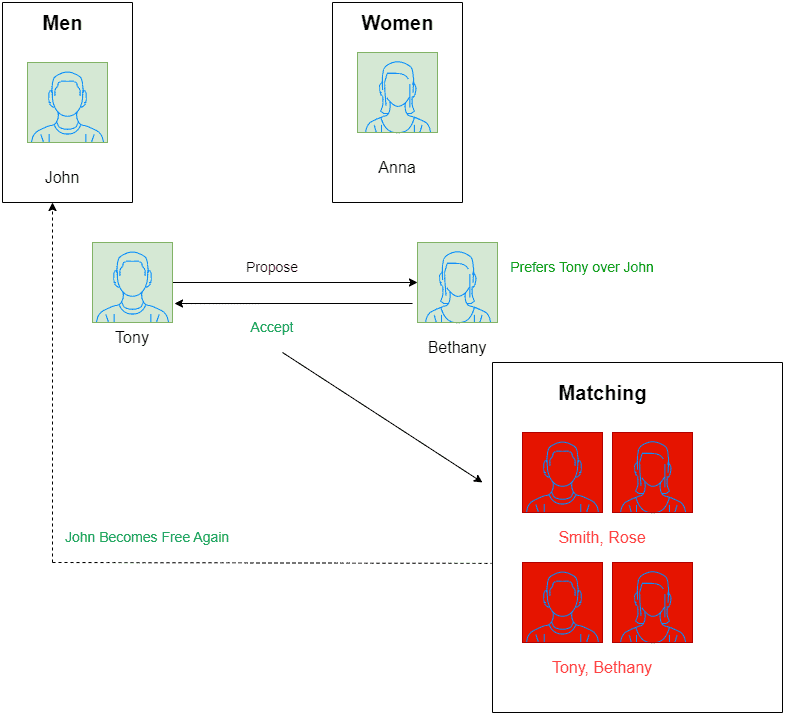
Now, we pick $John$ as the next free man. Since $Bethany$ already rejected $John$ , $John$ proposes $Anna$ , the next girl on his ranking list. $Anna$ is free, so she accepts the proposal. As a result, we get the matching $M=\{(Smith, Rose), (Tony, Bethany), (John, Anna)\}$ :

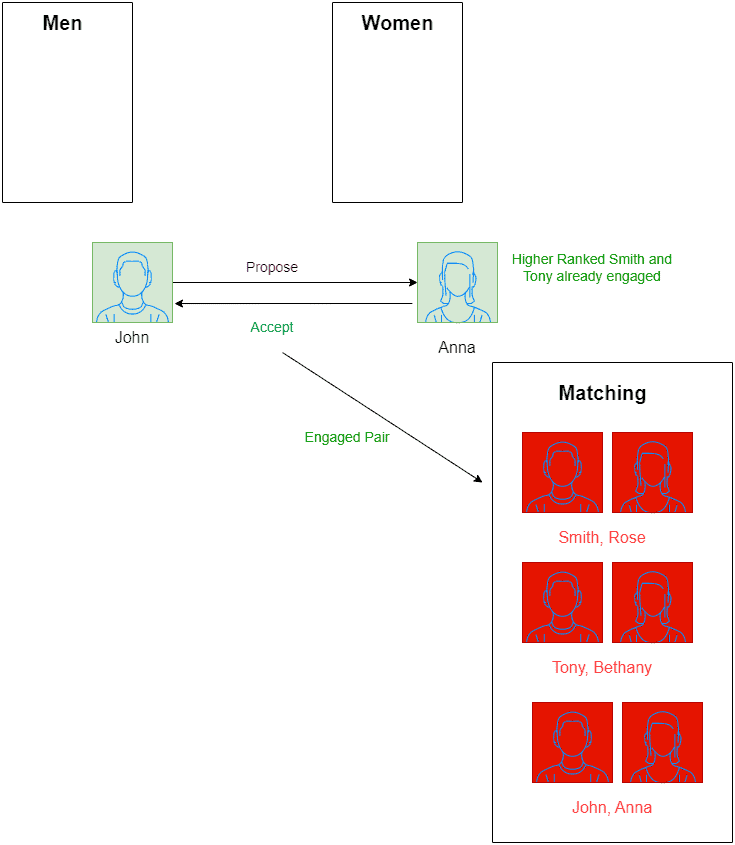
We stop here since no man is free anymore.

6. Theory

In this section, we talk about the correctness of this algorithm and prove that it always terminates.

6.1. The Algorithm Always Terminates

This algorithm terminates after $\boldsymbol{n^{2}}$ iterations at most.

Why? Because we start with $n$ free men, each of which has a preference list of $n$ women. Thus, we have the total of $n^{2}$ women in the matrix of the men’s preferences. In each iteration, we take one man, and that man proposes to one woman in the order of preference. Irrespective of the woman accepting or refusing, we reduce the total number of women in his preference list by 1. This is so because we rule out any man proposing to the same woman more than once by removing any woman he proposed to from his preference list.

Hence, our algorithm must terminate after at most $n^{2}$ iterations. In the end, each man gets matched to a unique woman.

6.2. Correctness

Now, we show that our final matching $M$ is a stable marriage matching. The termination property shows that each man in $Y$ is matched to a unique woman in $X$ . So, we need to show the stability of this assignment.

We prove this by contradiction. Let’s say that $M$ is unstable. So, this implies that a blocking pair $(m, w)$ exists such that both partners prefer each other but aren’t matched in $M$ . So, in $M$ , we have man $m$ matched to another woman $w_{other}$ and woman $n$ matched to another man $m_{other}$ .

Further, $m$ proposes to every woman on his ranking list (sorted from the highest to the lowest preference order), and $(m, w_{other})$ got included in $M$ before $(m, w)$ . So, we know that $m$ must have proposed to $w_{other}$ before proposing to $w$ . That’s only possible if he prefers $w_{other}$ to $w$ . However, that’s a contradiction since we assumed there’s a blocking pair in which he prefers $w$ to $w_{other}$ . As a result, we conclude no blocking pair can exist, which proves the matching $M$ this algorithm returns is stable.

7. Space and Time Complexity

This algorithm has time complexity of $\boldsymbol{O(n^{2})}$ . In the worst case, each man finds his match after proposing to all the other women. So, we make $n$ iterations for each man and $n$ to change their respective partners. Hence, the time complexity is $O(n^{2})$ . However, a necessary assumption is that women can compare two men in constant time.

The space complexity of this algorithm is ${O(n^{2})}$ since the male and female preference lists require ${O(n^2)}$ space.

8. Real World Application

This problem can have multiple real-world applications.

First, this algorithm can match first-time resident doctors to hospitals. Each participating hospital and resident doctor prepares their preference list. Then, the algorithm for stable marriages matches the residents-to-be with hospitals to get a stable matching.

Second, we can use this to help the central admission system to match students with universities as per the students’ and universities’ preference lists. Since this algorithm is stable and always terminates, we guarantee that a student gets a school from his preference list. Further, the student can’t secure admission to a more preferred school (than what he got from the system) by manipulating their preferences. This is how the admissions system works in India for most engineering schools.

9. Conclusion

In this tutorial, we studied the stable matching problem. The goal is to find a stable matching for elements of two sets (each having $n$ elements) based on each element’s given matching preferences. We can solve it in $\boldsymbol{O(n^{2})}$ time and $\boldsymbol{O(n^{2})}$ space.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex