1. Overview
In this tutorial, we’ll talk about the problem of finding the shortest cycle in an undirected graph.
First, we’ll define the problem and provide an example to explain it. Then, we’ll present a solution for this problem and work through its implementation and time complexity.
2. Defining the Problem
Suppose we have a connected undirected graph 
that contains 
vertices and 
edges. We were asked to get the shortest cycle length in the given graph . (Recall the cycle is a path that starts from a given vertex and ends at the same vertex).
Let’s take a look at the an undirected graph for a better understanding:
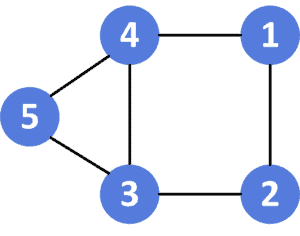
As we can see, there are several cycles in the previous graph:
, with length 
.
, with length 
.
, with length 
.
Therefore, the answer for the given graph would be equal to .
3. Solution
3.1. Main Idea
The main idea of this approach is to use DFS traversal on the given graph. For each visited node, we’ll have a cycle of length equal to the current node’s depth minus the previous node’s depth.
First, we’ll run a normal DFS traversal on the given graph . Second, for each node we visit, we’ll mark it visited and store the depth of it. Then, if we reach a node that has been visited before. This case will create a cycle with a length equal to the current depth of DFS traversal minus the node’s depth that we’ve stored before.
Finally, the shortest cycle length in the graph will be the minimum value among all the DFS calls.
3.2. Algorithm
Let’s take a look at the implementation of the algorithm:
Initially, we have the 
function that will return the shortest cycle length in the given graph . The function will have five parameters: the adjacency list of the graph , the current 
, the parent of the current node 
, the current depth 
in the DFS traversal, and the 
array, which will store the depth of each visited node. The initial value for all unvisited nodes is 
.
First, we check if the of the current node is not equal to , which means this node has been visited before, and we have a cycle. So, we return the length of this cycle, which is equal to the current depth minus the of the current .
Second, if the previous condition is not met, this is not visited yet. So, we update the of it to be equal to the current depth .
Third, we declare 
, which will store the length of the shortest cycle with an initial value equal to infinity. Then, for each neighbor 
of the current , we’ll call our function on it, increase the current depth by one, and try to minimize the value.
Note that we used all the neighbors of the current node, except for the parent. The parent is the node that we visited right before the current one. This is because, since it’s an undirected graph, each edge can be crossed in both directions.
This will cause our answer to always be equal 
from the option of going back and forth any edge. Thus, we don’t return directly to the parent node but move to visit other nodes.
Finally, the call 
will return the length of the shortest cycle in the given graph .
3.3. Complexity
The time complexity of this approach is 
, where is the number of vertices of the given graph , and is the number of edges. The reason behind this complexity is that we’re visiting each vertex at most twice, and each edge at most once.
The space complexity here is 
. since we’re storing the depth of each vertex.
4. Conclusion
In this article, we discussed the problem of finding the shortest cycle in an undirected graph. We defined the problem and provided an example to explain it.
Finally, we provided a DFS approach to solve it and walked through its implementation and time complexity.