How to Implement a Queue Using Two Stacks?

1. Overview

When thinking about data structures, a queue and a stack differ in their handling of elements. A queue operates in a First-In-First-Out (FIFO) manner, while a stack works as a Last-In-First-Out (LIFO).

In this tutorial, we’ll explore implementing a queue using two stacks.

2. Why Two Stacks?

A queue typically allows these key operations:

• push(): Add an element to the back of the queue
• pop(): Remove the front element from the queue
• peek(): Return the front element without removing it
• isEmpty(): Check if the queue is empty

A stack, by definition, can’t maintain the FIFO order. However, by using two stacks (s1 and s2), we can manage this constraint:

• s1 will hold the elements of the queue in the correct order
• s2 is an auxiliary stack to reverse the order

There are two approaches to implementing a queue using two stacks:

• Push – O(n) per operation, Pop – O(1) per operation
• Push – $O(1)$ per operation, Pop – Amortized $O(1)$ per operation

We’ll see each approach with an example.

3. Slower Push and Efficient Pop

Let’s go through each operation along with their time and space complexity.

3.1. push()

We first transfer all s1 elements to auxiliary stack s2. Then the newly arrived element is pushed on top of s2 and all other elements from s2 are popped and pushed to s1.

Let’s have a look at the implementation:

s1 <- new Stack
s2 <- new Stack

algorithm push(int x):

    // INPUT
    // x = element to be pushed in stack
    // OUTPUT
    // element pushed to stack

    if (s1 is empty):
        top <- x
    while s1 is not empty:
        s2.push(s1.pop())
    s2.push(x)
    while s2 is not empty:
        s1.push(s2.pop())

In the worst case, every element has to be moved twice (from s1 to s2 and back), so the time complexity will be O(n). The space complexity will also be O(n) since we use additional space for the second stack, proportional to the number of elements.

3.2. pop()

We can directly remove the top element from s1. Since s1 maintains the correct order i.e. front at the top, the pop operation is straightforward:

algorithm pop():
    // OUTPUT 
    // top element popped from stack

    result <- s1.pop()
    if (s1 is not empty):
        top <- s1.peek()
    return result

Popping an element from the stack is a constant-time operation, so the time complexity is O(1). The space complexity is also O(1), as no extra space is required other than for the result.

3.3. peek()

The front element is always available at the top of s1:

algorithm peek():
    // OUTPUT 
    // return top element from stack

    return top;

This allows us to return it in constant time, so the time complexity is O(1) and space complexity is O(1) since no extra space is used.

3.4. isEmpty()

At last, to check if the queue is empty, we can verify whether s1 is empty:

algorithm empty():
    check and return if s1 is empty

The time and space complexity to check if the queue is empty is O(1).

3.5. Example

Let’s walk through a dry run for each approach with the following sequence of operations:

push(1)
push(2)
push(3)
pop()
push(4)
pop()

Initial State: s1 = [], s2 = [].

push(1): Push 1 to s1. Since there are no elements in s1 initially, no elements are moved to s2. After that, no elements need to be moved back from s2 to s1, as both stacks are still empty apart from the newly pushed element.

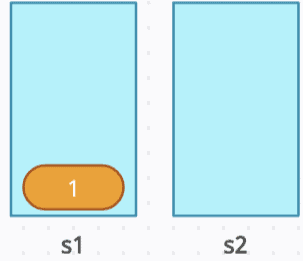
push(2): Move all elements from s1 to s2, resulting in s1 being empty and s2 containing [1]. Then, push 2 onto s2. Afterwards, move the elements back from s2 to s1, so s1 holds [2, 1] and s2 is empty again.

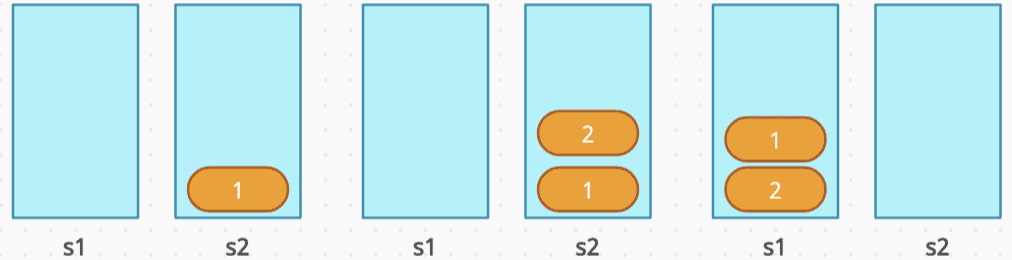
push(3): Move all elements from s1 to s2, leaving s1 empty and s2 containing [1, 2]. Next, push 3 onto s2. Finally, move the elements back from s2 to s1, resulting in s1 holding [3, 2, 1] and s2 being empty.

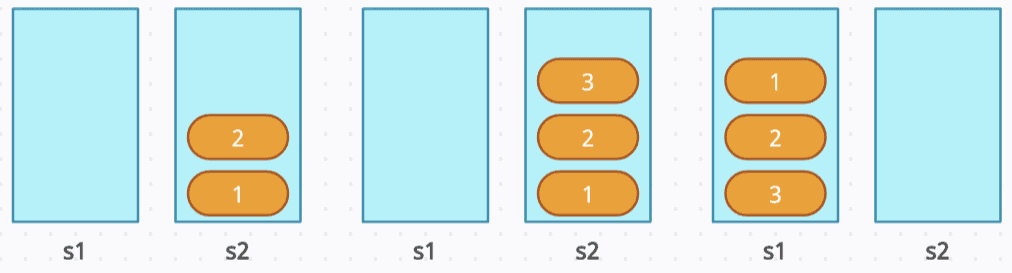
pop(): Pop from s1, resulting in s1 = [3, 2]. The front of the queue, which is 1, is removed.

push(4): Move all elements from s1 to s2, leaving s1 empty and s2 containing [2, 3]. Then, push 4 onto s2. Afterward, we move the elements back from s2 to s1, resulting in s1 holding [4, 3, 2] and s2 being empty.

pop(): Pop from s1, resulting in s1 = [4, 3]. The front of the queue, which is 2, is removed.

4. Efficient Push and Amortized Pop

In this second approach, we aim to make the push operation O(1) while maintaining an efficient pop operation with amortized O(1) time complexity. This method leverages two stacks (s1 and s2) to simulate a queue, similar to the first approach but with an important optimization: the elements are only moved between the two stacks when necessary.

Here’s how this method works:

4.1. push()

In this approach, pushing an element is a straightforward process. The new element is added to the top of s1. There is no need to shuffle elements between stacks during the push.

Here is the implementation:

s1 <- new Stack
s2 <- new Stack

algorithm push(int x):

    // INPUT
    // x = element to be pushed in stack 
    // OUTPUT
    // element pushed to stack
    if (s1 is empty):
        top <- x
    s1.push(x)

Since adding an element to the top of the stack is a constant-time operation, the time complexity is O(1). The stack grows linearly with the number of elements added to the queue, so the space complexity is O(n).

4.2. pop()

In this method, we pop elements from s2. If s2 is empty, we transfer all elements from s1 to s2 for reversing the order of elements. This way, the first element inserted into s1 ends up on top of s2, simulating the FIFO behavior of a queue.

This approach is slightly efficient because the transfer from s1 to s2 happens only when s2 is empty. Once the transfer is done, each element can be popped from s2 in constant time:

algorithm pop():

    // OUTPUT 
    // top element popped from stack
    if (s2 is empty):
        while si is not empty:
            s2.push(s1.pop())
    return s2.pop()

Transferring elements from s1 to s2 takes O(n); in the worst case, it only happens once per n pop operations, resulting in an amortized O(1) time complexity. Since both stacks are used together to store all the elements, the space complexity is proportional to the number of elements.

Now, what exactly does amortized time complexity mean?

The amortized time complexity gives a more realistic performance estimate when dealing with sequences of operations. In this case:

• The push operation is O(1).
• The pop operation is O(1) in most cases. We need to move elements from s1 only when s2 is empty, which costs O(n) but happens infrequently.

For example, if we perform n push operations followed by n pop operations:

• The push operations take O(n) in total.
• The pop operations take O(2n) (O(n) for transferring elements and O(n) for the pop operations), which averages out to O(1) per pop over time.

4.3. peek()

The peek operation can be handled similarly to pop. If s2 is’nt empty, the top of s2 holds the front of the queue. If s2 is empty, we first transfer elements from s1 to s2, then return the top of s2:

algorithm peek():

    // OUTPUT
    // return top element from stack
    if (s2 is not empty):
        return s2.peek()
    return top;

Once elements are in s2, peeking is a constant-time operation, so the time complexity is O(1). We did’nt use any extra space for the peek operation, so the space complexity is also O(1).

4.4. isEmpty()

To check if the queue is empty, we verify whether both s1 and s2 are empty:

algorithm empty():
    check and return if s1 and s2 are empty

This operation checks the sizes of two stacks, so the time complexity is O(1) and the space complexity is O(1), since no extra space is used.

4.5. Example

Let’s walk through a dry run for each approach with the same sequence of operations used in the previous section.

push(1)
push(2)
push(3)
pop()
push(4)
pop()

Initial State: s1 = [], s2 = [].

push(1), push(2), push(3): Push [1,2,3] to s1. Since there are no elements in s1 initially, no elements are moved to s2.

push(1), push(2), push(3): Push [1,2,3] to s1. Since there are no elements in s1 initially, no elements are moved to s2.

pop(): Since s2 is empty, move all elements from s1 to s2 until s1 is empty and s2 = [3, 2, 1]. Then, pop from s2, leaving s2 = [3, 2] and removing the front element, 1.

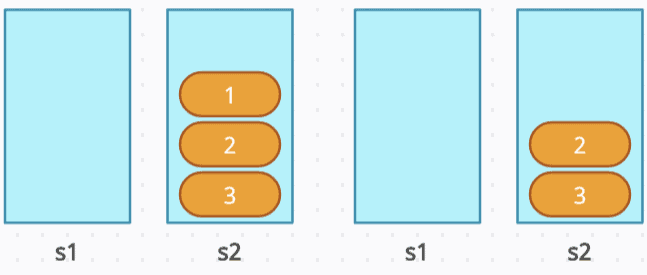
push(4): Push 4 to s1.

pop(): Since s2 is’nt empty, simply pop from s2, leaving s2 = [3]. The front of the queue, which is 2, is removed.

5. Conclusion

In this article, we saw that the two approaches to implementing a queue using two stacks both rely on the same idea of leveraging the properties of two LIFO (Last-In-First-Out) stacks to simulate FIFO (First-In-First-Out) queue behavior. However, they differ in terms of when and how they manage the transfer of elements between the stacks, which leads to different time complexities for push and pop operations.

The first approach is better suited for frequent pop operations. Since all elements are already in the correct order in s1, the pop operation is very efficient. However, the cost is shifted to the push operation, which requires O(n) time as the elements are rearranged each time a new one is pushed.

The second approach is better suited for frequent push operations. Each push is O(1), but the cost of rearranging elements is deferred to the pop operation. The amortized O(1) pop time makes it efficient over multiple operations, but a single pop might require an O(n) transfer of elements from s1 to s2.