Go-Back-N Protocol | Baeldung on Computer Science

1. Introduction

Go-Back-N and Selective Repeat protocols are fundamental sliding window protocols that help us better understand the key idea behind reliable data transfer in the transport layer of computer networks.

In this tutorial, we’ll describe how the Go-Back-N protocol works. Moreover, we’ll discuss the relationship between the window size $N$ and the sequence number space size $S$ as well as how the selection of $N$ affects the algorithm’s performance.

2. Go-Back-N

The sliding window (pipelined) protocols achieve utilization of network bandwidth by not requiring the sender to wait for an acknowledgment before sending another frame.

In Go-Back-N, the sender controls the flow of packets, meaning we’ve got a simple and dummy receiver. Therefore, we’ll start by discussing how the server handles data packets first.

2.1. The Sender

The sender has a sequence of frames to send. We assume a window size of $N$ . Furthermore, there exist two pointers to keep track of send base ( $send\_base$ ) and the next packet to send ( $nextseqnum$ ).

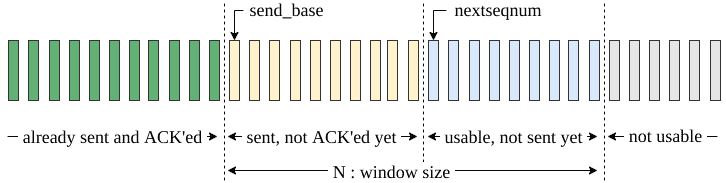
First of all, the sender starts by sending the first frame. Initially, $send\_base = 0$ and $nextseqnum = 0$ . While there are more packets to send and the $nextseqnum$ is smaller than the $send\_base + N$ ; the sender sends the packet pointed by the $nextseqnum$ pointer and then increments the $nextseqnum$ .

Meanwhile, the $send\_base$ is incremented after receiving acknowledgment packets from the receiver. The reception of duplicate ACK messages does not trigger any mechanism.

There is a single timer for the whole sending window, which measures the timeout for the packet at the $send\_base$ . Therefore, if a timeout occurs, the sender restarts the timer and re-transmits all the packets in the sending window starting from $send\_base$ .

To summarize, we can represent the sender’s algorithm with the following pseudocode:

algorithm Sender():
    // OUTPUT
    //    Manages sending of packets following the Go-Back-N protocol
    
    send_base <- 0
    nextseqnum <- 0
    
    while true:
        if nextseqnum < send_base + N:
            send packet nextseqnum
            nextseqnum <- nextseqnum + 1
        
        if receive ACK n:
            send_base <- n + 1
            if send_base = nextseqnum:
                stop timer
            else:
                start timer
        
        if timeout:
            start timer
            for i <- send_base to nextseqnum - 1:
                send packet i

2.2. The Receiver

The receiver implementation of the Go-Back-N is as simple as possible:

The receiver only keeps track of the expected sequence number to receive next: $nextseqnum$ .

There is no receiver buffer; out of order packets are simply discarded. Similarly, corrupted packets are also silently discarded.

It always sends the acknowledgment for the last in-order packet received upon reception of a new packet (successfully or unsuccessfully). As a result, it will generate duplicate acknowledgment messages if something goes wrong.

As a summary, the pseudocode for the receiver’s algorithm is:

algorithm Receiver():
    // OUTPUT
    //    Manages receiving of packets following the Go-Back-N protocol
    
    nextseqnum <- 0
    
    while true:
        if a packet is received:
            if the packet is not corrupted and sequence_number = nextseqnum:
                deliver data to upper layer
                send ACK nextseqnum
                nextseqnum <- nextseqnum + 1
            else:
                // The packet is corrupted or out of order, so we drop it
                send ACK nextseqnum - 1

On the whole, this concludes the explanation of the ACK-based, NAK-free Go-Back-N protocol, which covers the issues related to reliable data transfer by use of sequence numbers, cumulative acknowledgments, checksums, and timeouts/retransmissions.

3. Cumulative Acknowledgements and Sequence Numbers

The Go-Back-N protocol adopts the use of cumulative acknowledgments. That is, receiving acknowledgment for frame $\textbf{n}$ means the frames $\textbf{n-1}$ , $\textbf{n-2}$ , and so on are acknowledged as well. We denote such acknowledgments as ACK $n$ .

Let $S$ denote the maximum possible sequence number we use to mark the frames. Again assume we have a window size of $N$ .

Now, let’s imagine a simple scenario:

The sender sends the frames in the window, enumerating them from 0 to $S$
As a response it receives ACK $S$ , marking frames $S$ , $S-1$ , and so on acknowledged
Then the sender sends the second set of frames, again enumerating them from 0 to $S$
After that, the sender receives another ACK $S$

In the sender’s perspective, what does the acknowledgment in the last step stand for? Did all the packets in the second batch got lost or sent successfully? If $S = N$ , there is no way that the sender knows the real outcome. That’s why we must have strict inequality $\textbf{N}$ < $\textbf{S}$ .

4. Utilization and Window Size

As we stated before, pipelined protocols are an improvement over the stop-and-wait protocol. To achieve better network utilization, we have multiple frames “in-flight” between the sender and the receiver at a given time.

$N$ denotes the window size in Go-Back-N, which the sender is allowed to send before receiving an acknowledgment. Basically if $N = 1$ , we have a stop-and-wait implementation.

The maximum possible link utilization formula, disregarding any overheads is:

$Utilization \leq \frac{N}{1 + 2 \times BD}$

In the formula, $BD$ is the bandwidth-delay product, representing how much data can be carried over the link at a given time. It’s calculated as the data link’s capacity multiplied by round-trip delay time.

Theoretically, we find the maximum possible $\textbf{N}$ by solving the equation above for $\textbf{Utilization = 1}$ . However, in practice, we need to use an even smaller $\textbf{N}$ value.

There are two main reasons for this.

First of all, we need to consider at which rate the receiver can process the packets arrived as well as having high network utilization.

If the receiver cannot cope up with processing the packets, it will drop them. In this case, the sender will be retransmitting the same packets over and over again, the successfully transmitted package rate will be inadequately low. Hence, achieving high utilization is meaningless.

The concept of preventing a fast sender from drowning a slow receiver in data is called flow control. Flow control enforces a smaller window size $N$ , concerning the receiver’s processing speed.

Second, though equally important is to limit the window size $\textbf{N}$ is congestion control. Too many packets being present in (a part of) the network cause packet delays and packet loss, which degrades performance. Indeed, a sender should respect each element in the network so that the overall network performance is utilized.

5. Conclusion

To sum up, the Go-Back-N protocol works for both the sender and the receiver side to ensure reliable data transfer.

We also discussed how the cumulative acknowledgments are enforcing us to use an $S$ value greater than $N$ and how to select a reasonable window size $N$ to achieve better utilization.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex