Using GANs for Data Augmentation

1. Overview

In this tutorial, we’ll talk about using Generative Adversarial Networks (GANs) for Data Augmentation. First, we’ll introduce data augmentation and GANs, and then we’ll present a GAN architecture that manages to generate very realistic samples.

2. Data Augmentation

Deep learning revolutionized numerous fields and has become the state-of-the-art approach to many complex tasks like text translation, image segmentation, and automatic speech recognition. Large annotated datasets play a critical role in this success since deep learning models need a lot of data to be trained on. However, it is sometimes difficult and expensive to annotate a large amount of training data. Therefore, proper data augmentation is useful to increase the model performance.

To better explain the concept with examples, we’ll focus on data augmentation for images, but the methods are the same regardless of the domain. Generally, the goal of data augmentation is to increase the size of the dataset by changing a property of already existing data or generating completely new synthetic data.

Usually, the former approach is followed where we flip, rotate, or randomly change the hue, saturation, brightness, and contrast of an image. The procedure is simple and can be done online while training the model. The disadvantage of using these techniques is that we don’t introduce new synthetic data to the model, but we just include the same samples in a different state. Hence, the model has already seen these samples, and the impact on generalizability is limited:

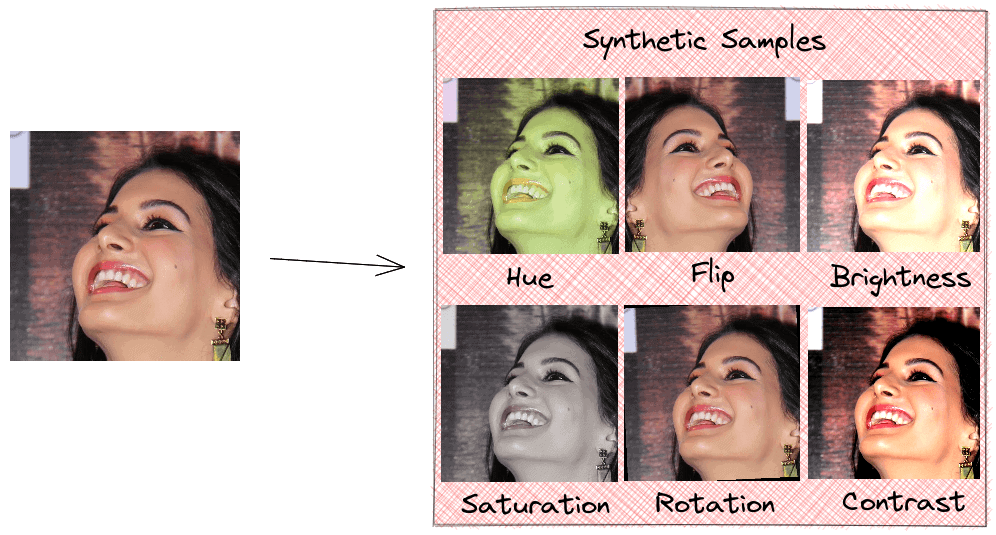
Generating new realistic synthetic data is a difficult task that includes learning to mimic the original distribution of our dataset. As we’ll see, GANs can generate realistic samples and improve the model performance.

3. GANs

Let’s first make a brief introduction to their structure that consists of two parts.

A generator that learns to generate plausible data. It takes as input a fixed-length random vector and learns to produce samples that mimic the distribution of the original dataset. The generated samples then become negative examples for the discriminator.

A discriminator that learns to distinguish the generator’s synthetic data from real data. It takes as input a sample and classifies it as “real” (comes from the original dataset) or “fake” (comes from the generator). The discriminator penalizes the generator for producing implausible samples:

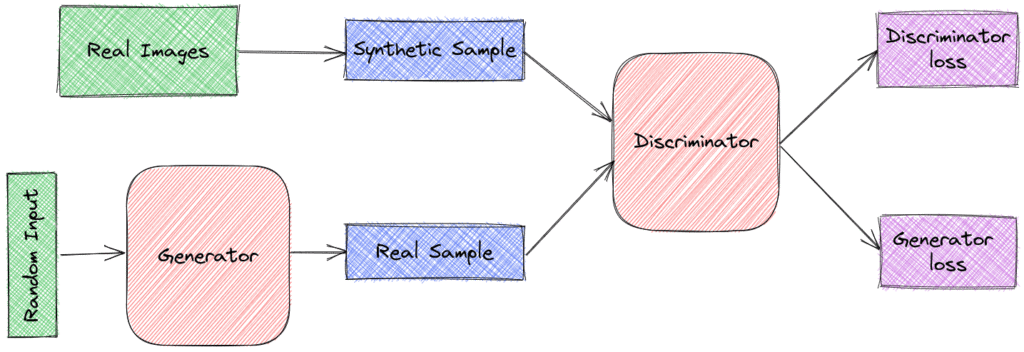
In the case of images, both the generator and the discriminator are CNNs, and the goal of the generator is to generate images that are so realistic that the discriminator thinks they are real. Then, using backpropagation to update the weights and biases of these models over time, the generator will slowly learn to create samples that mimic the physical and mathematical distribution of the original dataset.

The models play a two-player minimax game, such that optimizing the objective function of the discriminator negatively impacts the objective function of the generator and vice versa. Specifically:

• The generator wants to minimize where is the random input to the generator. By minimizing this term, the generator fools the discriminator in classifying the fake samples as real ones.
• The discriminator wants to maximize where are the samples from the original dataset. This term corresponds to the probability of assigning the correct label to both the real samples and the samples from the generator.

4. Conditional GANs

In few-shot learning settings, we want to train a model for predictions based on a limited number of samples. For example, let’s suppose we want to create a model that takes as input an image with a dog and predicts its breed. We have huge datasets with animals available, but the amount of data annotated with dog breeds is very limited. Here, the solution is to augment our dataset using GANs.

Although regular GANs can generate very realistic samples when they are trained on a vast amount of data, they are not able to generate samples with a specific label. Conditional GANs deal with this problem by modifying the original generator network to control its output. Specifically, there are two major changes in the network.

We add a label to the input of the generator and try to generate the corresponding data point.

The discriminator takes as input both the sample and the corresponding label :

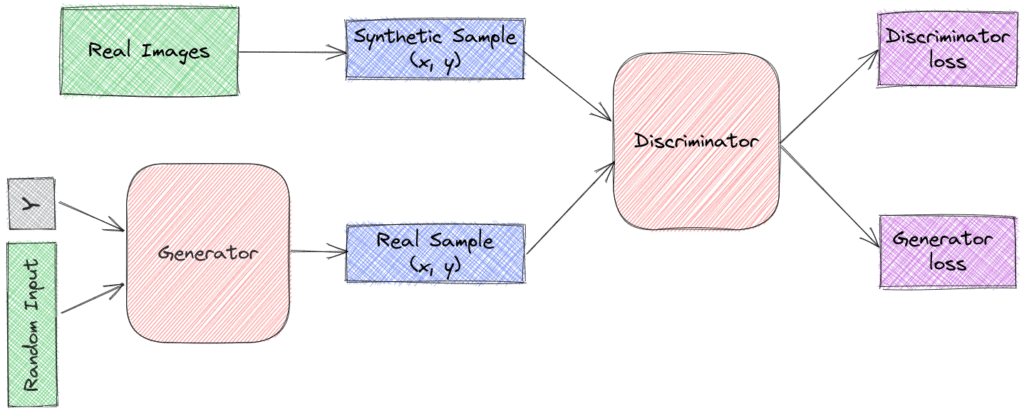
In conditional GANs, the generator is taught to generate examples of a specific class to fool the discriminator. In this way, a conditional GAN can generate samples from a domain of a given type. In the paper, we can see some examples of generated digits for each row conditioned to one label:

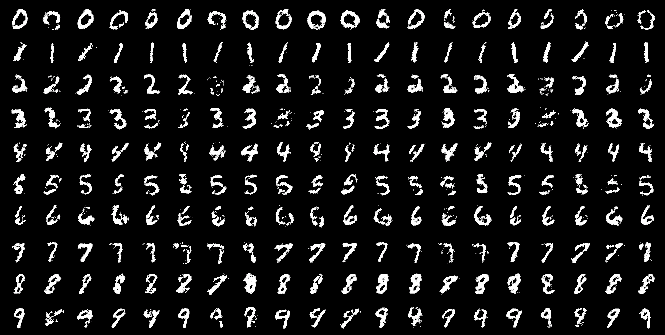
5. Limitations

The capabilities of GANs are impressive for data augmentation since they can effectively learn the underlying distribution of the input data and generate very realistic samples. However, there are some limitations:

1. We don’t have an intrinsic metric for evaluating the quality of the generated samples. Some experimental metrics have been proposed, but more research needs to be done towards that direction.
2. The training of GANs is usually unstable and requires a lot of computational resources.

6. Conclusion

In this article, we talked about how we can use GANs for data augmentation. First, we introduced the topics of data augmentation and generative models, and then we presented conditional GANs that can be used to generate very realistic samples. Finally, we highlighted some limitations of GANs.