How Is a Minimum Bottleneck Spanning Tree Different from a Minimum Spanning Tree?

1. Overview

In this tutorial, we’ll present two concepts from graph theory: minimum spanning tree and minimum bottleneck spanning tree. We’ll discuss the definitions with examples.

Finally, we’ll talk about the core differences between two tree structures.

2. Definition of Minimum Spanning Tree (MST)

Given an undirected, connected and weighted graph $G(V, E)$ . A spanning tree $\mathbf{S (V_1, E_1)}$ on the graph $\mathbf{G}$ is a tree that includes all the vertices of $\mathbf{G}$ . Hence, $V_1 = V$ . Additionally, all the edges in $S$ should also be present in $G$ . Therefore, $E_1 \subseteq E$ .

The spanning tree for an input graph is not unique. Moreover, for a given graph $G$ , we can find various spanning trees. The cost of a spanning tree is the sum of all the edges present in the tree. Hence, based on the edge weights, the cost of the spanning trees for a given graph can be different.

Now we’re ready to discuss the definition of minimum spanning tree. A minimum spanning tree is a spanning tree that has minimum cost among all possible spanning trees for a given graph.

A diverse range of real-life applications uses the minimum spanning tree such as image segmentation, recognition of the handwritings, face tracking in real-time (in a video), analysis of clusters, network design.

2.1. Example

Let’s see an example of how to find a minimum spanning tree from a graph $\mathbf{G_1}$ :

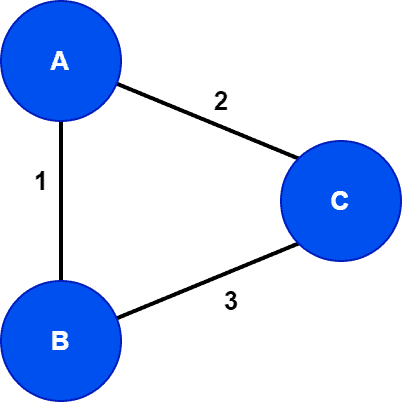
In this example, the input graph $G_1$ is a complete graph with $\mathsf{3}$ vertices. Next, let’s find all the possible spanning trees for the graph $G_1$ :

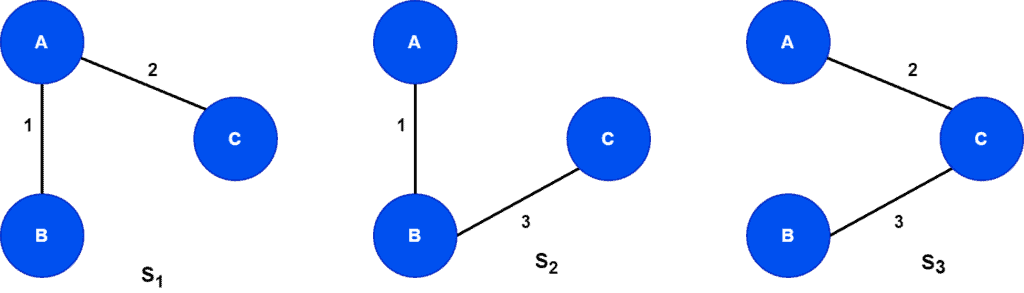
As the input graph, $G_1$ is fully connected, the total number of possible spanning trees is $N^{N - 2}$ . Here, $N$ denotes the total number of vertices in the graph. Therefore, we generated $\mathsf{3^{3 - 2} = 3}$ spanning trees for the graph $G_1$ .

The cost of spanning trees $S_1, S_2, S_3$ are $\mathsf{3, 4, 5}$ . Hence, we can see that among all the possible spanning trees of $G$ , $S_1$ has minimum cost. Therefore, $\mathbf{S_1}$ is the minimum spanning tree for the graph $\mathbf{G_1}$ .

3. Definition of Minimum Bottleneck Spanning Tree (MBST)

A bottleneck in a spanning tree is defined as the edge with maximum weight. Therefore, a minimum bottleneck spanning tree in an undirected, connected, and weighted graph $\mathbf{G(V, E)}$ is a tree whose maximum weighted edge is minimum among all the possible spanning trees of $\mathbf{G}$ .

As we already discussed, for a given graph, there might be several spanning trees. Therefore, we select a spanning tree with minimum cost as a minimum spanning tree from the set of spanning trees. In the minimum spanning tree, the edge with the maximum cost is a bottleneck edge. Finally, spanning trees that contain this particular edge are minimum bottleneck spanning trees.

3.1. Example

Let’s take an undirected, connected, and weighted graph $\mathbf{G_2}$ :

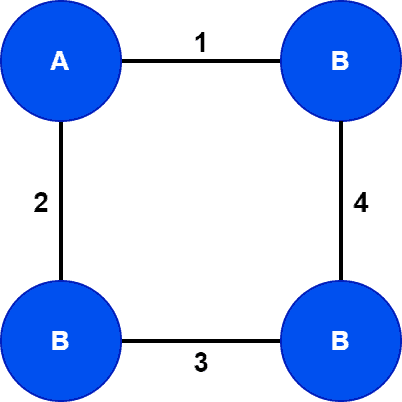
Now let’s list out all the spanning trees with cost and bottleneck edge:

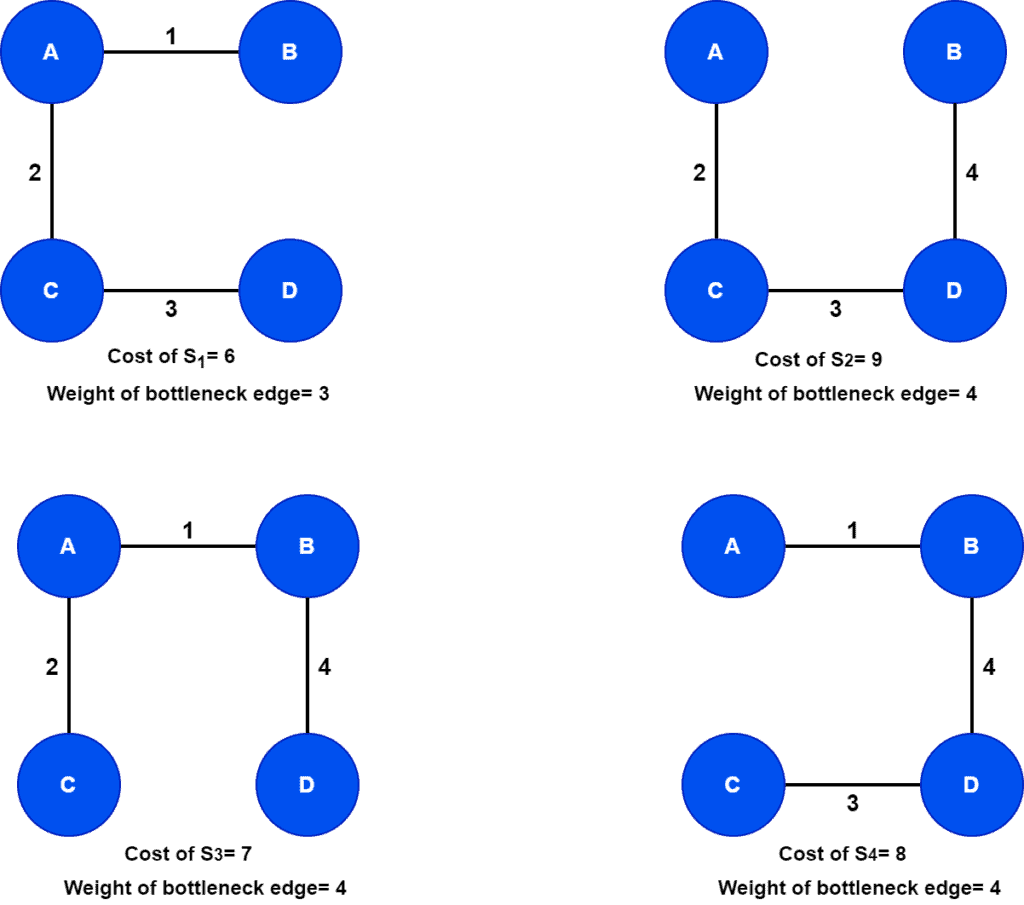
Here, the total number of spanning trees corresponding to the graph $G_2$ is $4$ . Finding all the possible spanning trees from the given graph is the first step of finding the minimum bottleneck spanning trees. The next step is to find the minimum spanning tree among all possible spanning trees.

Among all $4$ possible spanning trees of $G_2$ , $S_1$ has the minimum cost. Therefore, $S_1$ is a minimum spanning tree of $G_2$ . We need to find the bottleneck edge, the maximum weighted edge in the minimum spanning tree $S_1$ .

We can see the edge $(C, D)$ in $S_1$ is the bottleneck edge as its the highest weighted edge in $S_1$ . Hence, all the spanning trees that contain the edge $(C, D)$ are the minimum bottleneck spanning trees. Therefore, for graph $\mathbf{G_2}$ , the minimum bottleneck spanning trees are $\mathbf{S_1, S_2, S_4}$ .

3.2. Properties of MBST

A minimum bottleneck spanning tree has some interesting properties. A minimum bottleneck spanning tree may or may not be a minimum spanning tree. In the case of $G_2$ , we found $\mathsf{3}$ minimum bottleneck spanning trees. Out of $\mathsf{3}$ , $S_1$ is a minimum spanning tree. But $S_2$ and $S_3$ are not minimum spanning trees. Hence, not all the minimum bottleneck spanning trees are minimum spanning trees.

An MST is always an MBST. By the definition of an MBST, the bottleneck edge should belong to an MST. In fact, we select MBSTs from the spanning trees that contain the bottleneck edge.

The total weight of an MBST will always be greater than or equal to the total weight of an MST for a given graph. For example, the weight of the MST for the graph $G_2$ is $6$ . On the other hand, the weights of the MBSTs of $G_2$ are $6, 9,$ and $8$ .

4. Differences Between MBST and MST

Now we know how an MBST is different from an MST. Let’s talk about the core differences between them:

5. Conclusion

In this article, we discussed two very close yet different graph concepts in graph theory: minimum spanning tree, minimum bottleneck spanning tree. We presented the definition of both the trees with graph examples.

Finally, we discussed the core differences between them.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex