1. Overview
In this tutorial, we’ll present the decrease-key operation for the min heap-based priority queue.
First of all, we’ll review the usage and idea of min-heaps.
Next, we’ll implement the updates for the basic operations. After that, we’ll implement the decrease-key operation.
2. Min-Heap Background
2.1. Min-Heap Usage
The min-heap data structure is used to handle two types of operations:
- Insert a new key to the data structure. The time complexity of this operation is
, where 
is the number of keys inside the heap. - Extract the key with the minimum value from the data structure, and delete it. Similarly, the time complexity of this operation is also , where is the number of keys inside the heap.
In this tutorial, we’ll present a third operation called decrease-key, which allows us to decrease the value of a certain key inside the data structure. Mainly, the decrease-key operation is used in Dijkstra’s algorithm when we discover a new path to a certain node at a lower cost.
2.2. Min-Heap Data Structure
To begin with, the heap data structure is a complete binary tree. Therefore, the min-heap data structure is a complete binary tree, where each node has a smaller value than its children. Consequently, each node has a larger value than its parent.
Take a look at the example of a min-heap:
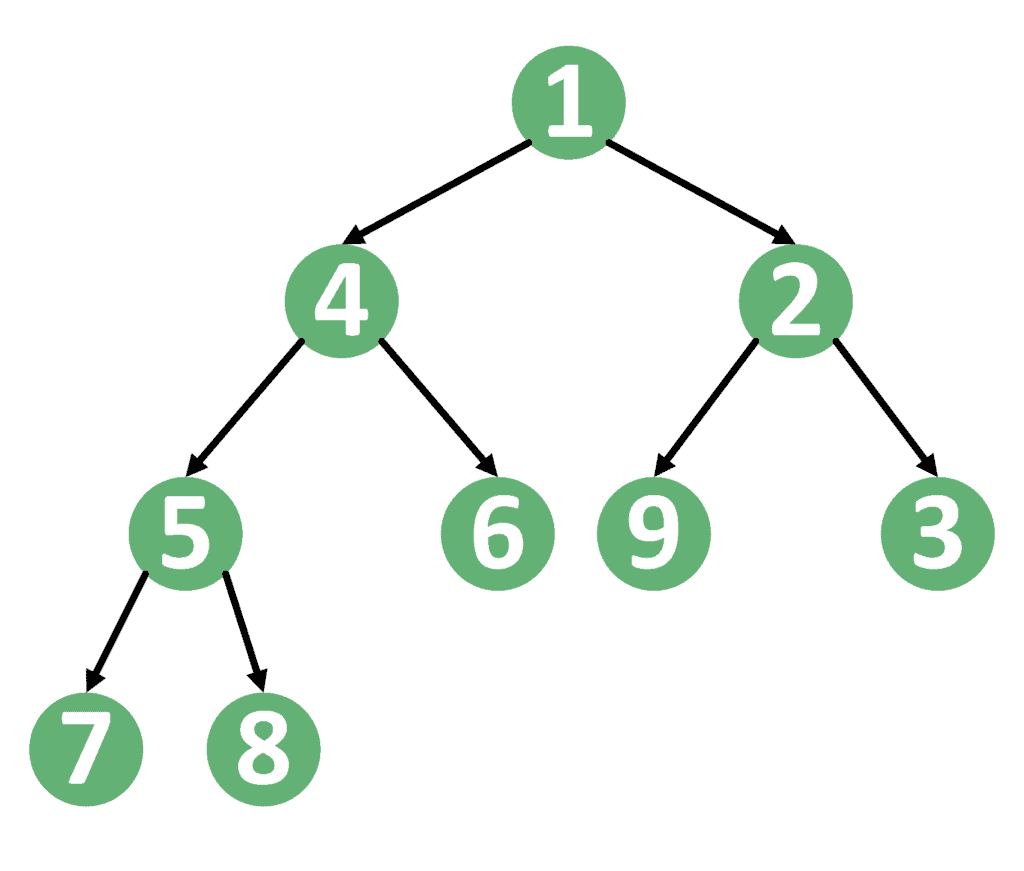
As we can see, each key is smaller than its children and larger than its parent. Therefore, the smallest value will always be the root of the tree. However, storing the heap data structure in a complete binary tree is complex. Hence, we use an array to store it.
First, we store the value of the root in index 1. Next, we store the left child in index 2 and the right child in index 3. Generally, if we stored a node in index 
, we store its left child in index 
and its right child in index 
.
Let’s take a look at storing the heap example we provided before:
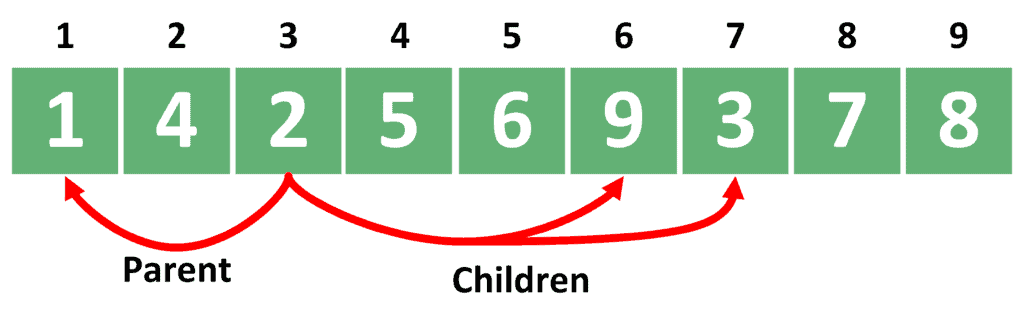
Note that the parent of the ith node will be in index 
. Please note that the index of the parent is obtained by dividing the index of the node by 2, discarding the modulo of the division.
For example, we stored the node with value 2 in index 3. Therefore, we stored its left child with value 9 in index 
. Also, we stored its right child with value 3 in index 
. In addition, we stored the parent, which is the root in this case, in index 
.
3. Needed Updates
To decrease the value of a certain key inside the min-heap, we need to reach this key first. In ordinary heaps, we can’t search for a specific key inside the heap.
Therefore, we’ll keep a map data structure beside the original array. This map will store the index of each key inside the heap. Hence, when we need to access a certain key inside the heap, we’ll use this map to determine its index.
Let’s discuss the needed updates to the basic heap operations.
3.1. Swap
When we insert or extract a value from the heap, we usually perform a series of swaps. The reason for these swaps is to put a key to its correct place, as we’ll see later.
Let’s implement a swap function that takes two indices of the array and swaps their values:
Firstly, we swap the values inside indices and 
. Secondly, we update the indices of these values inside the map. This function could be implemented in 
time complexity if we used a hash map.
3.2. Insert
When inserting a new key to the min-heap, we need to maintain the idea of it being a complete tree. Therefore, we’ll insert the key at the end of the array. After that, we’ll keep moving the key up as much as needed.
Take a look at the updated insert operation:
In the beginning, we insert the new key at the end of the array. Next, we store the index of this key inside the map.
After that, we perform multiple steps starting from the inserted key. In each step, we compare the value of the key with the value of its parent. If this key has a smaller value than its parent, then we swap their values using the function in algorithm 1. These steps continue until we either reach the root, or the key becomes smaller than its parent.
The complexity of the insert operation stays as before, where is the number of keys inside the heap.
3.3. Extract
When extracting a key from a heap, we also need to maintain the idea of it being a complete binary tree. Therefore, we put the last key inside the heap in place of the root. After that, we keep moving this key down as much as needed.
Let’s have a look at the extract operation:
Firstly, we store the value to be returned and remove it from the map. Next, to keep the heap complete, we put the last key in the root’s place and update its index inside the map.
After that, we perform multiple steps starting from the root. In each step, we compare the value of the key with the value of the minimum between its children. If the value of the key is larger than the minimum of its children, we swap these two keys using the function in algorithm 1. Otherwise, we break the while loop.
Finally, we return the value we stored in the beginning.
The complexity of the extract operation stays as before, where is the number of keys inside the heap.
4. Decrease-Key
To decrease the value of a certain key, we’ll use the map to locate its index. After we locate its index, we’ll change its value, and start moving it up the tree if needed. The reason we’re moving the key up the tree is that its value got reduced. Therefore, it’ll either stay in its place or move up.
Let’s examine the decrease-key operation:
Firstly, we locate the index of the given key using the map. Secondly, we remove the old value of the key from the map, decrease it, and store the new value inside the map.
Thirdly, we perform multiple steps starting from the index of the key. In each step, we compare the value of the key with the value of its parent. If the value of the key is smaller than the value of its parent, we swap their values using the function in algorithm 1.
Once we reach the root or reach a place where the value of the parent is smaller than the value of the key, we break the while loop.
The complexity of the decrease operation is , where is the number of keys inside the heap.
5. Conclusion
In this tutorial, we presented the decrease-key operation for min-heaps. Firstly, we explained the basic concepts of a min-heap. Secondly, we discussed the needed updates for the basic operations.
Thirdly, we implemented the decrease-key operation.