Yes, we're now running our Black Friday Sale. All Access and Pro are 33% off until 2nd December, 2025:
How Do Merkle Trees Work?
Last updated: March 18, 2024
1. Introduction.
In this tutorial, we’re going to have a look at Merkle Trees. We’ll see how we can construct them and a couple of ways to use them.
2. What Is a Merkle Tree?
Merkle Trees, or Hash Trees, is a construct used for generating hashes of large amounts of data. This works whether it’s a single large file, a lot of small files, or any scenario where we have a significant amount of data.
A Merkle Tree is a tree of hash values. The end result of this is a tree structure in which every intermediate node is a hash of its child nodes until the leaf nodes of the tree are actually hashes of the original data. This means every leaf node is a hash of only a small portion of the data.
These data structures have two major purposes:
- Efficiently verifying that a large amount of data is unchanged and finding exactly where any changes may have occurred
- Efficiently proving that a piece of data is present in a larger data set
We’ll see how to achieve these later.
Using a hash function for generating each of these nodes has some benefits. Hashes typically have a fixed size, regardless of the amount of input data. This means that a Merkle Tree with a known number of leaf nodes will have a known size, regardless of the actual size of the data being hashed. Good hash functions are also generally collision resistant. This means that it’s hard to change the original data and still get the same hashes out, which means that we can rely on it to verify the data.
These have a wide range of uses in software, from various file systems such as Btrfs and ZFS, data transfer protocols such as IPFS, database engines such as Cassandra and Riak, and even blockchain implementations such as Bitcoin and Ethereum.
3. Constructing a Merkle Tree
So, how do we construct a Merkle Tree? We start by splitting our data into blocks. The leaf nodes of our tree are then the hashes of these blocks. We then calculate all of the other nodes in our tree by combining their immediate branches and generating a hash of them:
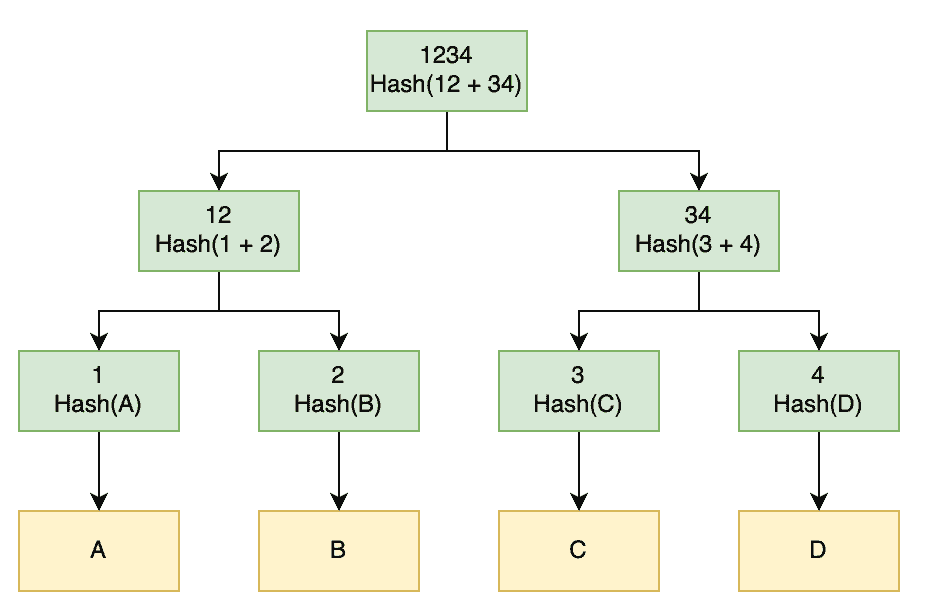
Here we have 4 data blocks – “A”, “B”, “C”, and “D”. The first thing that we do is hash each of these into hashes “1”, “2”, “3”, and “4”. Next, we combine and hash these. So we’ll generate hash “12” by combining hashes “1” and “2” and then hashing this result. We repeat this all the way up the tree until we have our root node.
Exactly how we determine the data blocks isn’t important as long as it’s reproducible. If we were generating this for a single huge piece of data, we might split it into equal-sized pieces. For example, we could split a 1GB file into 64 blocks that are each 16MB large. Alternatively, if we were generating this for a large collection of data, then we might have each one be a block. For example, we might split a directory of files so that each block represents a single file.
It’s also not important which hash function we use, nor how we combine previous hashes before generating the next level of hashes. The only thing that is important is that it’s exactly the same both when creating and using the Merkle Tree.
4. Verifying Data Integrity
Merkle Trees can be an efficient way to verify the integrity of large quantities of data. The naive way of doing this is to simply generate the same tree and then compare the top hash from this to the top hash from the original data. If they match, then the entire data is a match, and if they differ, then there is some inconsistency in the data.
However, we can do better than this. If we can obtain the entire Merkle Tree from the original data, then we can verify the integrity of the data and also pinpoint exactly where any changes might have occurred. For example:
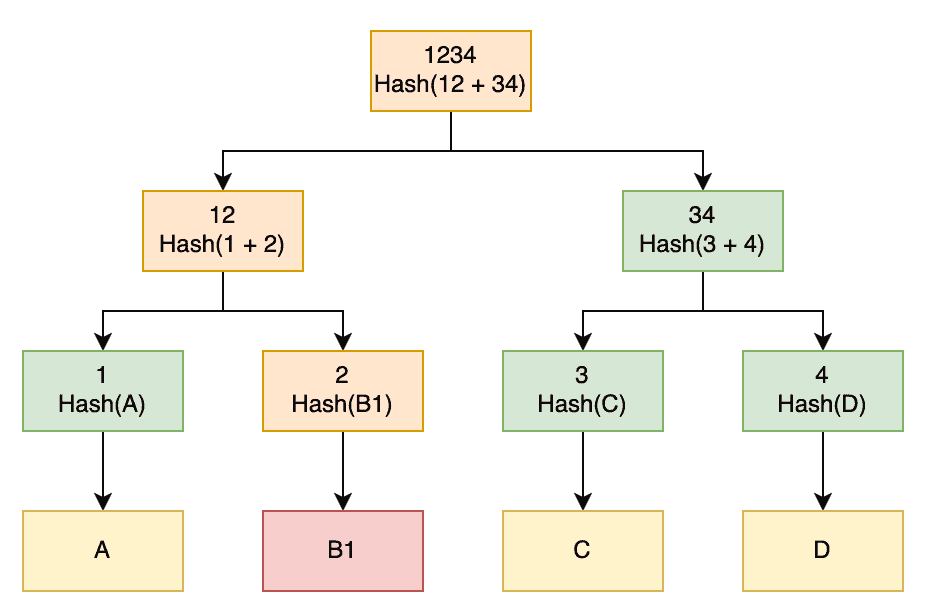
Here we have downloaded the exact same file as before, but block “B” was somehow corrupted. When we generate the top hashes for this new file, we will see that it differs from that of the original file, which tells us that something is wrong.
Given this, we can then compare the next level of the tree. Here we will see that node “12” differs between the two trees, but “34” is the same. This tells us that everything on the “34” side of the tree is good – which means we know data blocks “C” and “D” are correct – and instead, something is wrong on the “12” side of the tree.
Again, we now compare the next level of this subtree. Here we see that node “1” is the same, but node “2” is different. This tells us that data block “A” is correct, but data block “B1” is somehow different to what was in the original file.
We have now determined, from the original data blocks, exactly which of them are corrupted. This means that we can re-download only these blocks and replace them, and now we have the correct data. If we only had the top hash, we’d be forced to download the entire file again because we wouldn’t know exactly where the corruption was.
The deeper our tree is, the more hashes we need to compute to get to this point, but fewer data we’d need to download to fix it. This is beneficial since processing I/O is typically more efficient than network I/O. For example, if there were a single corrupted 16MB block in a 1GB file, then we’d have computed 127 hashes to save transferring an additional 1,008MB of data.
4.1. Untrusted Sources
As an additional bonus, because the entire Merkle Tree is hashed, as long as we have a trusted source for the top hash, we can obtain the entire tree from an untrusted source and still prove that it’s correct. For example, if we’re downloading files from a peer-to-peer network, we can get the top hash from a trusted source and actually download the Merkle Tree from the network itself. We can’t trust this as a source, but as long as we can trust the top hash, we can prove it’s correct.
As long as our hashes are resistant enough to collision attacks, it would be difficult for an untrusted source to produce a different tree with the same top hash. This means that we can download the tree from an untrusted source and then generate all of the appropriate hashes ourselves and check that they match. As long as doing this produces the same top hash, we know that every other hash in the tree is also correct. And if it doesn’t produce the same top hash, we can discard it and try again from a different source.
5. Proving Data Presence
Another use for Merkle Trees is to efficiently prove that a piece of data is present in the original set. For example, to prove that one particular file was present in a larger set of files or transactions within a blockchain.
We can do this using the exact opposite technique of verifying the data integrity. We provide all of the hashes at the top of opposite subtrees in the Merkle Tree, which can then be combined to demonstrate that they produce the same top hash:
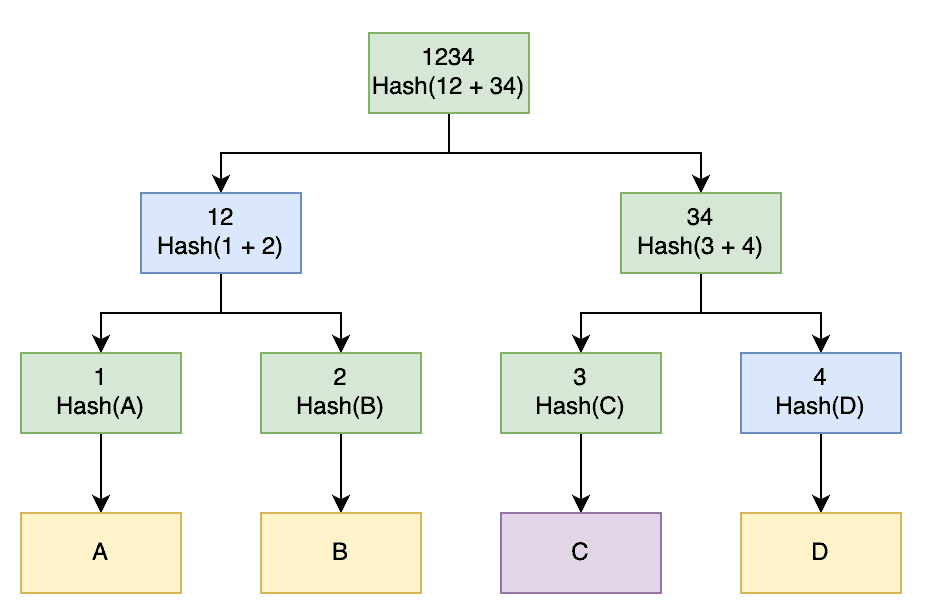
To prove that we have block C, we would provide the hash for this block and hashes “4” and “12”. The other system can then combine our hash for block C with the provided hash “4” to produce hash “34”, then combine this with hash “12” to produce hash “1234”. If this matches, we have successfully proven that we have block C.
As before, the deeper the tree, the more hashes we need, but the more fine-grained this can be. With our tree here, we need to provide 2 additional hashes and can confirm a block that is 1/4 of the original data set. If we had a tree of depth 6, then we would need to provide 5 additional hashes and can confirm a block that is 1/64 of the original data set.
The benefit here is that we can prove this to another party that only has access to the top hash, as opposed to only being able to prove it to other parties that have access to the original data. This can be significantly more efficient when the original data is very large or untrusted communication mediums are involved.
6. Conclusion
In this article we’ve seen exactly what a Merkle Tree is, how to construct one and how to use it for data validation and proving the presence of data.