Algorithm for Merging Two Max Heaps

1. Overview

In this tutorial, we’ll talk about the problem of merging two max binary heaps.

First, we’ll define the problem and provide an example to explain it. Then, we’ll present a solution for this problem and work through its implementation and time complexity.

2. Defining the Problem

Suppose we have two max binary heaps and , and we want to merge them into a single max heap . Recall the max binary heap is a binary tree where each node in this tree has a value greater than all the nodes’ values in its subtree.

Let’s take a look at the following example for a better understanding, Given two max binary heaps and in array representation. Recall we can represent a binary tree in an array format where the node with index has its left and right children located on and respectively:

• :
• :

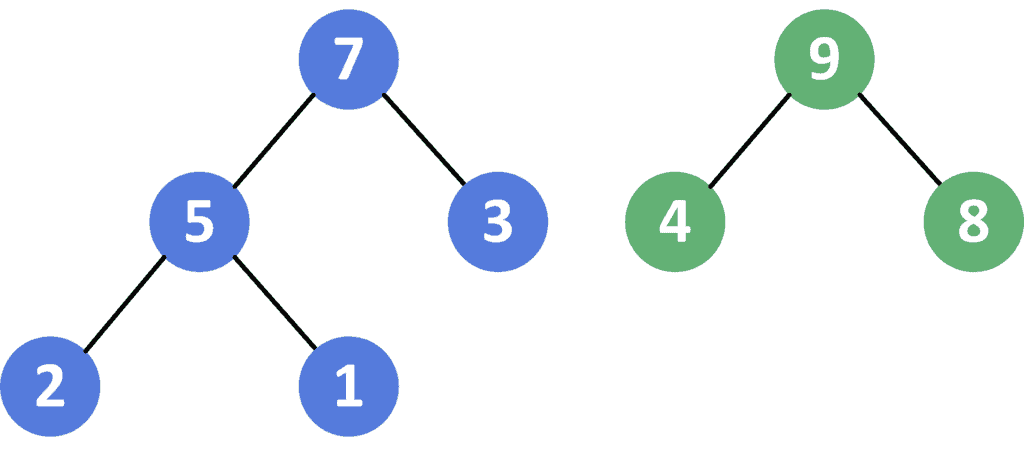
After merging these two max binary heaps, we’ll get the following one:

3. Solution

3.1. Main Idea

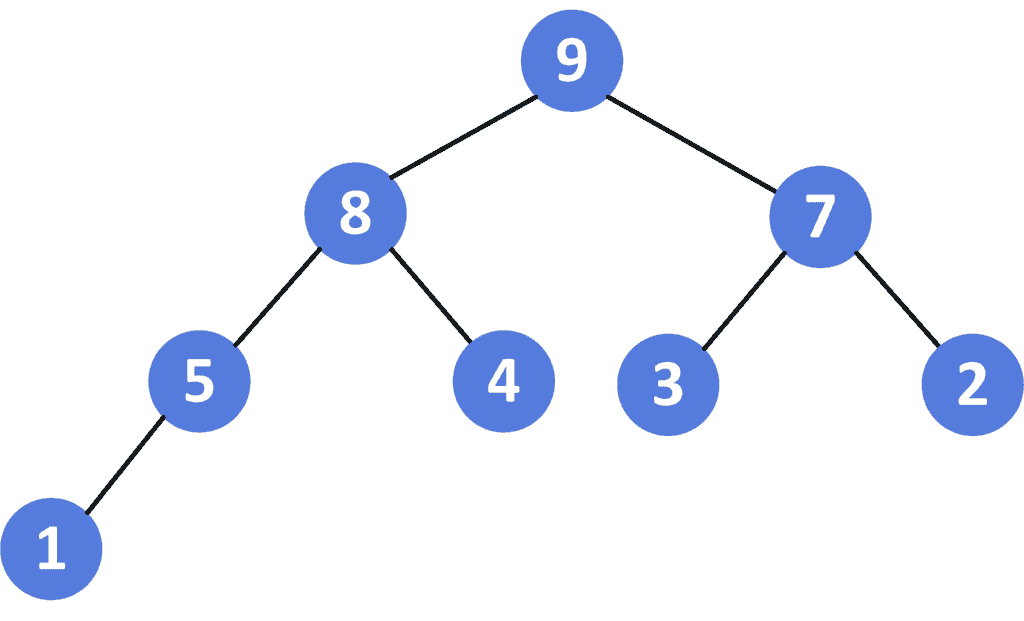
The main idea is to merge the array representation of the given max binary heaps; then we build the new max heap from the merged array.

First, we fix one of the given max heaps as a solution. Then, we’ll append the elements of the other max heap to it. Second, we’ll build a max heap on the merged array.

Finally, the max heap will be the merged version of the two given max heaps.

3.2. Max Heapify

Let’s take a look at the implementation of the algorithm:

algorithm MaxHeapify(H, pos):
    // INPUT
    //    H = The heap as an array
    //    pos = The position in H to start the heapify process
    // OUTPUT
    //    Adjusts the subtree rooted at pos to satisfy the max heap property
    
    left <- 2 * pos + 1
    right <- 2 * pos + 2
    
    max <- pos
    
    // Check left child
    if left < H.size and H[left] > H[max]:
        max <- left
    
    // Check right child
    if right < H.size and H[right] > H[max]:
        max <- right
    
    // If max is not the current position, swap and continue heapifying
    if max != pos:
        Swap(H[max], H[pos])
        MaxHeapify(H, max)

Initially, we have the recursive function that will rearrange the elements of a given array to make the heap valid. The function will have two parameters: the array of the heap we want to build and the current position .

First, we declare and children of the current node, which will be equal to and respectively. Then, we’ll declare , which represents the index of the node that has the maximum value.

Second, we check if there’s a node. If there’s one and its value exceeds the current max node, we update the to equal . Also, we do the same for the child.

Finally, we check if isn’t equal to the current , which means there’s a child of node with a value greater than its value. If so, we swap them to make the heap valid and call our function to the new to check if it’s still valid.

3.3. Algorithm

Let’s take a look at the implementation of the algorithm:

algorithm MergeHeaps(H1, H2):
    // INPUT
    //    H1 = First max heap as an array
    //    H2 = Second max heap as an array
    // OUTPUT
    //    A new max heap containing all the elements from H1 and H2
    
    merged_heap <- H1
    
    for node in H2:
        add node to merged_heap
    
    // Heapify from the last non-leaf node down to the root node
    for i <- merged_heap.size - 1 down to 0:
        MaxHeapify(merged_heap, i)
    
    return merged_heap

Initially, we have the function that will return the merged max heap from the given two max heaps. The function will have two parameters, the first and the second max heaps.

First, we declare that will store the array representation of the merged version of the given max heap. Initially, it’s equal to the first max heap .

Second, we iterate over the elements of the second max heap’s array and append each element to the .

Third, we iterate over the nodes of the current heap in bottom-up order and call to fix the invalid nodes that don’t meet the definition of max heap.

Finally, we return the .

3.4. Complexity

The time complexity of this approach is , where is the number of vertices of the first heap , and is the number of vertices of the second heap . The reason behind this complexity is the same as the complexity of building a max heap.

The space complexity here is . since we’re storing the vertices of the new heap.

4. Conclusion

In this article, we discussed the problem of merging two max binary heaps. We defined the problem and provided an example to explain it.

Finally, we provided a simple approach to solve it and walked through its implementation and time complexity.