Maximum Value of an Integer: Java vs C vs Python

1. Introduction

In Data Science, when we talk about integers, we’re referring to a data type that represents some range of mathematical integers. We know that mathematical integers don’t have an upper bound, but this could be a problem in terms of memory size, forcing almost every computer architecture to limit this data type.

So, that’s the question we’re trying to ask today: “What’s the maximum integer value we can represent on a certain machine?”

2. Problem Explanation

Well, there isn’t a unique answer to this question since there are many factors that influence the answer. The main ones are:

• Platform bits
• Language used
• Signed or Unsigned versions

In computer science, the most common representation of integers is by a group of binary digits (bits), stored as a binary numeral system. The order of memory bytes varies – with bits, we can encode integers.

We can see the differences in this simple example: with bits, we can encode integers from to or from to .

Usually, the integer size is defined by the machine architecture, but some computer languages also define integer sizes independently. Different CPUs support different data types, based on their own platform. Typically, all support both signed and unsigned types, but only of a limited and fixed set of widths, usually 8, 16, 32 and 64 bits.

Some languages define two or more kinds of integer data types, one smaller to preserve memory and take less storage, and a bigger one to improve the supported range.

Another thing to keep in mind is the Word Size (also called Word Length) of the platform.

In computer science, a word is the unit of data used by a particular processor design, a fixed-sized piece of data handled as a unit by the hardware of the processor. When we talk about word size, we refer to the number of bits in a word and this is a crucial characteristic of any specific computer architecture and processor design.

Current architectures typically have a 64-bit word size, but there are also some with 32 bits.

3. Time for the Answers

In this section, we’ll answer our questions starting from the old friend C to the relatively new Python, passing through the evergreen Java. Let’s start.

3.1. C

The C language was designed in 1972, with the purpose of working the same way on different machine types. So, it doesn’t determine directly a range for the integer data type as that depends on machine architecture.

However, C has two kinds of integers; short and long.

A short integer is, at least, 16 bits. So, on a 16-bit machine, it coincides with the long integer format. The short integer format ranges from -32,767 to 32,767 for the signed version and from 0 to 65,535 for the unsigned. Well, it’s weird, but it seems that for the signed version we miss a number. That it’s easy to explain: because we need one bit for the sign!

If we run on a 64-bit system, we can easily calculate that the long format can reach a value, which corresponds to 18,446,744,073,709,551,615 for the unsigned data type and ranges from -9,223,372,036,854,775,807 to 9,223,372,036,854,775,807 in the signed version.

For completeness, we’ll take a little ride on the long long integer data type. The long long format is not available on C, but only on the C99 version. It has double the memory capacity of a long data type, but it’s obviously not supported by compilers that require the previous C standard. With the long long data type, we can reach a huge if we’re running it on a 32-bit machine or higher.

3.2. Java

Talking about Java, we must remember that it works through a virtual machine. That saves us from all the variability explained for the C language.

Java supports only signed versions of integers. They are:

• byte (8 bits)
• short (16 bits)
• int (32 bits)
• long (64 bits)

So, with the long integer format we can reach  as with C on a 64-bit machine but, this time, on every machine architecture.

However, with some bit manipulation, we can get unsigned versions, thanks to the char format. That’s a 16-bit format, so the unsigned integer format can reach 65,535.

But with Java, we can go further with a little hack so we can represent very large integer numbers through the BigInteger class library. This library combines arrays of smaller variables to build up huge numbers. The only limit is the physical memory, so we can represent a huge, but still limited, range of integers.

For example, with 1 kilobyte of memory, we can reach integers up to 2,466 digits long!

3.3. Python

Python directly supports arbitrary precision integers, also called infinite precision integers or bignums, as a top-level construct.

This means, as with Java BigInteger, we use as much memory as needed for an arbitrarily big integer. So, in terms of programming language, this question doesn’t apply at all for Python, cause the plain integer type is, theoretically unbounded.

What is not unbounded is the current interpreter’s word size, which is the same as the machine’s word size in most cases. That information is available in Python as sys.maxsize, and it’s the size of the largest possible list or in-memory sequence, which corresponds to the maximum value representable by a signed word.

On a 64-bit machine, it corresponds to = 9,223,372,036,854,775,807.

4. Flowchart

Let’s take a look at a flowchart to summarize what we’ve seen so far:

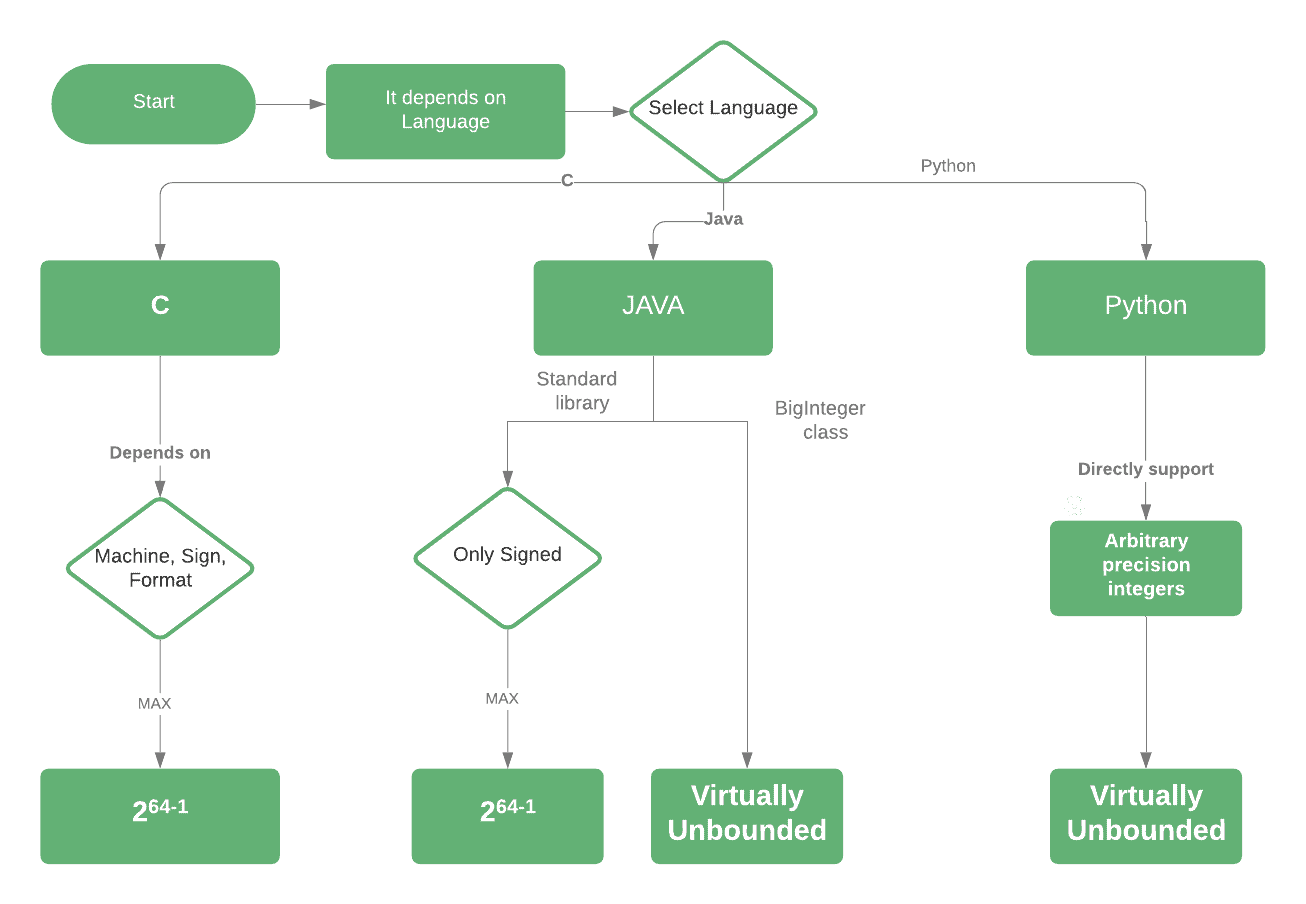
5. Real Code for Each Language

Here’s some real code to directly check what we’ve discussed so far. The code will demonstrate the maximum and minimum values of integers in each language.

Since those values don’t exist on Python, the code shows how to display the current interpreter’s word size.

5.1. C Code

#include<bits/stdc++.h>
int main() { 
    printf("%d\n", INT_MAX); 
    printf("%d", INT_MIN); 
    return 0; 
}

5.2. Java Code

public class Test {
    public static void main(String[] args) {
       System.out.println(Integer.MIN_VALUE);
       System.out.println(Integer.MAX_VALUE);
    }
}

5.3. Python Code

import platform
platform.architecture()
import sys
sys.maxsize

6. Conclusion

In this article, we covered the differences between these three top languages about the maximum possible integer. We also showed how this question doesn’t apply in some situations.

However one should always use the best fitting in his situation to prevent memory consumption and system lag.