Representing Max Heap in an Array

1. Introduction

In this tutorial, we’ll show how to represent the Max Heap data structure in an array. It’s a very handy alternative to the explicit binary tree representation.

2. Overview of the Representation

The array representation of Max Heap consists of the following data:

• Array to hold the values of Max Heap
• Integer index keeping the last element’s index in the array. If is , Max Heap is empty

For convenience, we’ll assume the array is 1-indexed. We keep Max Heap’s root element at . Then, we keep the root’s children at and at . The general recursive process defining the order of Max Heap’s elements in the array is:

• The root element is at index 1
• For any node at index , its left child is at index
• For any node at index , its right child is at index

With the rules above, we can deduce that for any node at index , its parent is at index . The division is with floor rounding.

Below is a sample Max Heap:

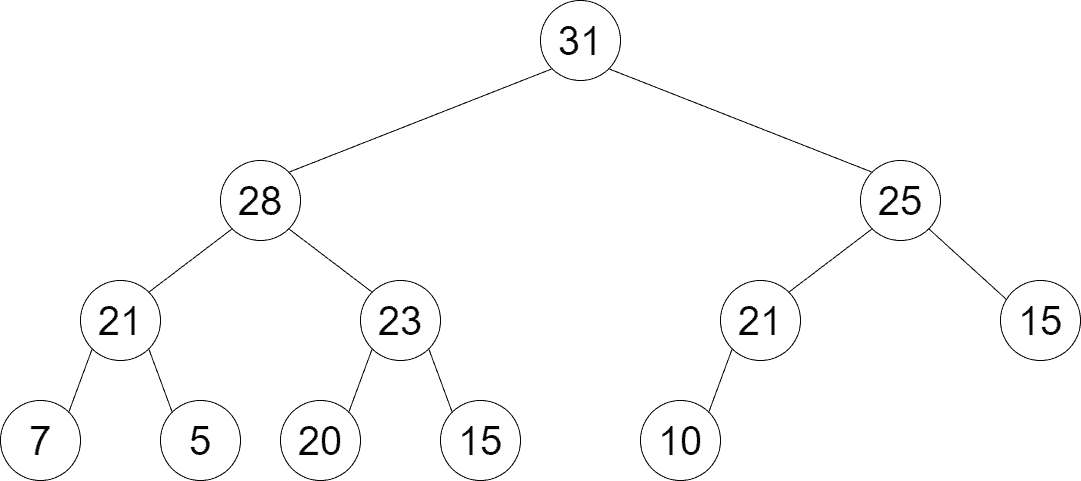
Let’s color the node levels in the Max Heap. There’re 4 levels:

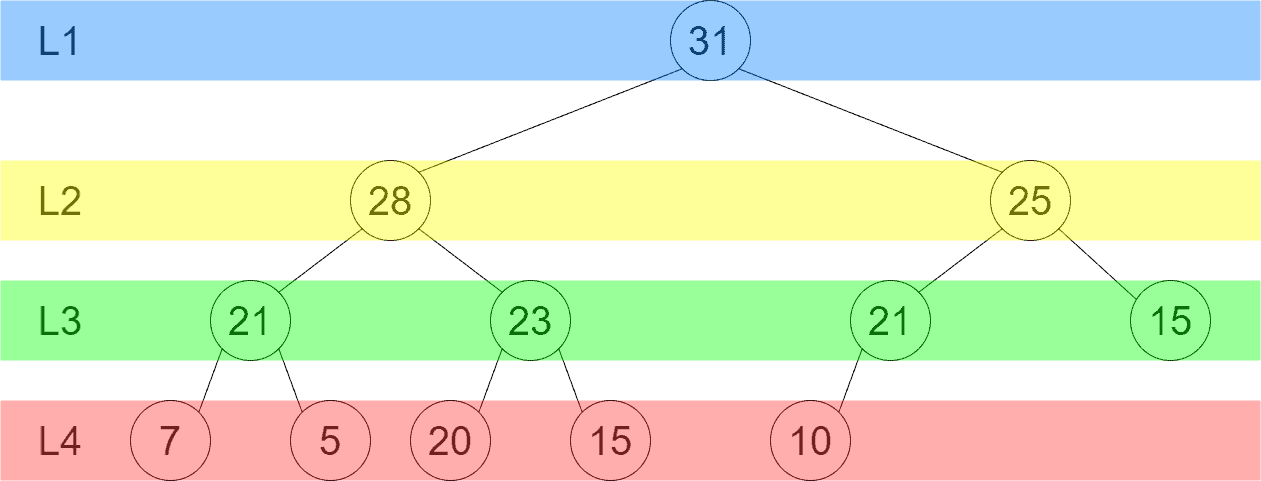
Now we’ll use the ordering principle defined above to put the Max Heap elements into an array. The resulting array is:

As we can see, our element ordering is equivalent to putting Max Heap nodes into the array level by level. We start from the uppermost level and end with the lowermost one. And at each level, nodes are processed from left to right.

3. Max Heap Operations and Pseudocode

Max Heap is a data structure supporting fast retrieval of maximum. Thus, it’s enough for it to support a few operations. Basically, it needs to support element addition, maximum element retrieval, and maximum element removal. Additionally, the array representation needs to have the operation of building Max Heap from an array – the heapify operation.

3.1. Insertion

For the traditional representation of Max Heap as a binary tree, insertion adds a new element to the lowest layer. At the lowest layer, the elements are added from left to right in order to preserve the property of a complete binary tree.

Similarly, for the array representation, a new element is added to the end of the array. Subsequently, the added element needs to travel left to the beginning of the array by swapping with smaller parents. This way, the Max Heap invariant is preserved, and the element finds the right place to reside in the array. It’s equivalent to how new elements bubble up in the tree until they find the right place in the tree representation of Max Heap.

Let’s jump to the pseudocode:

algorithm INSERT(H, value):
    // INPUT
    //    H = a max heap
    //    value = the value to insert into H
    // OUTPUT
    //    value is added to H, maintaining the max heap property
    
    H.tail <- H.tail + 1
    H.elements[H.tail] <- value
    
    child <- H.tail
    parent <- child / 2
    
    while parent >= 1 and H.elements[parent] < H.elements[child]:
        SWAP(H.elements[parent], H.elements[child])
        child <- parent
        parent <- child / 2

3.2. Maximum Retrieval

Maximum is always the first element of the array. Note that sometimes there’s a need to retrieve the maximum without its removal from the Max Heap. That’s why we provide two separate operations for maximum retrieval and removal. The pseudocode of the operation is given below:

algorithm MAX(H):
    // INPUT
    //    H = a max heap
    // OUTPUT
    //    Returns the maximal element of H
    
    if H.tail = 0:
        return null
    
    return H.elements[1]

3.3. Maximum Removal

When we remove the maximum, the tail element jumps to the beginning of the array. Then, the tail pointer is decremented. Finally, the first element (the tail element before removal) travels right to the end of the array by swapping with children that are greater.

Let’s see the pseudocode:

algorithm REMOVE(H):
    // INPUT
    //    H = a max heap
    // OUTPUT
    //    The maximum element of H is removed
    
    if H.tail = 0:
        return
    
    H.elements[1] <- H.elements[H.tail]
    H.tail <- H.tail - 1
    
    parent <- 1
    maxChild <- index of parents maximum child or infinity if it has no children
    
    while maxChild <= H.tail and H.elements[parent] < H.elements[maxChild]:
        SWAP(H.elements[parent], H.elements[maxChild])
        parent <- maxChild
        maxChild <- index of parents maximum child or infinity if it has no children

3.4. Heapify

For the binary tree representation of Max Heap, heapify builds the Max Heap bottom up. Leaf nodes satisfy the Max Heap invariant, so it starts building Max Heap from the nodes that have children. These nodes are situated at the level above the lowest. And as Max Heap is a complete binary tree, the leaf nodes make up approximately half of all the nodes.

Similarly, for the array representation of Max Heap, heapify omits the right half of the array. It builds the Max Heap from right to left, starting from the middle of the array. When it processes the current element, it considers that the subarray to the right is already heapified. Thus, heapify needs to check if the current element can be included in the Max Heap structure as-is or if it needs to be swapped with its children until it finds its correct place.

The pseudocode for heapify is given below:

algorithm HEAPIFY(A):
    // INPUT
    //    A = an array to heapify
    // OUTPUT
    //    A max heap H corresponding to array A

    start <- A.size / 2
    for i <- start, start - 1, ..., 1:
        parent <- i
        maxChild <- index of the maximum child of i or infinity if it has no children
        while maxChild <= A.size and A[parent] < A[maxChild]:
            SWAP(A[parent], A[maxChild])
            parent <- maxChild
            maxChild <- index of the maximum child of i 
                        or infinity if it has no children
    
    H <- an empty heap
    H.elements <- A
    H.tail <- H.elements.size
    
    return H

4. Conclusion

In this tutorial, we’ve discussed how to use an array for Max Heap representation. It’s a concise way of implementing Max Heap with a minimum amount of code.