Matrix Chain Multiplication Using Dynamic Programming

1. Introduction

In this tutorial, we’ll show how to multiply a matrix chain using dynamic programming. This problem frequently arises in image processing and computer graphics, e.g., animations and projections.

2. Matrix Chains

Let’s start with an example. We have four matrices: $A, B, C$ and $D$ . Their shapes are $(4,5)$ , $(5,3)$ , $(3,10)$ , and $(10,2)$ , respectively.

Since each matrix’s number of columns corresponds to the next one’s number of rows, their product $A \times B \times C \times D$ is defined.

We can calculate it sequentially. First, we multiply $A$ and $B$ to get an intermediate $(4, 3)$ -matrix $M_1$ . Then, we multiply $M_1$ with $C$ and get a $(4, 10)$ -matrix $M_2$ . Finally, we get the result by multiplying $M_2$ with $D$ :

$\overbrace{(\underbrace{\text(A \times B)}_{M_1} \times C)}^{M_2} \times D$

How many operations do we perform this way?

To multiply two matrices $U$ and $V$ of shapes $(p, q)$ and $(q, r)$ , we must compute $p r$ elements. For each, we perform $q$ scalar multiplications and $q-1$ additions. So, the total number of operations, $cost(U \times V)$ , is $p r (2q -1)$ .

In our example:

$\begin{aligned} cost(A \times B) & = 4 \cdot 3 \cdot (2 \cdot 5 - 1) = 108 \\ cost(M_1 \times C) &= 4 \cdot 10 \cdot (2 \cdot 3 - 1) = 200 \\ cost(M_2 \times D) &= 4 \cdot 2 \cdot (2 \cdot 10 - 1) = 152 \end{aligned}$

That’s 460 operations. However, since matrix multiplication is associative, we can compute the chain in a different order:

$A \times \overbrace{(B \times \underbrace{(C \times D)}_{M_1'})}^{M_2'}$

This multiplication order involves 236 operations:

$\begin{aligned} cost(C \times D) & = 3 \cdot 2 \cdot (2 \cdot 10 - 1) = 114 \\ cost(B \times M_1') &= 5 \cdot 2 \cdot (2 \cdot 3 - 1) = 50 \\ cost(A \times M_2') &= 4 \cdot 2 \cdot (2 \cdot 5 - 1) = 72 \end{aligned}$

The reduction is almost 50%.

2.1. Formulation

So, in problems of this type, we have $n$ matrices $A_1, A_2, \ldots, A_n$ of the shapes $(p_1, q_1), (p_2, q_2), \ldots, (p_n, q_n)$ such that $q_i = p_{i+1}$ for all $i=1,2,\ldots, n-1$ .

The goal is to find the multiplication order that minimizes $\boldsymbol{cost(A_1 \times A_2 \times \ldots \times A_n)}$ , the number of scalar multiplications and additions in computing the product $\boldsymbol{A_1 \times A_2 \times \ldots \times A_n}$ .

3. Dynamic Programming

We can use dynamic programming to do this. So, let’s start with the recursive relation.

3.1. Recursion

Let $cost(i, j) = cost(A_i \times A_{i+1} \times \ldots \times A_{j})$ (where $1 \leq i \leq j \leq n$ ). No matter how we order multiplications, the final product will always result from multiplying two matrices.

So, we compute $\boldsymbol{A_i \times \ldots \times A_j}$ by splitting it into the “left” and “right” products $A_i \times \ldots \times A_k$ (of shape $(p_i, q_k)$ ) and $A_{k+1} \times \ldots \times A_j$ (of shape $(p_{k+1}, q_j)$ ):

$(A_i \times \ldots \times A_k ) \times ( A_{k+1} \times \ldots \times A_j)$

The choice of $k$ determines the cost:

$cost(i, k) + cosr(k+1, j) + p_i q_j (2 p_{k+1} - 1)$

Therefore, we should choose the $k$ that minimizes the number of operations:

$cost(i, j) = \begin{cases} \min_{k=i}^{j-1} \left\{cost(i, k) + cost(k+1, j) + p_i q_j (2 p_{k+1} - 1)\right\}, & j > i \\ 0, & j=i \end{cases}$

The base case is $j=i$ , and its cost is zero because we don’t perform any operation to compute $A_i$ .

3.2. Tabular Algorithm

Let’s check out the tabular approach to computing $cost(1, n)$ .

In this method, we start from the base cases and work up to $cost(1, n)$ one diagonal at a time. So, after the base cases on the main diagonal, we compute the costs $cost(i, i+1)$ for $i=1,2,\ldots, n-1$ of multiplying pairs:

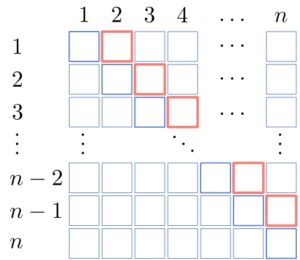
The first iteration of the tabular approach.

Then, we compute the $cost(i, i+2)$ for $i=1,2,\ldots, n-2$ :

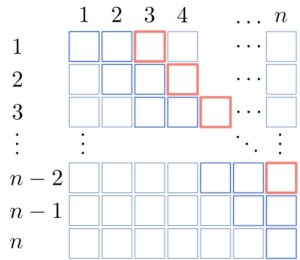
The second iteration of the tabular approach

Continuing this way, we calculate $cost(1, n)$ in the end:

We keep track of the splitting indices by storing them in a separate data structure $T$ as we compute the costs.

We can use $n \times n$ matrices for $cost$ and $T$ , but half of the reserved space will be unused. Another option is to use a hash map.

3.3. Example

Let’s apply these algorithms to our initial example with matrices $A, B, C$ and $D$ of shapes $(4,5)$ , $(5,3)$ , $(3,10)$ , and $(10,2)$ , respectively.

First, we set the costs on the main diagonal to zero. Then, we compute the costs of $A\times B$ , $B \times C$ , and $C \times D$ .

There will be only one way to split each pair. For example:

$cost(A \times B) = cost(A) + cost(B) + 4 \cdot 3 \cdot (2 \cdot 5 - 1) = 0 +0 + 12 \cdot 9 = 108$

The same goes for $B \times C$ and $C \times D$ :

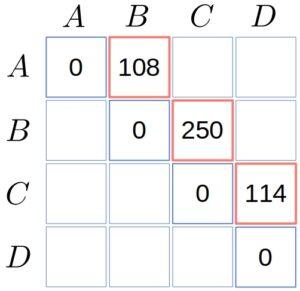
Computing the first diagonal after the base cases

We used matrix names instead of indices for readability.

Now, we focus on $A \times B \times C$ and $B \times C \times D$ :

$\begin{aligned} cost(A \times B \times C) &= \min \begin{Bmatrix} cost(A) + cost(B \times C) + 4 \cdot 10 \cdot (2 \cdot 5 - 1) = 0 +250+40\cdot 9 = 610 \\ cost(A \times B) + cost(C) + 4 \cdot 10 \cdot (2 \cdot 3 - 1) = 108 +0 + 40 \cdot 5 = 308 \end{Bmatrix} = 308 \\ cost(B \times C \times D) &= \min \begin{Bmatrix} cost(B) + cost(C \times D) + 5 \cdot 2 \cdot (2 \cdot 10 - 1) = 0 +250+10\cdot 19 = 440 \\ cost(B \times C) + cost(D) + 5 \cdot 2 \cdot (2 \cdot 3 - 1) = 114 +0 + 10 \cdot 5 = 164 \end{Bmatrix} = 164 \end{aligned}$

So:

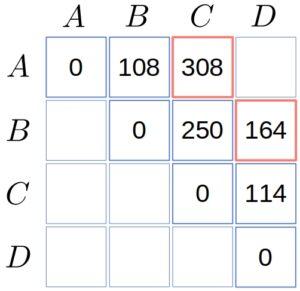
Finally, we compute $cost(A \times B \times C \times D)$ :

$cost(A, B, C, D) = \min \begin{Bmatrix} cost(A) + cost(B \times C \times D) + 72 =236\\ cost(A \times B) + cost(C \times D) + 40 = 398\\ cost(A \times B \times C) + cost(D) + 152 =460 \end{Bmatrix} = 236$

4. Reconstructing the Solution

A way to reconstruct the solution is to follow the indices in $\boldsymbol{T}$ recursively.

If $T[i, j]=k$ , where $i \leq k < j$ , that means that $A_i \times \ldots \times A_j$ should be computed as $(A_i \times \ldots A_k) \times (A_{k+1} \times \ldots \times A_j)$ . So, we need $T[i, k]$ and $T[k+1, j]$ to split $A_i \times \ldots A_k$ and $A_{k+1} \times \ldots \times A_j$ optimally:

The result of $reconstruct(T, 1, n)$ is the solution for the entire input chain $A_1 \times A_2 \times \ldots \times A_n$ .

4.1. Example

In our example, $T$ is a $4 \times 4$ matrix with the empty lower triangle:

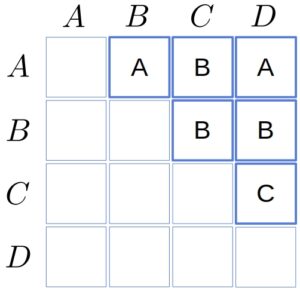
Since $T[A, D] = A$ , the first split comes after $A$ , so we have:

$A \times ( B \times C \times D)$

Since the left product is a single matrix, we focus on the right one. $T[B, D] = B$ , so we get:

$A \times \left( B \times (C \times D) \right)$

5. Memoization

Memoization is another approach. It computes $t(1, n)$ recursively following its definition. However, it avoids repeated calculations by memorizing the intermediate results:

For each pair $(i, j)$ , we first check in $memory$ if we’ve already computed $cost(i, j)$ . If so, we return $memory[i, j]$ . Otherwise, we calculate $cost(i, j)$ .

This approach is usually easier to implement than the tabular method. However, the excessive depth of the recursion tree for large $n$ can cause stack overflow.

6. Conclusion

In this article, we showed how to multiply a chain of matrices using dynamic programming.

The main difference between the tabular approach and memoization is the order in which the sub-problems are solved. The former is a bottom-up iterative approach that starts from the base cases, whereas the latter is a top-down recursive approach.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex