1. Introduction
In this tutorial, we’ll discuss secure computation and some of the practical challenges that it tries to address.
Further, we’ll discuss key cryptographic constructions that have been developed to address these challenges. In the process, we’ll understand their practical applications.
2. Challenges for Secure Computation
Cryptography has been in existence for a reasonably long period now, it even predates the advent of computers. Of course, modern cryptography kicked off with the development of computers. But, the focus was mostly on securing data in transit and data in storage.
Over the last few decades, more and more sensitive data has been generated, processed, transferred, and stored in cloud environments. Moreover, distributed and decentralized computing environments have created new challenges for cryptographic systems.
This is where secure computation plays an important role. Secure computation refers to computations where the data remains secure throughout. The emphasis here is on the security of data while in use. There are several practical applications of secure computation.
2.1. Computation on Encrypted Data
A data application typically fetches encrypted data from some form of storage on a secure network. Then, it has to decrypt the data to perform computations on them. Further, it may encrypt the outcome and send it to the storage over the secure network:
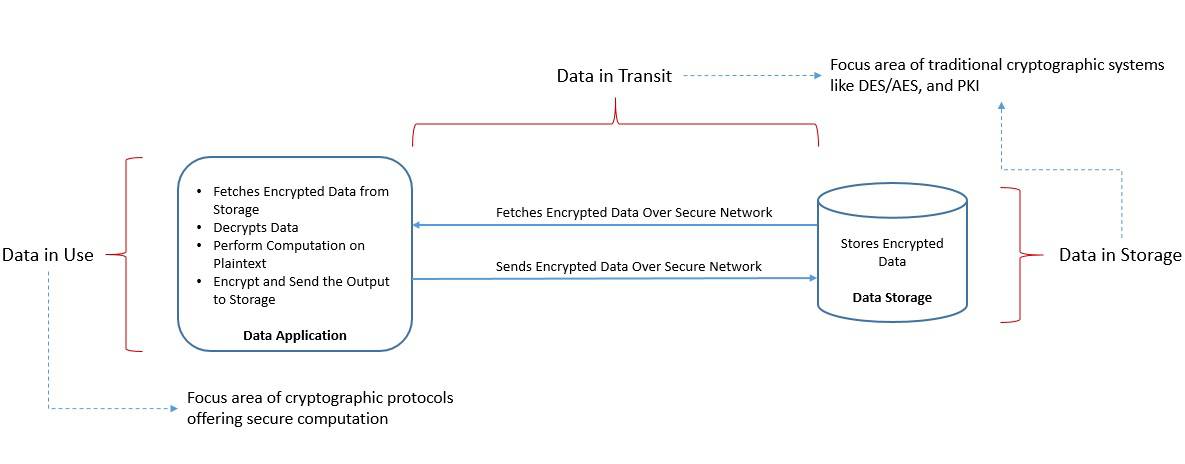
While it serves the purpose for a large part, it still leaves the data vulnerable during computation. It may not be desirable for some use cases dealing with sensitive data. What if it were possible to perform computations more securely, like without decrypting them?
2.2. Secure Distributed Computation
Distributed data computations typically involve two or more parties. Each party may be holding their data securely through encryption. In a typical scenario, one of the parties plays a central role by fetching data from others, decrypting them, and then performing the computation:
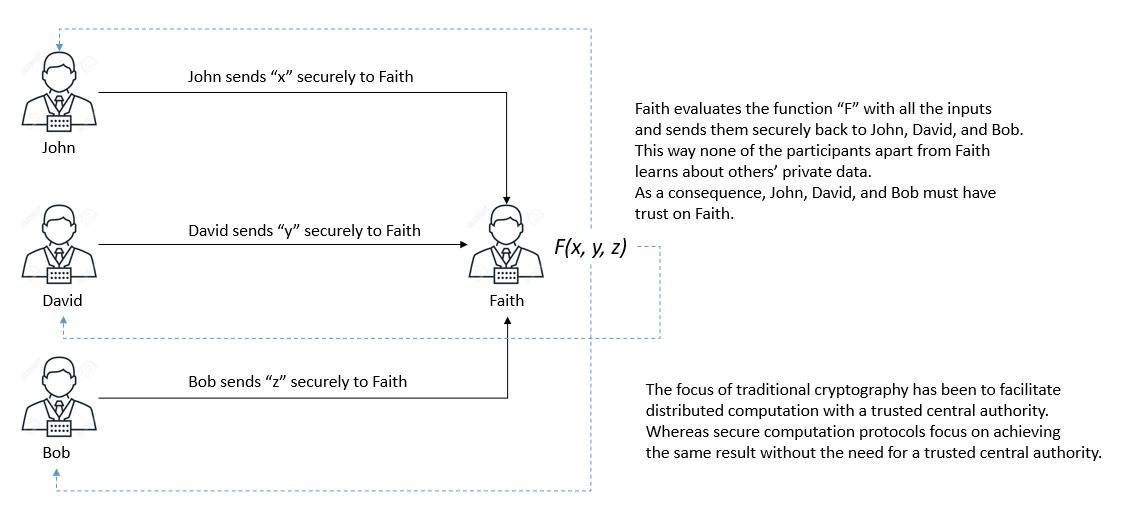
This implicitly requires trust between the central party and all other parties. However, there can be situations where each party would like to keep their data secret from the other while still participating in the computation. Is this even possible?
The challenges we’ve discussed in secure computing have been the key areas of research in cryptography for a while now. Several cryptographic constructs have been created to address some of these challenges. We’ll discuss two key cryptographic constructs in this tutorial.
3. Homomorphic Encryption
Homomorphic encryption is a type of encryption that allows us to perform computations on the encrypted data without decrypting them first. The result of such computation remains in the encrypted form:
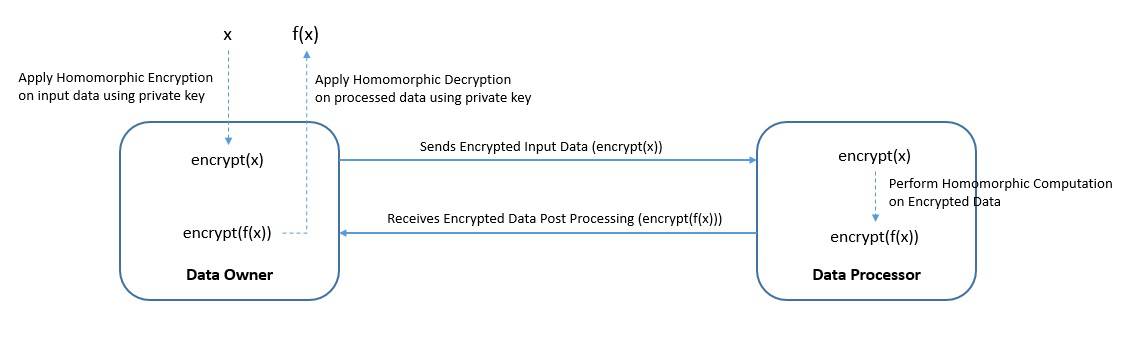
Interestingly, if we decrypt the result, it’ll be identical to the output of the exact computation had we done this on the unencrypted data in the first place.
Homomorphic encryption enables a wide range of outsourced services for sensitive data. For instance, we can send medical data to a third party for predictive analysis without worrying about data privacy concerns.
3.1. Basic Principles
The word homomorphism in algebra is a structure-preserving map between two algebraic structures of the same type. Hence, it describes the transformation of one data set into another while preserving relationships between elements in both sets:
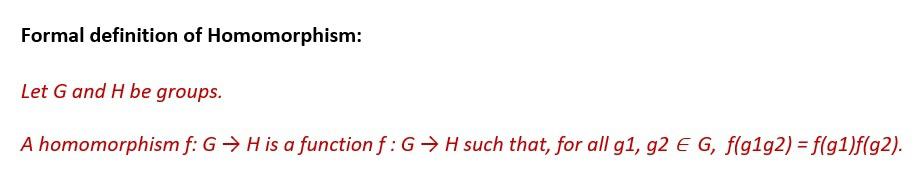
Now, extending from this definition, we can think of the encryption and decryption functions as homomorphism between plaintext and ciphertext spaces. This is the fundamental working principle behind homomorphic encryption.
In practice, homomorphic encryption works best with data represented as integers while using operations like addition and multiplication. It requires a few interactions and uses arithmetic circuits focusing on additions and multiplications.
Every operation is a mathematical function, and every function can be converted to an equivalent circuit. Hence, for every function , there is some circuit
such that
gives the same output. The circuit model of computation makes the construction of an encryption scheme simpler.
3.2. Types of Homomorphic Encryption
Homomorphic encryption includes several encryption schemes that allow us to perform different classes of computations over encrypted data:
- Partially Homomorphic Encryption (PHE): These include the schemes in which we can perform one defined operation like multiplication or addition on the ciphertext an infinite number of times. These are relatively simpler algorithms to design.
- Somewhat Homomorphic Encryption (SHE): These include the schemes which allow us to perform a limited number of operations like addition and multiplication on the ciphertext. These algorithms are relatively more difficult to design.
- Fully Homomorphic Encryption (FHE): Finally, these are the schemes where we can perform an infinite number of operations like addition and multiplication on the ciphertext. These are the most elusive homomorphic algorithms to design.
3.3. Beginning of Fully Homomorphic Encryption
Fully homomorphic encryption is often referred to as the holy grail of cryptography. It’s justifiable, considering the effort cryptographers have put into this for years. The idea of fully homomorphic encryption dates back to 1978, shortly after the RSA scheme was published.
After this, almost for three decades, researchers came up with different algorithms with partial results. For instance, the ElGamal cryptosystem (offers an unbounded number of modular multiplication), and the Goldwasser-Micali cryptosystem (offers an unbounded number of exclusive-or operations).
It wasn’t until 2009 that the first plausible construction of FHE was proposed by Craig Gentry. His idea was based on lattice-based cryptography:
It was soon followed by another construction by Marten van Dijk et al. in 2010 inspired by the earlier works of Craig Gentry, Levieil-Naccache, and Bram Cohen.
The key idea in the first-generation cryptosystems was to construct a somewhat homomorphic cryptosystem and then convert it to a fully homomorphic cryptosystem using bootstrapping. However, as more operations are performed on the ciphertext, the noise it contains keeps increasing.
3.4. The Search for Holy Grail Continues
The second-generation cryptosystems were able to provide a much slower growth of noise during homomorphic computations. These included the Brakerski-Gentry-Vaikuntanathan (BGV) scheme proposed in 2011 and the Brakerski-Fan-Vercauteren (BFV) scheme proposed in 2012, amongst others.
The third-generation cryptosystem was proposed by Craig Gentry, Amit Sahai, and Brent Waters (GSW) in 2013. The critical aspect of this scheme is that it avoids the expensive re-linearization step in homomorphic multiplication. It was later improved by FHEW in 2014 and TFHE in 2016.
Soon the fourth-generation cryptosystem was proposed by Cheon, Kim, Kim, and Song (CKKS) in 2016. It’s an approximate homomorphic cryptosystem that supports block floating point arithmetic. The search for the holy grail continues and will continue in the near future!
3.5. Implementations of the FHE
Several open-source libraries offer implementations of the key fully homomorphic encryption schemes from different generations, like BGV/BFV (second generation), FHEW/TFHE (third generation), and CKKS (fourth generation).
Shail Halevi and Victor Shoup developed the Homomorphic Encryption library (HElib) at IBM. It’s written in C++ and implements the Brakerski-Gentry-Vaikuntanathan (BGV) scheme and the Approximate Number scheme of the Cheon-Kim-Kim-Song (CKKS).
Simple Encrypted Arithmetic Library (SEAL) is another library developed by Microsoft Research. It’s also written in C++ and comes with implementing BGV/BFV schemes and the CKKS scheme. Microsoft SEAL has no required dependencies as such.
OpenFHE is an open-source project that provides implementations of the leading FHE schemes. It succeeds from earlier libraries like PALISADE (2010) and SIPHER (2014). OpenFHE was finally released in 2022 with several additional features like post-quantum public-key encryption.
3.6. Limitations of the FHE
With all the promises that fully homomorphic encryption offers, it still has very limited use. This is primarily because all fully homomorphic schemes carry a large computational overhead. This is defined by the computation time in the encrypted version vs the clear version.
Reportedly, homomorphic operations using the first version of HElib ran a trillion times slower than the corresponding plaintext operations. Of course, that has improved significantly since then, and the research to improve the performance continues.
There are other operational issues that applications employing fully homomorphic encryption tend to face. For instance, it may not be generally efficient to run very large and complex algorithms homomorphically, even when using a very efficient scheme.
Then there are complexities related to supporting multiple users in a system employing fully homomorphic encryption. The system may rely on an internal database. Now, for securing each user’s data, the system may have to support a separate database for every user.
4. Secure Multi-Party Computation
Secure multi-party computation is a subfield of cryptography that deals with methods for parties to jointly compute a function over their input while keeping those inputs private:
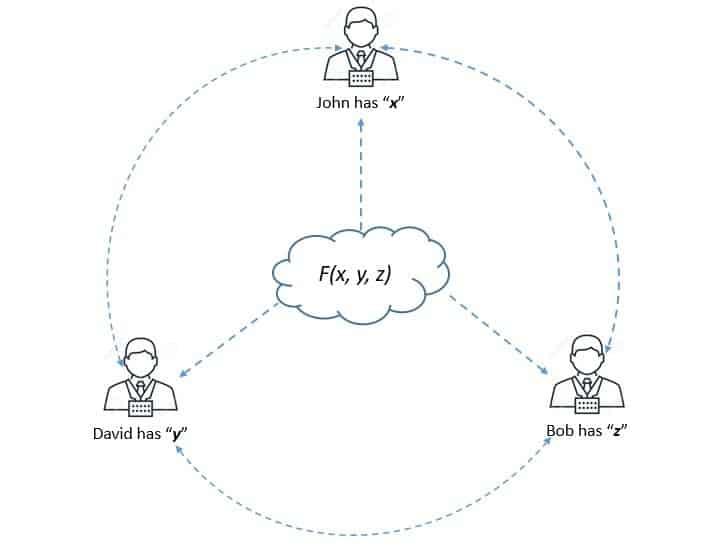
In traditional cryptography, the objective is to secure communication or storage from an outside adversary. However, the objective of secure multi-party communication is to protect participants’ privacy from each other.
Secure multi-party computation allows data scientists and analysts to compliantly, securely, and privately compute on distributed data without ever exposing it. It also has a wide range of practical applications, like electronic auctions and electronic voting.
4.1. Basic Principles
The basic formulation of a multi-party computation involves a given number of participants (,
, …,
). Each participant has their private data (
,
, …,
). The objective is to compute the value of a public function
:
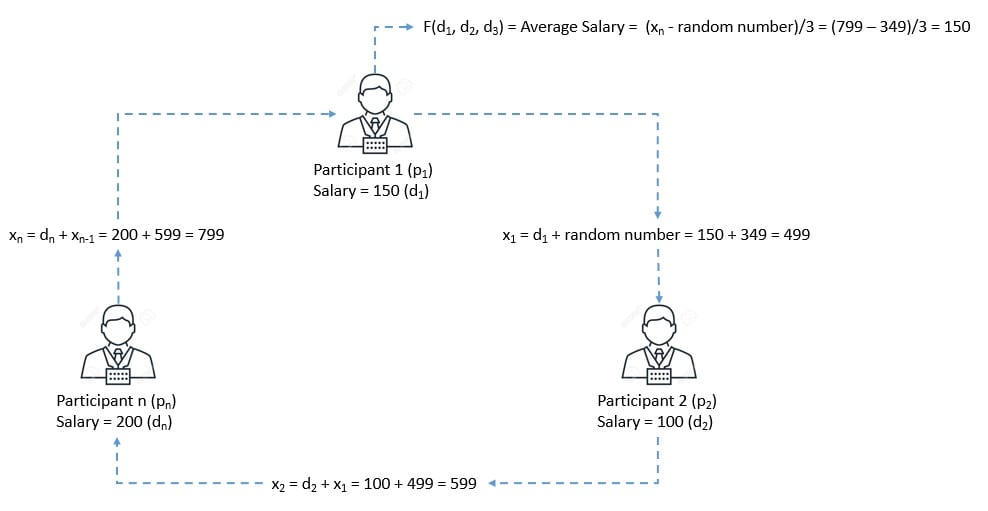
For instance, here, the objective is to compute the average salary while keeping the salary of each participant secret from other participants.
Now, a secure multi-party computation protocol should exhibit some basic properties for it to be practically useful:
- Input Privacy: This implies that no information about the private data held by the participants can be inferred from the messages sent during the execution of the protocol.
- Correctness: This implies that any subset of adversarial parties willing to deviate from the protocol should not be able to force the honest parties to output an incorrect result.
4.2. Security of Multi-Party Computation
Security is a key consideration in any multi-party computation protocol. Unlike traditional cryptographic applications, the adversary in a multi-party protocol is one of the protocol’s participants. The protocol changes significantly based on the type and number of such adversaries in a system.
Let’s assume there are participants in such a protocol where
participants can be adversarial. Now, the solutions and protocols are very different if we can assume an honest majority, defined by the condition
.
Also, we can categorize adversaries faced by such protocols based on how willing they are to deviate from the protocol. This gives rise to different forms of security:
- Semi-honest (Passive) Security: In this model, the adversaries merely cooperate to gather information from the protocol while not deviating from the protocol specification. Protocols achieving security in this model are quite efficient.
- Malicious (Active) Security: In this model, the adversaries may arbitrarily deviate from the protocol execution in an attempt to cheat. Protocols that achieve security in this model provide a very high-security guarantee, although at the cost of efficiency.
4.3. Two-party Computation Protocols
Although special purpose protocols started to appear in the 1970s, the secure computation was formally introduced as secure two-party computation in 1982 by Andrew Yao. This was specifically created to solve the famous Millionaire’s Problem.
Later, in 1986 Andrew Yao came up with the general protocol for evaluating any feasible computation. These two papers by Yao later inspired the development of what became known as Yao’s Garbled Circuit Protocol.
Yao’s protocol is secure against semi-honest adversaries and is extremely efficient regarding the number of rounds. The function here is conceived as a Boolean circuit which is a collection of gates connected with three different types of wires:
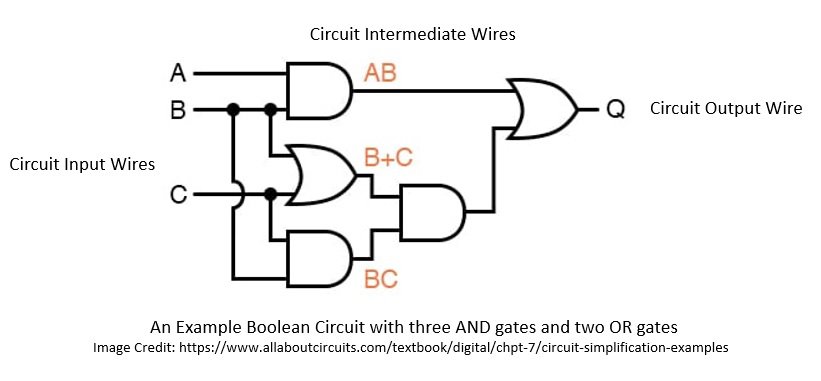
Basically, Yao’s protocol suggested how to garble a circuit so that two parties could learn the output of the circuit and nothing else. Here, the sender prepares the garbled circuit and sends it to the receiver, who obliviously evaluates the circuit:
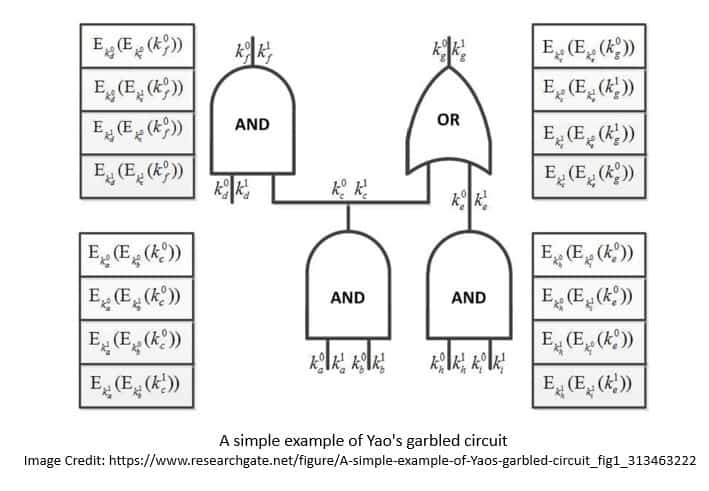
The receiver learns the encoding corresponding to both his and the sender’s output sending back the sender’s encoding. The sender completes his part of the output. He then sends the mapping from the receiver’s output encodings to bits to the receiver, allowing the receiver to obtain their output.
4.4. Multi-party Computation Protocols
The two-party computation protocols were later generalized for multi-party by Goldreich, Micali, and Wigderson (GMW). The computation here is based on the secret sharing of all the inputs and zero-knowledge proofs for a potentially malicious case.
In methods based on secret sharing, the data associated with each wire is shared amongst the parties, and a protocol is then used to evaluate each gate. the function here is defined as a circuit over a finite field, also known as the arithmetic circuit.
Two types of secret sharing are generally used; Shamir Secret Sharing, and Additive Secret Sharing. In both cases, it’s possible to distribute a secret among several parties by distributing shares to each party, where shares are random elements of a finite field:
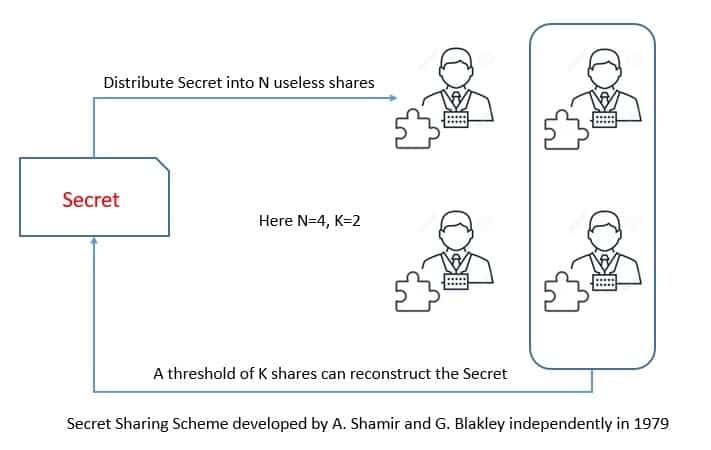
Secret sharing schemes can tolerate an adversary controlling up to parties out of
total parties. The
here varies based on the scheme and the type of adversary. For instance, the Shamir secret sharing scheme is secure against a passive adversary when
and an active adversary when
.
The additive secret sharing scheme can tolerate the adversary controlling all but one party, that is . This is while maintaining security against a passive and active adversary. SPDZ is a popular system that implements MPC with additive secret shares and is secure against active adversaries.
4.5. Implementations of the SMPC
Over the years, several practical implementations of multi-party protocols have been developed. The Fairplay system was one of the first systems offering two-party computation based on Yao’s protocol and multi-party computation based on BMR protocol.
Later many improvements came in the form of efficiency and techniques for active security. For instance, the application of the garbling technique and “cut-and-choose” paradigm for achieving active security. This was proposed by Lindell and Pinkas and later implemented by Pinkas et al. in 2009.
The more recent improvements include focusing on highly parallel implementations based on garbled circuits designed to be run on CPUs with many cores. For instance, Kreuter et al. described an implementation running on 521 cores of a powerful cluster computer.
Multiple demonstrations of the production capability of SMPC systems have been done in the recent past. For instance, Boston University prepared the Boston Women’s Workforce Council Report in 2016 where the custodian of the original data were Bostan-area employers.
However, large-scale practical applications of SMPC remain elusive. There have been many efforts in this regard lately. For instance, Security through Private Information Aggregation (SEPIA), and Secure Computation API (SCAPI) intends to provide practical implementations of SMPC protocols.
4.6. Limitations of the SMPC
As we’ve seen, SMPC protocols generally use one of the secret sharing schemes. Now, secret sharing involves communication and connectivity between all parties. This obviously leads to higher communication costs as compared to plaintext computation.
As the nature of these protocols is generally complex, they tend to have computational overhead. For instance, random numbers are generated in these protocols in order to ensure the security of the computation. This adds to the computational overhead and slows down the run time.
Lastly, as we’ve seen earlier, SMPC protocols are vulnerable to attacks from colluding parties. Now, there are always stricter protocols providing better security against such adversaries. But, these come at the cost of efficiency and impede the practical use of the protocols.
5. Application Considerations for FHE and SMPC
Secure computation is an old yet very active field of research within cryptography. We went through homomorphic encryption and secure multi-party computation in this tutorial. These technologies have matured to a level where we can use them at scale in production systems to a certain extent.
In their basic forms, these technologies address different aspects of secure computation. But they do provide very similar functionalities. In fact, there have been attempts to adapt homomorphic encryption to use multiple keys that enable multi-party computation.
There are also cases where these technologies have been combined to serve a greater purpose. For instance, there is a construction mixing multi-party computation with homomorphic encryption. Here, homomorphic encryption is used as a subroutine to produce correlated randomness.
Their application is also guided by the performance of these technologies. The performance here depends on the relative cost of computation and bandwidth. For high-bandwidth settings, multi-party computation tends to outperform homomorphic encryption.
Together these technologies are finding widespread use in industries like finance and healthcare, where data privacy has always been a concern for outsourcing data analysis jobs. Moreover, innovative and secure ways are coming up for distributed voting, private bidding, and auctions.
6. Other Secure Computation Technologies
Homomorphic encryption and multi-party computation are not the only technologies under the umbrella of secure computation. Several others serve more specific purposes. Let’s have a very quick look through some of the key technologies here:
- Functional Encryption: Functional Encryption is a generalization of public-key encryption in which processing a secret key allows one to learn a function of what the ciphertext is encrypting. Hence, it allows a party to evaluate a specific function on an encrypted input during its decryption.
- Zero-knowledge Proofs: Zero-knowledge proof is a method in which one party (the prover) can prove to another party (the verifier) that a given statement is true while the prover avoids conveying any additional information apart from the fact that the statement is indeed true.
- Differential Privacy: Differential privacy is a system for publicly sharing information about a dataset by describing the patterns of groups within the dataset while withholding information about individuals in the dataset.
- Oblivious Transfer: Oblivious transfer is a method in which a sender transfers one of the potentially many pieces of information to a receiver but remains oblivious as to what piece (if any) has been transferred.
6. Conclusion
In this tutorial, we discussed secure computation and the challenges that are present in this field of study. Further, we covered homomorphic encryption and secure multi-party computation in little detail. We went through several protocols and their implementations that are available for our use.