How to Check if a Line Segment Intersects a Rectangle?

1. Introduction

In this tutorial, we’ll show how to check if a line segment intersects a rectangle.

2. Intersection

Let’s say that the segment’s endpoints are $U(x_u, y_u)$ and $V(x_v, y_v)$ . Similarly, let $A_1(x_1, y_1)$ , $A_2(x_2, y_2)$ , $A_3(x_3, y_3)$ , and $A_4(x_4, y_4)$ be the rectangle’s corners.

We say that the segment $UV$ intersects the rectangle $A_1A_2A_3A_4$ if $UV$ has at least one common point with at least one rectangle’s side. For example:

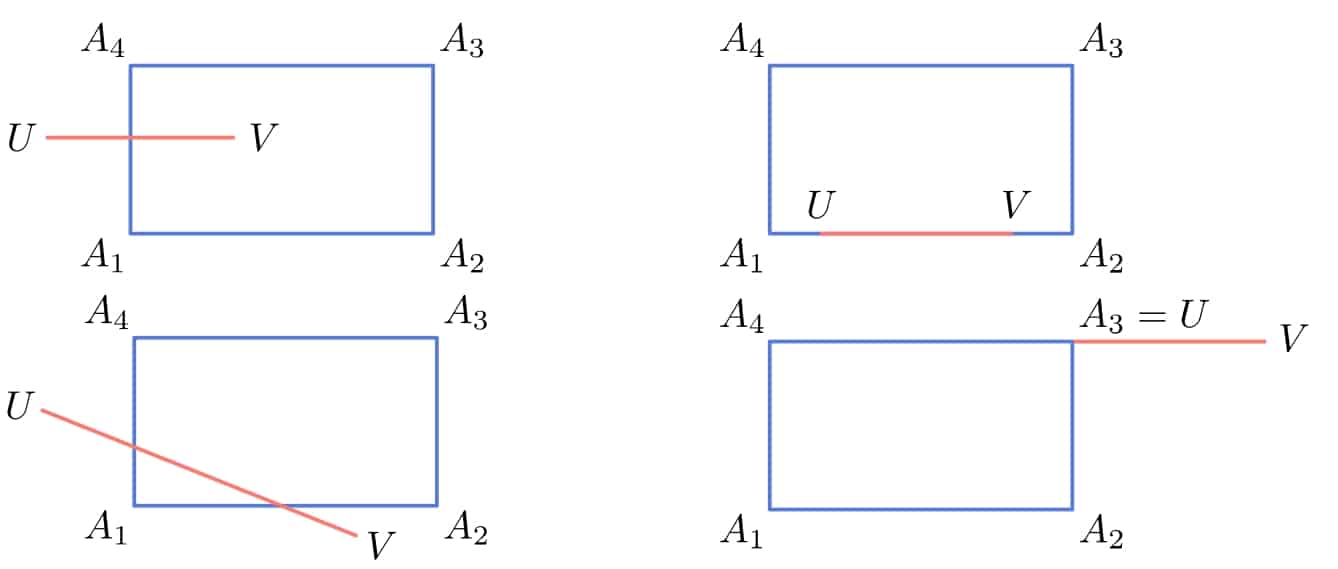
So, the idea is to check if $UV$ intersects $A_1A_2$ , $A_2A_3$ , $A_3A_4$ , or $A_4A_1$ . If we find an intersection with any side, we don’t need to check the rest.

3. The Intersection of Two Segments

So, let’s see how we can check if $UV$ intersects $A_1A_2$ . The steps will be the same for the three remaining sides.

If $UV$ intersects $A_1A_2$ , there will be at least one point $Z$ that belongs to both $UV$ and $A_1A_2$ :

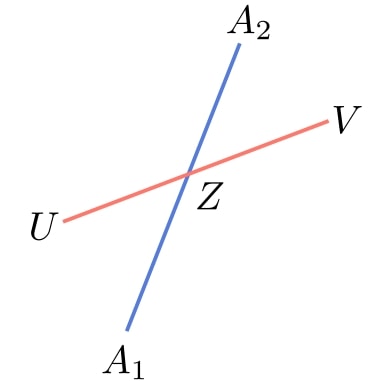
Focusing on the triangle $UA_1Z$ and treating $A_1$ , $A_2$ , $U$ , $V$ , and $Z$ as vectors directed from the origin, we see that the following must hold:

$\begin{aligned} &Z = &A_1 + \alpha(A_2 - A_1) = U + \beta(V - U) \\ &\iff &\alpha(A_2 - A_1) + \beta (U - V) = U - A_1 \\ && \alpha, \beta \in [0, 1] \end{aligned}$

The condition $\boldsymbol{\alpha, \beta \in [0, 1]}$ ensures that $\boldsymbol{Z}$ belongs to both segments.

3.1. Solving a Linear System

If $A_1=(x_1, y_1)$ , $A_2=(x_2, y_2)$ , $U=(x_u, y_u)$ , and $V=(x_v, y_v)$ , we get a system of two linear equations:

(1) $\begin{equation*} \alpha \begin{bmatrix}x_2 - x_1 \\ y_2 - y_1 \end{bmatrix} + \beta \begin{bmatrix}x_u - x_v \\ y_u - y_v \end{bmatrix} = \begin{bmatrix} x_u - x_1 \\ y_u - y_1 \end{bmatrix} \end{equation*}$

The next step is to solve it for $\alpha$ and $\beta$ .

3.2. Interpreting the Solution

If the system has no solution, $UV$ doesn’t intersect $A_1A_2$ .

If there’s a unique solution such that $\alpha \in [0, 1]$ and $\beta \in [0,1]$ , then they intersect at a single point $Z$ .

If there’s more than one solution, we’ll get a range of values for $\alpha$ and $\beta$ . If the ranges include values from $[0, 1]$ , $UV$ and $A_1A_2$ coincide at least partially. In particular, if the ranges are completely inside $[0, 1]$ , we have $UV \subseteq A_1A_2$ , $A_1A_2 \subseteq UV$ , or both.

3.2. Algorithm

Here’s our algorithm:

So, we start with one side and check all the others iteratively until we either find an intersection or test all of them without success.

Since we deal with a fixed number of dimensions, solving systems takes $O(1)$ time, so the complexity of the entire algorithm is also $\boldsymbol{O(1)}$ .

3.3. What if the Segment Is Inside the Rectangle?

We set out the problem and formulated our algorithm to test only if $UV$ has a mutual point with the rectangle’s boundary.

On the other hand, if we want to cover the rectangle’s interior, we need to extend our algorithm. The already formulated pseudocode deals with all the cases except when $UV$ lies inside the interior of $A_1A_2A_3A_4$ .

To handle it, we note that $UV$ is inside the rectangle only if $U$ and $V$ are linear combinations of the rectangle’s directed non-parallel sides such that all the coefficients are between 0 and 1:

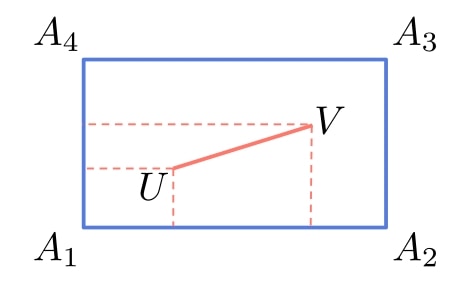
We can take any two adjacent sides as the vectors as long as we direct them so that the interior points have positive coefficients.

To check that, we solve two linear systems we derive from:

$U = \alpha_u (A_2 - A_1) + \beta_u (A_4 - A_1)$

and

$V = \alpha_v (A_2 - A_1) + \beta_v (A_4 - A_1)$

If both have single solutions $(\alpha_u, \beta_u) \in [0, 1]^2$ and $(\alpha_v, \beta_v) \in [0, 1]^2$ , $UV$ is in the interior of $A_1A_2A_3A_4$ .

4. Conclusion

In this article, we talked about how to check if a line segment intersects with a rectangle. We differentiated between two cases: in the first one, we considered if the segment intersects the rectangle’s boundary, and in the second one, the case where we covered the intersections with the interior as well.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex