Harris Corner Detection Explained

Last updated: March 18, 2024

Reviewed by: Grzegorz Piwowarek
Baeldung Pro – CS – NPI EA (cat = Baeldung on Computer Science)
announcement - icon

Learn through the super-clean Baeldung Pro experience:

>> Membership and Baeldung Pro.

No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.

1. Overview

In this tutorial, we’ll talk about Harris Corner Detection, a mathematical approach to detecting corners in an image. First, we’ll illustrate the mathematical formulation. Then, we’ll show the step-by-step procedure to perform the Harris Corner Detector.

2. Mathematical Formulation

A corner is a point whose local neighborhood is characterized by large intensity variation in all directions. Corners are important features in computer vision because they are points stable over changes of viewpoint and illumination. The so-called Harris Corner Detector was introduced by Chris Harris and Mike Stephens in 1988 in the paper “A Combined Corner and Edge Detector”.

Let’s consider a two-dimensional image I and a patch W of size m \times m centered in (x_0,y_0). We want to evaluate the intensity variation occurred if the window W is shifted by a small amount (u, v). Such variation can be estimated by computing the Sum of Squared Differences (SSD):

(1)   \begin{equation*} \hbox{SSD}(u, v)=\sum_{\left(x, y)\right \in W} g(x,y) \left[I\left(x, y\right)-I\left(x+u, y+v\right)\right]^{2} \end{equation*}

where g(x,y) is a window function that can be a rectangular or a Gaussian function. We need to maximize the function \hbox{SSD}(u, v) for corner detection. Since u and v are small, the shifted intensity I(x+u, y+v) can be approximated by the following first-order Taylor expansion:

(2)   \begin{equation*} I(x+u, y+v) \approx I(x, y)+u I_{x}(x, y)+v I_{y}(x, y) \end{equation*}

where I_x and I_y are partial derivatives of I in x and y direction, respectively. By substituting (2) in (1) we obtain:

(3)   \begin{equation*} \hbox{SSD}(u, v) \approx \sum_{\left(x, y)\right \in W} g(x, y)\left[u^{2} I_{x}^{2}+2 u v I_{x} I_{y}+v^{2} I_{y}^{2}\right] . \end{equation*}

The equation (3) can be expressed in the following matrix form:

(4)   \begin{equation*} \hbox{SSD}(u, v) \approx\left[\begin{array}{ll} u & v \end{array}\right] M\left[\begin{array}{l} u \\ v \end{array}\right] \end{equation*}

where M is a 2 \times 2 matrix computed from image derivatives:

(5)   \begin{equation*} M=\sum_{\left(x, y)\right \in W}g(x, y)\left[\begin{array}{ll} I_{x} I_{x} & I_{x} I_{y} \\ I_{x} I_{y} & I_{y} I_{y} \end{array}\right] \end{equation*}

The matrix M is called structure tensor. 

The Harris detector uses the following response function that scores the presence of a corner within the patch:

(6)   \begin{equation*} R = \operatorname{det}(M)-k \operatorname{tr}(M)^{2} . \end{equation*}

k is a constant to chose in the range [0.04, 0.06]. Since M is a symmetric matrix, \operatorname{det}(M) = \lambda_1 \lambda_2 and \operatorname{tr}(M) = \lambda_1 + \lambda_2 where \lambda_1 and \lambda_2 are the eigenvalues of M. Hence, we can express the corner response as a function of the eigenvalues of the structure tensor:

(7)   \begin{equation*} R=\lambda_{1} \lambda_{2}-k\left(\lambda_{1}+\lambda_{2}\right)^{2} . \end{equation*}

So the eigenvalues determine whether a region is an edge, a corner or flat:

  • if \lambda_1 and \lambda_2 are small, then |R| is small and the region is flat;
  • if \lambda_1>> \lambda_2 or viceversa, then R <0 and the region is an edge;
  • if \lambda_1 \approx \lambda_2 and both eigenvalues are large, then R is large and the region is a corner.

The classification of the points using the eigenvalues of the structure tensor is represented in the following figure:

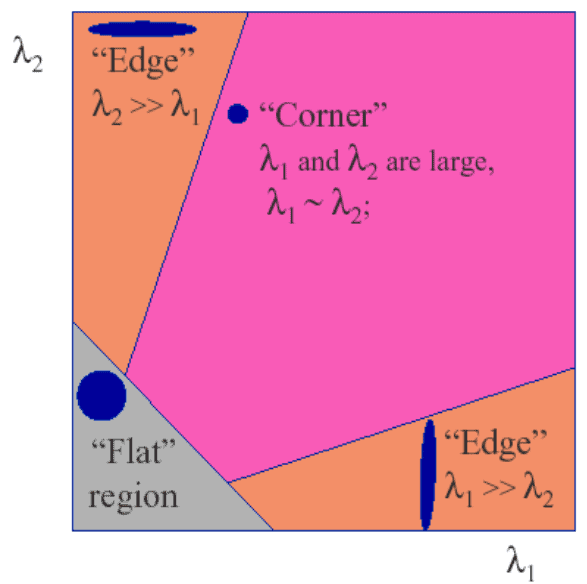
Classification of image points

 

3. Algorithm

Harris corner detector consists of the following steps.

  1. Convert the original image into a grayscale image I. The pixel values of I are computed as a weighted sum of the corresponding R, G, B values:

    (8)   \begin{equation*} I = 0.299 \cdot R+0.587 \cdot G+0.114 \cdot B \end{equation*}

  2. Compute the derivatives I_x and I_y by convolving the image I with the Sobel operator:

    (9)   \begin{equation*} I_x = \begin{bmatrix} +1 & 0 & -1 \\ +2 & 0 & -2 \\ +1 & 0 & -1 \end{bmatrix} * I \quad \mbox{and} \quad I_y = \begin{bmatrix} +1 & +2 & +1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix} * I \end{equation*}

  3. Compute the products of the derivatives I_x I_x , I_x I_y, I_y I_y.
  4. Convolve the images I_x I_x , I_x I_y, I_y I_y  with a Gaussian filter or a mean filter. Define the structure tensor for each pixel as expressed in eq. (5).
  5. Compute the response function for each pixel:

    (10)   \begin{equation*} R = \operatorname{det}(M)-k \operatorname{tr}(M)^{2} . \end{equation*}

  6. Set a threshold T on the value of R and find pixels with responses above this threshold. Finally, compute the non-max suppression in order to pick up the optimal corners.

4. Example

In the following figure we show a real application of the Harris Corner Detector. The corner response map (top-right image) was computed using Eq. 10 with k=0.04. The bottom-left image represents the thresholded corner response obtained with T=10^8. The detected corners obtained after the application of the non-max suppression are shown in the bottom-right image.

example

5. Conclusion

In this article, we reviewed the Harris Corner Detector, a fundamental technique in computer vision. We explained the mathematical formulation, and finally, we explained how to implement it.