Tournament Selection in Genetic Algorithms

1. Introduction

Genetic Algorithms (GAs) are optimization algorithms inspired by the process of natural selection. One crucial component of genetic algorithms is the selection process. The Tournament Selection is a popular selection method employed in GAs.

In this tutorial, we’ll explore the concept of Tournament Selection. First, we’ll start with a brief description of its concept. Next, we’ll examine the algorithm. Finally, we’ll look at an example to further clarify.

2. What’s Tournament Selection?

Selection is a critical phase in GAs, determining which individuals will contribute to the next generation. Individuals with higher fitness scores, indicating their suitability as potential solutions, are more likely to be selected. In fact, the goal is to simulate the survival of the fittest, favoring solutions that perform well in the given problem domain.

Tournament Selection is a popular method for choosing individuals from a population for reproduction. This is a selection operator widely used in GAs and is known for its simplicity and ease of controlling the selection pressure. Below, we’ll study the algorithm and understand why.

3. The Algorithm

Let’s now examine the Tournament Selection algorithm.

3.1. Selection Procedure

Briefly, the process involves selecting a subset of individuals from the population and then choosing the best (most fit) individual from that subset. So, we repeat this process until we’ve selected the desired number of individuals for the next generation.

Thus, we can summarize the entire procedure of the Tournament Selection into the following steps:

• Specify the tournament size (number of individuals competing in each tournament)
• Specify the total number of individuals to be selected
• Randomly choose a subset of individuals from the population, with each individual having an equal chance of being selected
• Evaluate the fitness of each individual in the subset
• Select the individual with the highest fitness score as a parent
• Repeat the process until the required number of individuals has been selected

3.2. Pseudocode

Let’s first examine the algorithm for a tournament. The algorithm below describes the procedure for selecting an individual in a tournament. There are two inputs to the algorithm: a list of individuals that have been randomly selected from a population and the size of the list.

/* Select the fittest individual (or chromosome) from a randomly selected list of individuals T */
algorithm Tournament(T, k):
    // INPUT
    //   T = a list of individuals randomly selected from a population.
    //   k = the tournament size. In other words, the number of elements in T.
    // OUTPUT
    //   the fittest individual.
    Best <- T[1];
    for i from 2 to k do
        Next <- T[i];
        if Fitness(Next) > Fitness(Best) then
            Best <- Next;
    return Best;

According to the algorithm above, we initially need to select the first individual in the list as the best one (the most fit).

Then, we need to compare the fitness of the currently selected individual with the fitness of the next one in the list. If the next individual in the list has the highest fitness score, then we just select it as the new best individual. Afterward, we should repeat this step until we compare all individuals in the list.

When we finished, the individual selected will be the one with the highest fitness score in the list. In other words, the fittest individual won the tournament.

However, when we’re using this method as a GA operator, we don’t want to choose just one individual. Instead, we want to select a subset of the population for reproduction.

In this sense, the algorithm below presents the complete procedure for the Tournament Selection. For this algorithm, instead of a randomly pre-selected list of individuals, the input is the entire population. Also, there are two other inputs: the tournament size and the total number of individuals we wish to select.

/* Assume we wish to select n individuals from the population P */
algorithm TournamentSelection(P, k, n):
    // INPUT
    //   P = the population.
    //   k = the tournament size, such that 1 ≤ k ≤ the number of individuals in P.
    //   n = the total number of individuals we wish to select.
    // OUTPUT
    //   the pool of individuals selected in the tournaments.
    T <- an empty sequence;
    B <- an empty sequence;
    for i from 1 to n do
        Pick k individuals from P at random, with or without replacement, and add them to T;
        B[i] <- Tournament(T, k);
        T <- [ ]
    return B;

Following the algorithm above, first of all, we need to create two empty lists. The first list (T) will be intended to store individuals who will compete in the tournaments. The second one, B, will be used to store the individuals who will be selected in the tournaments (the “winners”).

At this point, we then have to choose a subset of individuals from the population at random. Next, we call the Tournament algorithm (presented earlier), giving as input the randomly selected individuals as a list and the tournament size. When we receive the winning individual from the tournament, we add it to the list of the fittest individuals (B).

So, after we run the tournament and add the returned individual to the list of the fittest ones, we clear the list for the next round. Then, we repeat the process until we’ve the required number of individuals in B, according to the parameter. Thus, we can use the obtained individuals as parents for reproduction in the GA.

4. An Example

Now that we’ve seen the whole procedure, let’s take a look at an example. In this example, we’ll focus on finding the fittest individual from a list of individuals selected at random.

The figure below illustrates a tournament selection with a population of 13 individuals. Here, the individuals are represented by their respective chromosomes. And, for simplicity, each chromosome is represented by just one letter:

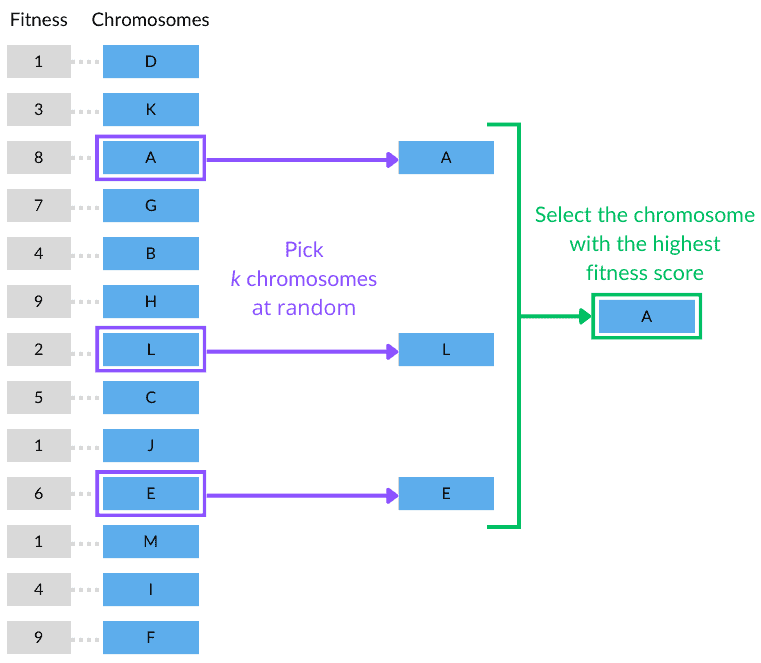
In this case, the tournament size is set to 3, i.e., . Thus, we randomly picked chromosomes A, L, and E from the population. Soon, we then compared the fitness of the three chromosomes and selected A, which had the highest score.

After that, to select the complete set of individuals who will be the parents of the next generation, we just need to run this tournament more times.

5. Analysis

Now, let’s analyze the complexity of the algorithm and the effects of its parameters.

5.1. Complexity Analysis

In each tournament, we need to compare the fitness scores of all individuals. However, to obtain the total number of individuals, we run tournaments. Therefore, the complexity of the Tournament Selection algorithm is .

5.2. The Effects of Tournament Size

As well as directly influencing the execution time of the algorithm, the tournament size also has other important effects. So, the larger the tournament size, the greater the chance that B (the list of winners) will contain members of above-average fitness.

Thus, as increases, the probability of selecting a high-fitness member increases, and of selecting a low-fitness member decreases. Specifically, this means that we can control the selection pressure by varying . Consequently, the higher the value of , the higher the selection pressure.

6. Conclusion

In this article, we studied the Tournament Selection algorithm. As we’ve learned, Tournament selection is one of the most used selection operators in GAs due to its simplicity and easy pressure control.

To summarize, the algorithm consists of randomly selecting a group of individuals from the population and selecting the most fit. Then, we just repeat this process until we have the total number of individuals who will be the parents of the next generation.