Recognizable vs. Co-recognizable vs. Decidable Languages

1. Introduction

In this tutorial, we’ll study recognizable, co-recognizable, and decidable languages.

Most problems we deal with in computing are decision problems. For example, determining if a string is a palindrome is a decision problem because there’s a binary output for every word (yes or no).

Such problems have a direct correspondence to languages. A language $\boldsymbol{L}$ represents a problem $\boldsymbol{P}$ if and only if we can map any instance of $\boldsymbol{P}$ to a word $\boldsymbol{w \in L}$ and vice versa. This allows us to study those problems using the results of the theory of formal languages and Turing machines.

However, we don’t solve those problems using Turing machines. Instead, we formulate algorithms and use higher-level programming languages to implement them. This isn’t an issue for computer science theory since we can convert those algorithms to Turing machines.

2. Turing Machines and Languages

First, let’s revise how a Turing machine (TM) works.

A TM accepts a word if it ends in an accepting state after reading the entire word. The language a machine $\boldsymbol{M}$ recognizes consists of all the words it accepts – $L(M)$ . Analogously, a TM rejects a word if it finishes in a non-accepting state after reading it.

However, a TM can end in a loop for some input words. In that case, we say it neither accepts nor rejects the input.

3. Language Categorization

For each language $L$ , we can ask if a Turing machine $M$ accepts all the words from $L$ . We can ask about its complement $\overline{L}$ .

Based on the answers, we categorize languages into three types:

3.1. Recognizable Languages

A language $\boldsymbol{L}$ is recognizable if there’s a Turing machine $\boldsymbol{M}$ that accepts all the words $\boldsymbol{w \in L}$ . Nothing is implied about the complement of $L$ . The machine can reject a word from $\overline{L}$ or run forever in a loop.

For example, let $L = \{a^k b^{\ell} c^m \mid k = 1,2,\ldots \land {\ell} = 1,3,5,\ldots \land m = 2,4,6,\ldots \}$ .

For any string $w \in L$ , a recognizer of $L$ should switch between its states based on the counts of $a$ , $b$ , and $c$ in $w$ . If it finds at least one $a$ , an odd number of $b$ s, and an even number of $c$ s, it will accept an input word. So, $L$ is recognizable.

3.2. Co-recognizable Languages

A language $L$ is co-recognizable if its complement $\overline {L}$ is recognizable.

Therefore, a Turing machine must exist for $\overline{L}$ . That means an algorithm (a TM) can accept a word that isn’t in the language $L$ but rejects or run forever if the input is in $L$ .

For instance, the language of Turing machines that don’t halt on empty input is co-recognizable. Here, our input is a string representation of a TM. We run it on the universal Turing machine, and if it halts, we identify a machine from the complement language. Since we can’t end the simulation to return a yes if the machine halts when we feed it an empty input, we can’t recognize the target language.

So, a language can be co-recognizable but not recognizable, and vice versa. It can also be neither. However, some languages are both.

3.3. Decidable Languages

A language $\boldsymbol{L}$ is decidable if it’s recognizable and co-recognizable:

$(\exists M_L, M_{\overline{L}}) L=L(M_L) \land \overline{L}=L(M_{\overline{L}})$

A decider is a TM that always halts. We can construct a decider for $L$ by combining $M_{L}$ and $M_{\overline{L}}$ :

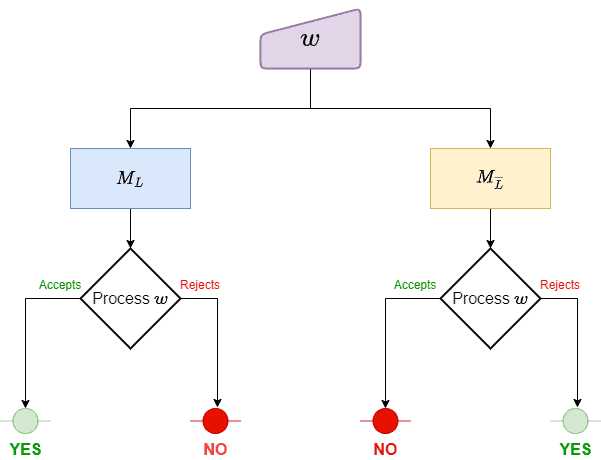
It forwards the input $w$ to both $M_{L}$ and $M_{\overline{L}}$ . Now, by construction, if $w \in L$ , then $M_{L}$ will accept it and $M_{\overline{L}}$ won’t. The converse holds for $w \in \overline{L}$ . So, we define the decider’s output based on which constituent machine accepts or rejects the input word. Since $L$ is recognizable and co-recognizable, one of them is guaranteed to accept it.

So, a decider always halts, but a recognizer can end in a loop if the input word belongs to the complement of the language it recognizes.

4. Conclusion

In this article, we’ve gone through language categorization based on the Turing machine. A language is decidable if it’s both recognizable and co-recognizable.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex