How to Check If a String Is a Palindrome? | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll learn how to check if a string is a palindrome.

2. What’s a Palindrome?

A palindrome is a string symmetric around the middle. For example:

$abcde\boldsymbol{f}edcba$

The first and last characters are the same, just as the second and the second-to-last, the third and the third-to-last, etc.

That yields a recursive definition. A string $x=x_1 x_2 \ldots x_{n-1} x_n$ is a palindrome ( $palindrome(x) = true$ ) if $x_1 = x_n$ and $x_2 \ldots x_{n - 1}$ is also a palindrome. The base cases are an empty string and a string of length one: we consider them palindromes. So, the recursive definition is:

$palindrome(x_1 x_2 \ldots x_{n-1} x_n) = \begin{cases} true,& n \in \{0, 1\} \\ x_1 = x_n \land palindrome(x_2 \ldots x_{n-1}), & n > 1 \end{cases}$

2.1. Odd and Even Lengths

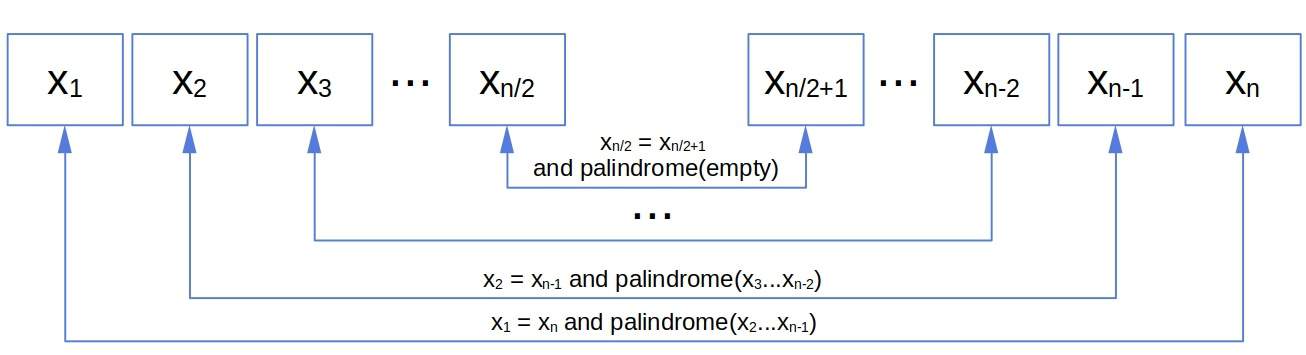
Does it cover the cases with even and odd string lengths? If $n$ is even, and $x$ is a palindrome, the recursive steps meet right between the middle elements $x_{n/2}$ and $x_{n/2+1}$ . Those constitute the last pair to check. Afterward, the next to handle is the empty string, whose length is 0 and is by definition a palindrome:

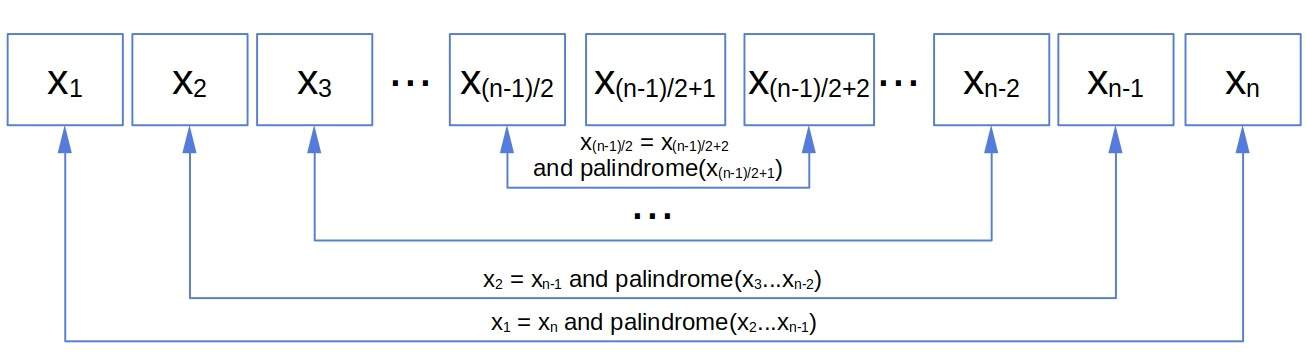
Similarly, if $n$ is odd, the last pair are $x_{(n-1)/2}$ and $x_{(n-1)/2+2}$ , the immediate predecessor and successor to the middle element $x_{(n-1)/2+1}$ . A string of length 1 is a palindrome, so the definition covers this case too:

3. 3. Recursive Algorithm to Check if a String Is a Palindrome

We’ll base the recursive algorithm on our definition:

First, we check for the base case. Then, if the current endpoints are the same, we continue checking the rest of the string. Otherwise, we return $false$ since we found a pair of characters that isn’t in line with the definition.

3.1. Complexity

In the worst case, the string is a palindrome, so all the pairs have to be checked. Since there are $\boldsymbol{\lfloor n/2 \rfloor}$ pairs, the time complexity is $\boldsymbol{O(n)}$ .

However, if $\boldsymbol{n}$ is very large, there’s a possibility to get a stack overflow error. It happens when the recursion is so deep that it exhausts the entire call stack. We can address this issue by converting our recursive algorithm into an iterative one.

4. Iterative Algorithm

If we rewrite the recursive algorithm’s innermost if-statement as $return (x_1 = x_n) \land palindrome(x_2 \ldots x_{n-1})$ , we’ll get a tail recursion. We can convert it into an iterative algorithm:

In the iterative algorithm, we run the while-loop until hitting the base case or finding a pair that breaks the palindrome property. In each iteration, we check if the current endpoints ( $x_{left}$ and $x_{right}$ ) are the same. If so, we move $left$ one character to the right and $right$ one character to the left, applying the same check to the new endpoints. Otherwise, if $x_{left} \neq x_{right}$ , we exit the loop and return $false$ .

The iterative algorithm works the same as the recursive one but isn’t prone to stack overflow.

5. Conclusion

In this article, we presented recursive and iterative algorithms for checking if a string is a palindrome. The former follows the recursive definition of a palindrome but may cause a stack overflow if the input string is too long.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex