From Recursion to Iteration – Factorial Function Example

1. Overview

Recursion and iteration are the basic ways to execute a given set of instructions in programming languages repeatedly. Although recursion has its advantages, iterative algorithms are often preferred for their efficiency and space optimization.

In this tutorial, we’ll explore how to convert a recursive factorial function into an iterative one using the tail recursive method.

2. Recursion and Iteration

Recursion and iteration are two methods for repeatedly executing a set of instructions:

Recursion: it’s when a function calls itself inside its code, thus repeatedly executing the instructions present inside it
Iteration: it’s when a loop runs a set of instructions multiple times until a specific condition is met like in “for” and “while” loops

3. Converting Simple Recursive Functions

The simplest case to handle is tail recursion. Thus, the method recommended is to convert all recursive calls into tail calls.

3.1. Converting Recursive Calls to Tail-Recursive

Let’s take a look at how to make simple recursive calls into tail calls:

Let’s find a recursive call that’s not a tail call
Then we need to understand what is going on between that recursion call and its return statement
Let’s now extend the function with a new accumulator argument. Then, we choose the default value of the accumulator as a value that causes it to do nothing to the main function
To make the recursive call into a tail call, we need to eliminate the extended feature between the call and its return statement. In each step, we’ll verify that the function is equivalent to its original
Let’s repeat all the steps until all recursive calls are tail calls

3.2. Converting Tail-Recursive to Iterative Functions

Let’s now take a look at the steps to convert a tail-recursive function into an iterative function:

Study the function
Convert all recursive calls into tail calls
Introduce a one-shot loop around the function body
Convert tail calls into “continue” statements
Tidy up

4. Example: Factorial Function

With such a simple function, we could skip straight to the iterative version without utilizing any strategies. But the goal here is to create a mechanical process that we can rely on when our functions aren’t so straightforward. So, we’ll work on the factorial function to concentrate on the process.

4.1. The Recursive Factorial Algorithm

The factorial function is a common example used to demonstrate recursion. Here’s an example of the factorial function using a recursive algorithm:

algorithm Factorial(n):
    // INPUT
    //    n = a natural number
    // OUTPUT
    //    n! = the factorial of n

    if n < 2:
        return 1
    else:
        return n * Factorial(n - 1)

4.2. Converting to a Tail Call

In this step, we’ll convert the recursive call to a tail call. In short, we have only one problematic line ${ \textbf{return } {n } \times Factorial(n-1)}$ , which we have to extend using an accumulator:

First, we take the original function and add an additional argument “acc”, which is the accumulator that plays the role of the multiplier. Then, we’ll set ${acc = 1}$ as a default value, which has no effect until we give it some other value
Second, we change every single return statement from ${\textbf{return }{(whatever)}}$ to ${\textbf{return } acc \times {(whatever)} }$ :

algorithm Factorial(n, acc = 1):
    // INPUT
    //    n = a non-negative integer
    //    acc = the accumulator to hold the intermediate factorial results (default is 1)
    // OUTPUT
    //    n! = the factorial of n

    if n < 2:
        return acc * 1
    else:
        return acc * n * Factorial(n - 1)

As a result, it computes the factorial of ${n-1}$ and then multiplies it by ${acc \times n}$ . However, we don’t need to do the multiplication ourselves. Using the accumulator argument, we can now ask our extended factorial function to do it for us. The algorithm below presents the tail call after substituting the extended factorial function with ${ \textbf{return } Factorial(n - 1, acc \times n)}$ :

algorithm Factorial(n, acc = 1):
    // INPUT
    //    n = a non-negative integer
    //    acc = the accumulator, initially set to 1
    // OUTPUT
    //    n! = the factorial of n

    if n < 2:
        return 1 * acc
    else:
        return Factorial(n - 1, n * acc)

4.3. Converting to a Factorial Iterative Function

After converting the recursive call to a tail call, we can convert it to an iterative function by introducing a one-shot loop around the function body ${\textbf{While } \text{(True)}}$ { $Body; Break;$ } :

algorithm Factorial(n, acc = 1):
    // INPUT
    //    n = a natural number
    //    acc = the accumulator, default is 1
    // OUTPUT
    //    n! = the factorial of n

    while true:
        if n < 2:
            return 1 * acc
        else:
            return Factorial(n - 1, n * acc)
        break  // Let's follow the steps for now and we'll tidy the code later

4.4. Replacing Recursive Tail Calls

Let’s now replace all the recursive tail calls ${\textbf{function(x=x1, y=y1, ...)}}$ with ${\textbf{(x, y, ...) = (x1, y1, ...); continue;}}$ :

algorithm Factorial(n, acc = 1):
    // INPUT
    //    n = a natural number
    //    acc = the accumulator, default value is 1
    // OUTPUT
    //    n! = the factorial of n

    while true:
        if n < 2:
            return 1 * acc
        else:
            (n, acc) = (n - 1, acc * n)
            continue

        break

4.5. Cleaning up the Code

Let’s clean up the code and make it more appropriate:

algorithm Factorial(n, acc = 1):
    // INPUT
    //    n = a natural number
    //    acc = the accumulator to store the intermediate results, default is 1
    // OUTPUT
    //    n! = the factorial of n

    while n > 1:
        (n, acc) <- (n - 1, acc * n)

    return acc

4.6. What Have We Accomplished?

Here’s the build-up of stack frames using different methods to compute the factorial of 3:

Let’s discover the stack frames using factorial with recursion:

Here’s the build-up of stack frames using factorial with a tail call:

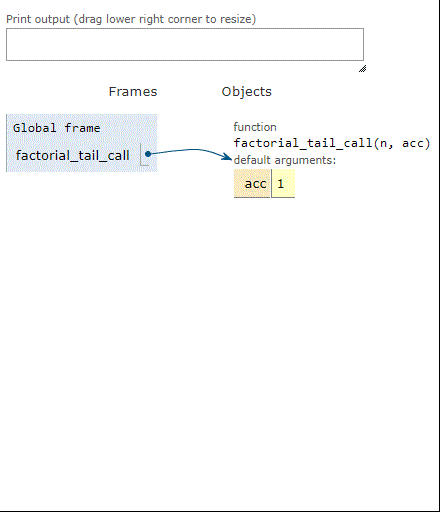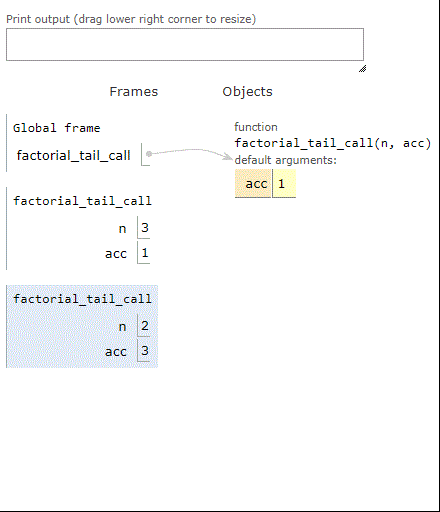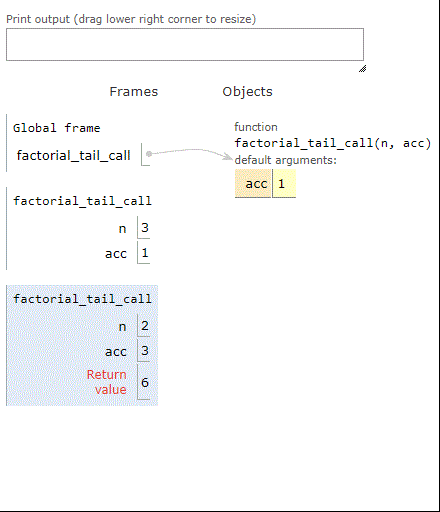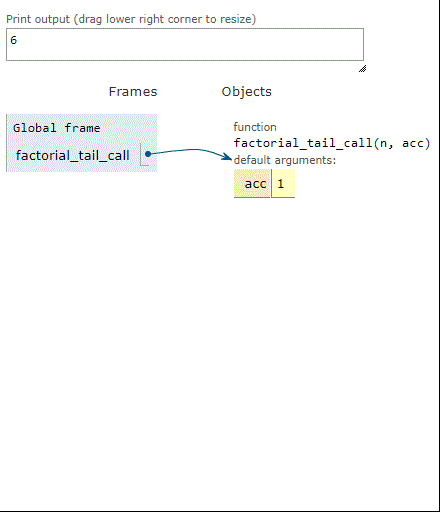
Here are the stack frames using factorial with iteration:

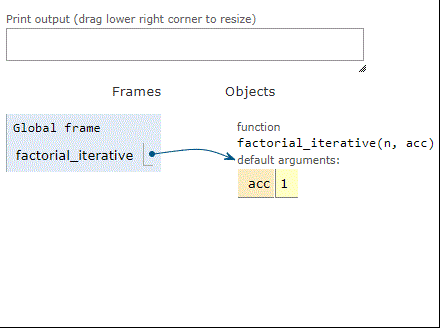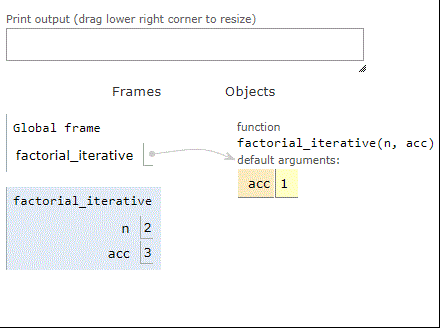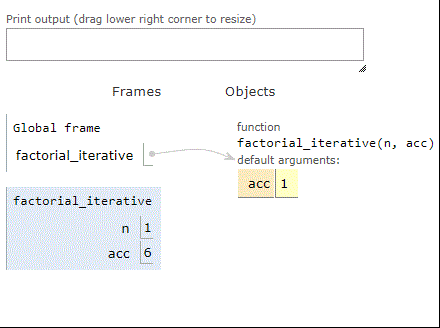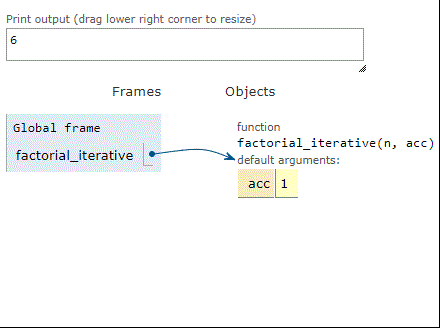
As we can see, when factorial is computing the factorial of 3, three frames build up on the stack. Same thing for the tail-recursive factorial. However, the iterative factorial uses just one stack frame, over and over, until it’s done. In short, we converted ${O(n)}$ stack use into ${O(1)}$ stack use.

5. Converting Complex Recursive Function

Here are some methods to convert a complex recursive function to a tail-recursive function:

Trampoline method: the idea behind the trampoline is to remove the current execution frame from the stack manually, eliminating stack build-up before making a tail call. This method is the stepping stone to a more-general technique named the continuation-passing style
The Continuation-Passing Style (CPS) method: this technique is more-general, in which functions do not return values; rather, they pass control onto a continuation, which specifies what happens next

After converting the recursive function to a tail recursive, we can follow the steps in section $\mathbf{4.1}$ to make the iterative form of our function.

6. Conclusion

In this tutorial, we explored the difference between the recursive and iterative approaches. We also discussed converting a simple recursion into an iterative function using the tail-recursive approach. Then, we applied this strategy to the factorial function. We can use this method to optimize the performance of various recursive functions.

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex

Full Archive

About Baeldung