Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll talk about three basic terms in deep learning that are epoch, batch, and mini-batch. First, we’ll talk about gradient descent which is the basic concept that introduces these three terms. Then, we’ll properly define the terms illustrating their differences along with a detailed example.
To introduce our three terms, we should first talk a bit about the gradient descent algorithm, which is the main training algorithm in every deep learning model.
Generally, gradient descent is an iterative optimization algorithm for finding the minimum of an objective function. In the case of deep learning, the objective function corresponds to the loss function of the network.
The gradient descent algorithm works in two steps that are performed continuously for a specific number of iterations:
In the image below, we can see how gradient descent works in the case of one-dimensional variables:
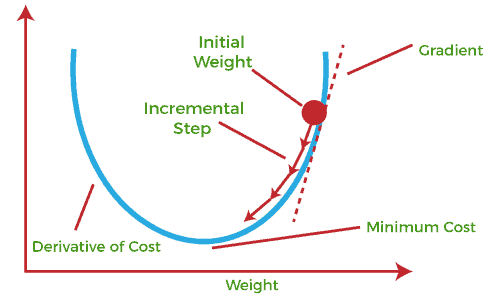
In the case of a neural network, we pass the training data through the hidden layers of the network to compute the value of the loss function and compute the gradients of the loss function with respect to the parameters of the network. Then, we update the parameters accordingly.
There are three types of the gradient descent algorithm based on the amount of training data that are used to perform one iteration of the algorithm.
In batch gradient descent, we use all our training data in a single iteration of the algorithm.
So, we first pass all the training data through the network and compute the gradient of the loss function for each sample. Then, we take the average of the gradients and update the parameters using the computed average.
In the diagram below, we can see how batch gradient descent works:
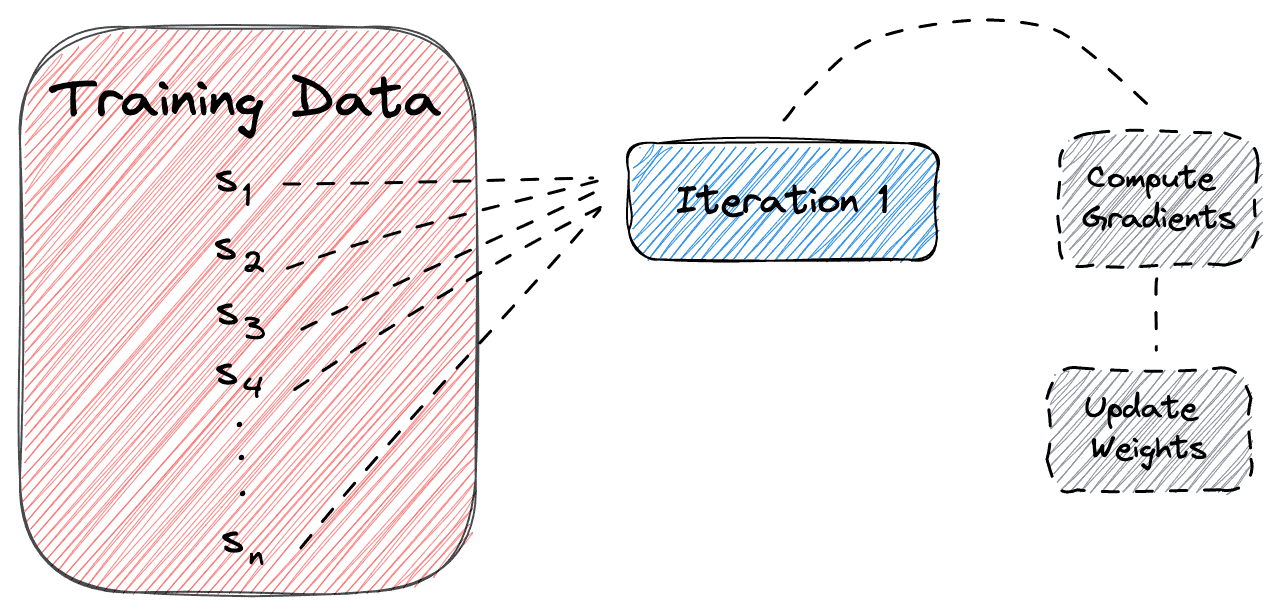
The previous method can be very time-consuming and inefficient in case the size of the training dataset is large. To deal with this, we use stochastic gradient descent, where we use just one sample in a single iteration of the algorithm.
In the diagram below, we can see how stochastic gradient descent works:
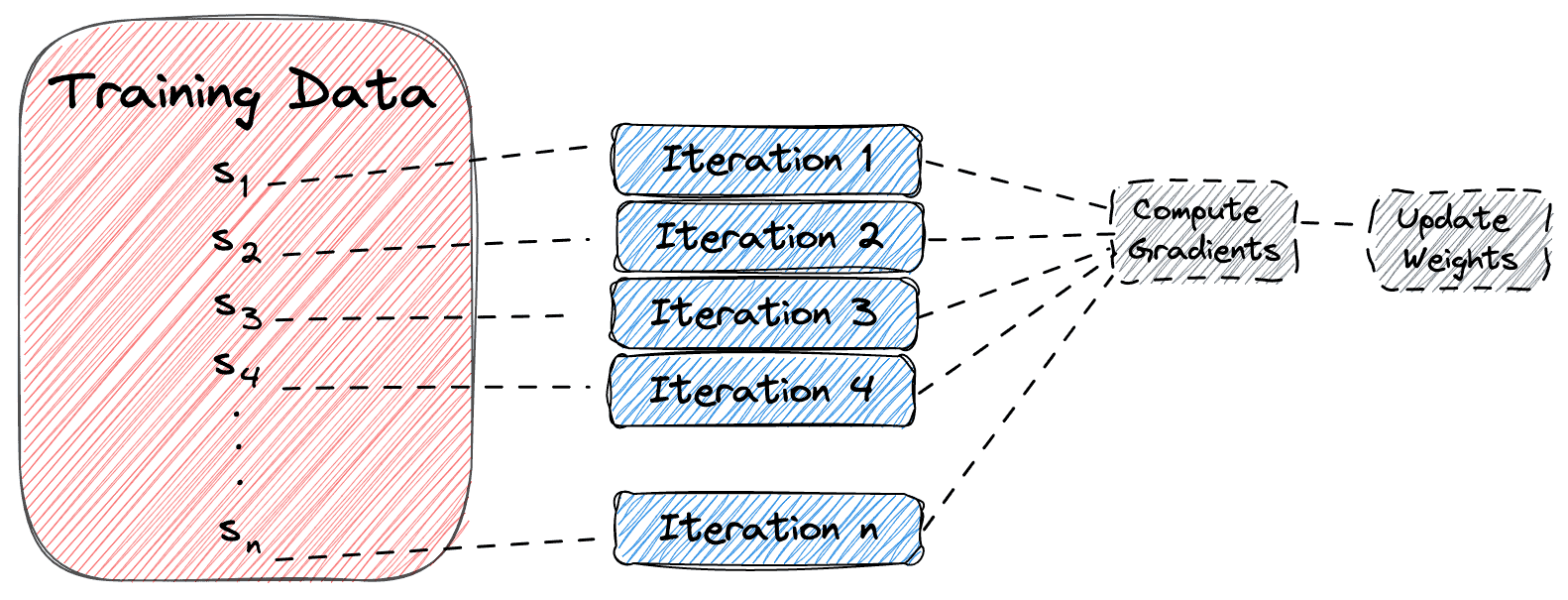
A drawback of the stochastic gradient descent is the fact that by using just one sample, the loss function is not necessarily decreasing in each iteration. In the long run, the method will never reach the global minimum since there will be a lot of fluctuations in the value of the loss function.
Mini-batch gradient descent is a combination of the previous methods where we use a group of samples called mini-batch in a single iteration of the training algorithm. The mini-batch is a fixed number of training examples that is less than the actual dataset. So, in each iteration, we train the network on a different group of samples until all samples of the dataset are used.
In the diagram below, we can see how mini-batch gradient descent works when the mini-batch size is equal to two:
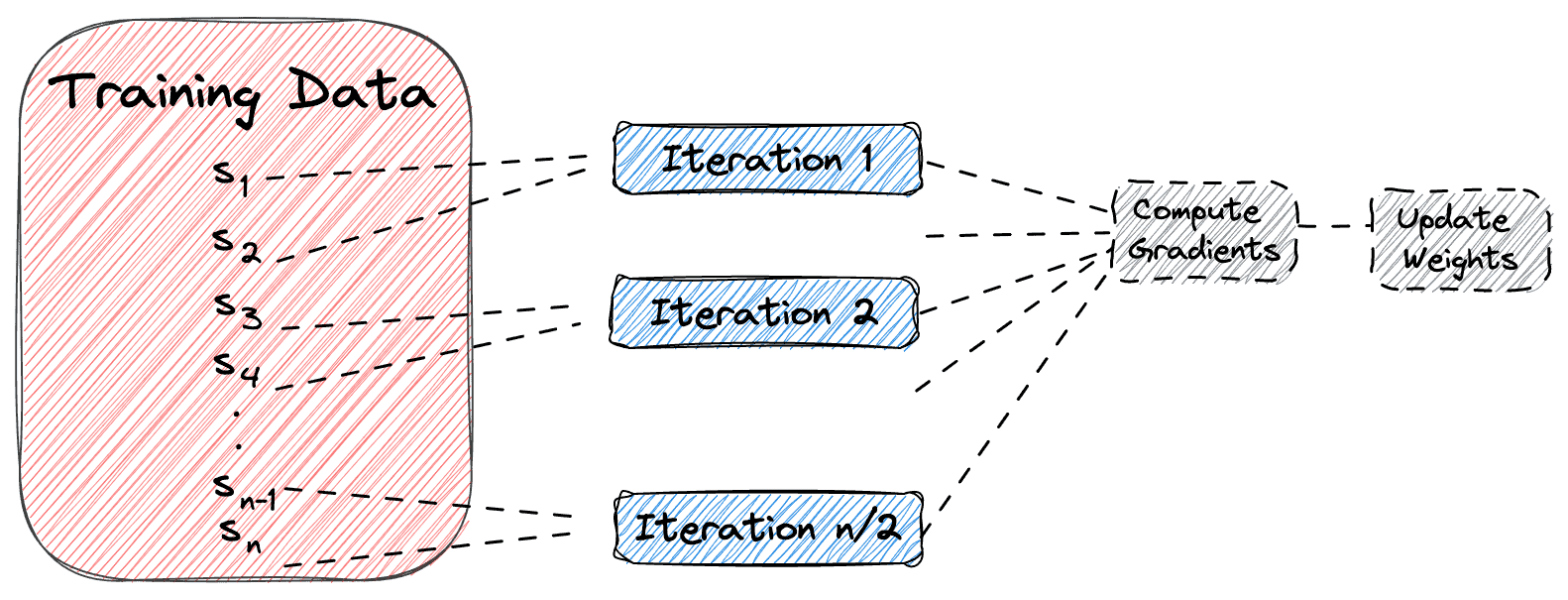
Now that we have presented the three types of the gradient descent algorithm, we can move on to the main part of this tutorial.
An epoch means that we have passed each sample of the training set one time through the network to update the parameters. Generally, the number of epochs is a hyperparameter that defines the number of times that gradient descent will pass the entire dataset.
If we look at the previous methods, we can see that:
We have already defined the other two terms but let’s re-introduce them more formally.
So, a batch is equal to the total training data used in batch gradient descent to update the network’s parameters. On the other hand, a mini-batch is a subset of the training data used in each iteration of the training algorithm in mini-batch gradient descent.
Finally, let’s present a simple example to better understand the three terms.
Let’s assume that we have a dataset with samples, and we want to train a deep learning model using gradient descent for
epochs and mini-batch size
:
In this tutorial, we talked about the differences between an epoch, a batch, and a mini-batch. First, we presented the gradient descent algorithm that is closely connected to these three terms. Then, we defined the terms and presented a simple example.