Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: October 8, 2023
In this tutorial, we’re going to look at some of what it takes to encode the details needed for a game of chess.
The first thing that we need to understand is what we’re actually encoding. Chess is a relatively simple game on the surface, but with a lot of nuance to it.
The first thing we need to be able to do is represent the position of every piece on the board. Chess consists of a board of 64 squares in an 8×8 grid, with up to 16 pieces on each side, of 6 different types. If the need is to encode the current state of the board simply, then this is all we need to store.
However, some of the additional rules require us to track some more information. For example:
If we need to encode the current state of the game, then we need to incorporate all of those into our stored data as well.
Let’s start with just encoding the current state of the board. This means we’ll be ignoring the extra rules and concentrating on getting the correct position of all the pieces.
There are two different ways we can approach this – board-centric or piece-centric.
A board-centric approach means that we’re storing one value for each square on the board. This means exactly 64 pieces of information. Each of these values is then the piece that is in that square. To represent this, we need to track:
However, we also have an additional option – the square is empty. This gives us 13 different combinations for each square, which we can store as a 4-bit number. This will then allow us to store the entire board as 256 bits, or 32 bytes of data.
We can do better, though. For example, let’s try applying run-length encoding to our data. This means that we store both the appropriate value and the number of times it’s repeated instead of storing each repetition.
The maximum possible number of repetitions on a chess board is 64 – when every square has the same value. This means that we can store the repetitions in 6 bits and still need 4 bits to identify the contents, meaning that each value is now 10 bits long.
Our most compressible setup with all the pieces on the board is when all identical pieces are adjacent. In this case, we have 13 different values, each being repeated an appropriate number of times, meaning that we can store the board in 130 bits or 17 bytes. (Our most compressible setup is actually where every square is identical, which is 64 repetitions of the same square and will need only 10 bits to represent.)
A more realistic setup is the starting layout. In this, all of the pawns are adjacent, and all of the empty squares are adjacent, but nothing else is:
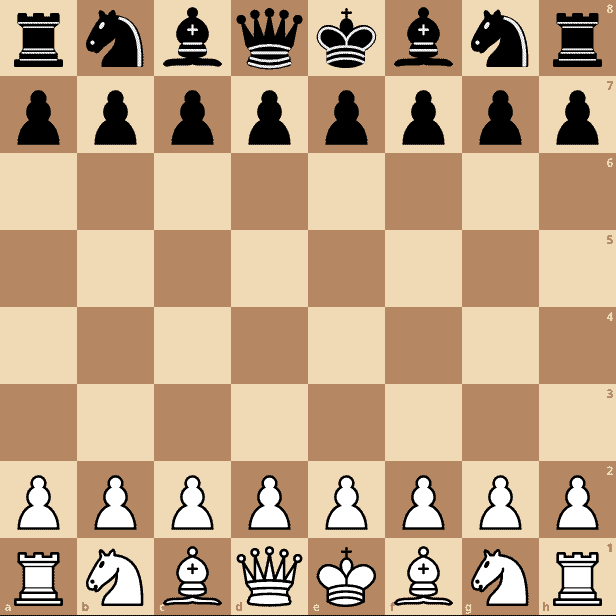
This then needs us to encode 19 different values, meaning we can store the board in 190 bits or 24 bytes. This is 75% of our previous requirement.
However, the worst case is when nothing is adjacent. This is highly unlikely to ever really happen but is technically possible. In this case, we now need to encode 64 different values, meaning that we now need 640 bits, or 80 bytes, to store the entire board. This is 250% of our previous requirement.
What if we used a shorter encoding for our length? For example, let’s try only storing the length in 4 bits instead. This means that we can only represent 16 repetitions in a single value, but most of the time, we need less than that anyway.
For our starting layout, we now need 20 values instead of 19 – we need to represent the 32 blank squares as two blocks of 16. However, we’re storing 8 bits for each and not 10. That means that we can store the entire board in 160 bits, or 20 bytes, instead of 190 bits. For our worst case, we now need 512 bits instead of 640 bits, which saves 20%. This is still worse than no run-length encoding at all but better than our previous attempt.
We can then graph the space needed for these two board layouts for each possible encoding length. Remember that no run-length encoding means we need 256 bits to store the board. Anything less than that is an improvement:
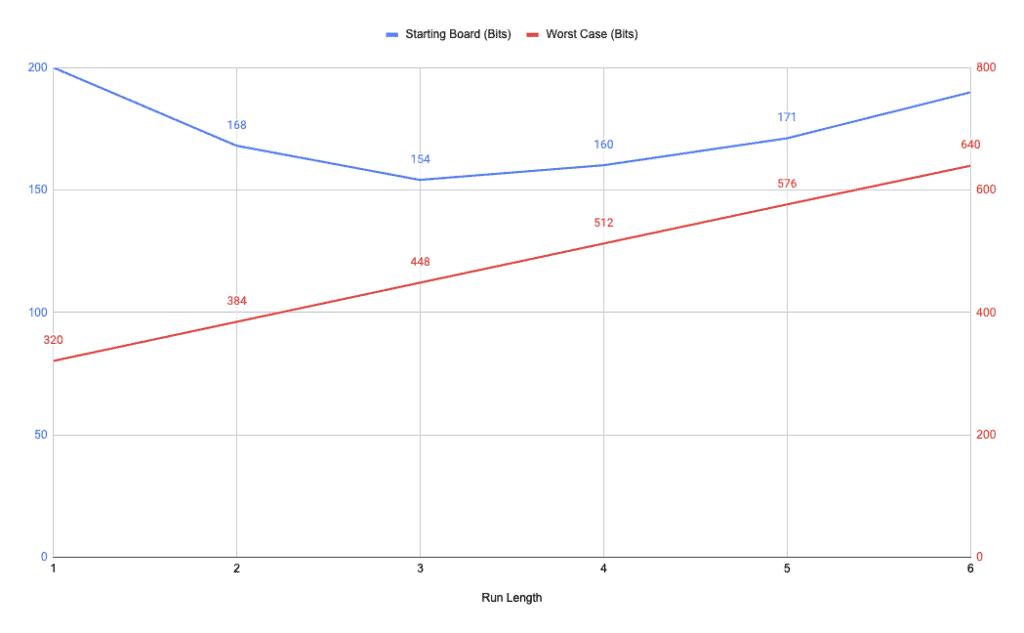
Here we can see that using 3 bits for the encoding length gives us the best space efficiency for the starting layout and is roughly in the middle for the worst-case layout.
What if instead of encoding what pieces are on each square, we encoded what squares each piece was on? Doing this will mean that we need to encode fewer values – the maximum number of pieces on the board is 32.
As an initial attempt, we’ll encode each value to represent which piece and then which square it is. As before, we need 4 bits to represent the piece itself. We then need 6 bits to represent which of the 64 squares the piece is on. This means that we need 10 bits per piece, which is 320 bits, or 40 bytes, for the maximum number of pieces. (We need to include which piece each value represents because of promotion rules, which means we don’t know how many of each piece there is.)
Surprisingly, this is worse than we saw earlier, even though we encode fewer values. This is simply because we need to store more data about each value.
What if we added some compression here as well? We know we can have up to 8 of any given piece. That means that we can store each value as:
(If we factor in promotions then it’s technically possible to have 10 of the same piece, but supporting this actually results in worse storage for little benefit.)
In this case, we need to store details about 12 types of pieces, with between 1 and 8 locations for each. This gives us a total of 276 bits or 35 bytes. This is still worse than our board-centric encoding.
Where this encoding really benefits is when there are fewer pieces on the board. Let’s imagine a late-game scenario:
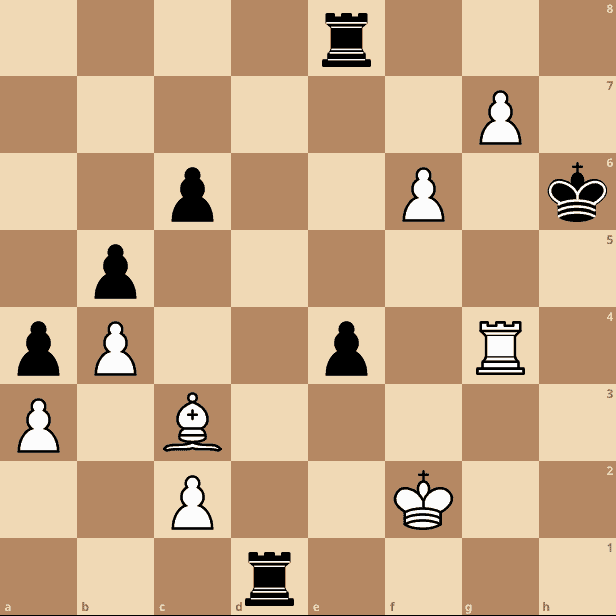
In this case, our board-centric encoding must encode 30 different runs of values, taking 7 bits each. This means it’ll need 210 bits or 27 bytes to store this.
Conversely, our piece-centric encoding will need to encode 15 different pieces of 7 different types. This will need 139 bits, or 18 bytes, to store. This is a saving of 34% to represent the exact same board layout.
What we’ve seen here is good enough for encoding the current state of any given board. However, it’s not quite good enough to represent the state of the game that got us here. There are a number of extra pieces of information that we need to achieve this.
Firstly, we need to know whose turn it is. We can represent this as a single bit of data since there are only two possible values.
Next, we need to know if castling is still possible. The rules for this are that castling is possible if the king and rook involved have never moved and if there are no pieces between them. We already know if there are any pieces between them based on the board layout, but we need to track if those pieces have ever moved. We can do this by storing a single bit for each rook – initially set to 1 and cleared if the rook or king moves. That means storing an additional 4 bits.
En Passant is a rule that allows a pawn to capture an opposing pawn that has just made an initial 2-square advance and is now on an adjacent square. However, we can only do this the turn after the other player made the 2-square advance. This means that we need to know which pawns are allowed to perform this move.
The obvious way is to store a piece of data for each pawn indicating this. However, we can do better than that. Because each player only moves one piece per turn, and because en passant is only allowed after a pawn has made a 2-square advance, we can store the pawn that has just done this advance. This means storing one of 17 values – 16 different pawns that could have just moved, and an extra value for when none have. This means we can represent this in 5 bits.
However, we can improve on this further. We only need to consider the pawns from the side that has just moved, reducing it down to 8 instead of 16. Further, we only need to consider the pawns that are in the appropriate rank. This means that there’s a maximum of 7 possible pawns to consider – the 8th rank must be the pawn doing the capturing. If we then treat any illegal value – i.e. a value greater than the number of possible pawns – then we can represent this in 3 bits instead.
Finally, we need to consider stalemate. There are three ways this can happen, but we’re only interested in two of them:
Some moves mean that all past states are no longer representable. For example, pawns can only ever move forward and can never be replaced, so if a pawn ever moves or is captured, then all previous states are impossible to recreate. However, this still leaves many possible moves that each need to store the entire game state.
What we’ve seen so far, ignoring the threefold repetition rule, allows us to store the game state in 14 bits plus whatever it takes to represent the board state. However, this rule changes things by forcing us to store the board state for every move. If we use the uncompressed board-centric encoding as a basis here, that’s an additional 256 bits of data for every move.
What if, instead, we stored the list of played moves?
We’ll start off doing this by recording the starting and ending squares of each move. We don’t need to know anything more than this – the piece being moved is identified by the square they’re coming from. This means that we need 12 bits per move. On average, a chess game lasts for 40 moves each, which will take 960 bits to encode.
However, we can do better than this. Chess algebraic notation is a shorthand notation for exactly this purpose and includes some shortcuts we can take advantage of. If the move is unambiguous, then we can record only the target square, and when it is ambiguous, we have simpler ways to disambiguate it.
Specifically, any move can be encoded as the target square, and then either nothing more, indicating which piece was moved – needing 4 bits – or the starting square – needing 6 bits. We also need an indication of exactly what we’re recording, which needs another 2 bits. This means we can record each move as either 8, 12 or 14 bits.
We can arguably do better by ignoring the rule for the moved piece. This means we store the target square and optionally the starting square, and then only need 1 bit to know what we’re storing. This can be done in either 7 or 13 bits. However, it’s much more common that the piece moved disambiguates the move than the square it moved from, For those cases, we’re now storing 13 bits instead of 12.
This seems like more data, but only when we actually need it.
If we use this to encode the moves for the first game between Kasparov and Deep Blue in 1996 then we’ll need 1,124 bits to encode all 50 moves made by each player. This seems much larger than our other methods, but remember that this lets us answer the threefold repetition rule as well, which would have otherwise taken 12,800 bits just for that rule.
Encoding in this way is essentially event sourcing. Rather than storing the current state, we’re storing all of the events that led up to that state. From these, we can recreate the entire game at any point, including enough to check our threefold repetition rule that was giving us trouble before.
We’ve seen here a few different techniques that can be used to encode the state of a chessboard, depending on exactly what the needs are. This includes directly representing the board all the way to an event-sourcing solution for storing all of the moves. Why not try implementing some of these yourself?