Disjoint Set Union Data Structure | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll cover the Disjoint Set Union (DSU) data structure, which is also called the Union-Find data structure. Initially, we have a universe $U$ of $n$ elements: $U = \{a_1, a_2, ..., a_n\}$ , and we’re interested in separating elements into independent (non-intersecting) sets. Additionally, we must support the union operation of two sets. Lastly, for any given element, we must be able to find the set it belongs to.

2. DSU Operations Overview

Usually, the applications that use DSU are interested in two types of queries:

Check query: do two elements $a$ and $b$ belong to the same set
Union query: unite the sets containing the elements $a$ and $b$ . Of course, if the elements belong to the same set, nothing is done

To support such queries, DSU defines the following operations:

$MAKE-SET(a)$ – create a set which contains the single element $a$
$FIND-SET(a)$ – find the set which contains the element $a$
$UNION(a, b)$ – unite the sets which contain the elements $a$ and $b$

Let’s understand how the two types of queries can be answered by supporting the defined operations. $MAKE-SET(a)$ is called initially for each element of the universe to put in its own set. When we’re trying to decide if two elements are in the same set for the check query, we perform $FIND-SET(a)$ and $FIND-SET(b)$ , and if the returned values match, then they’re in the same set. The union query is covered by simply performing the $UNION(a, b)$ operation.

3. DSU Representation

The efficiency of operations supported by DSU depends on the structure we select for representing the sets. There are several representations, but the most efficient is the forest of trees. In the representation, each independent set is a rooted tree, and all the trees together form the forest. In each set, we designate the representative of the set, which can generally be any element of the set. Still, in the forest representation, the representative of the set is the root element of the tree.

Additionally, a tree node contains a set element and a link to the parent node. The parent of the root node is the root itself. Following this idea, the representative of a set can be found by following the parent links up the tree, starting from any node until we get to the root node.

Let’s walk over the process of forest construction. Assume we have a universe $U = \{a, b, c, d, e, f\}$ that will be used to construct DSU as a forest of trees. Originally, we put each element in its own independent set, thus, initially, we get six trees in the forest by performing six operations $MAKE-SET(x), x \in \{a, b, c, d, e, f\}$ :

Now, any $FIND-SET(x)$ returns $x, x \in \{a, b, c, d, e, f\}$ . Let’s unite some of the sets. First, let’s perform $UNION(b, e)$ and $UNION(c, d)$ . The resulting forest is:

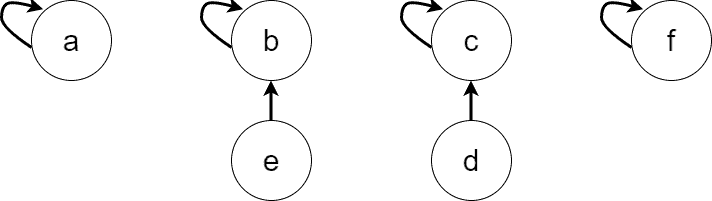
four trees, two single node trees, a and f, and two double node trees, b and c

Now, $b$ and $e$ belong to the same set, and $b$ is the representative of that set, so $FIND-SET(e) = FIND-SET(b)= b$ . Similarly, $FIND-SET(d) = FIND-SET(c) = c$ . Second, let’s perform $UNION(a, f)$ , and then $UNION(a, b)$ . We get the forest:

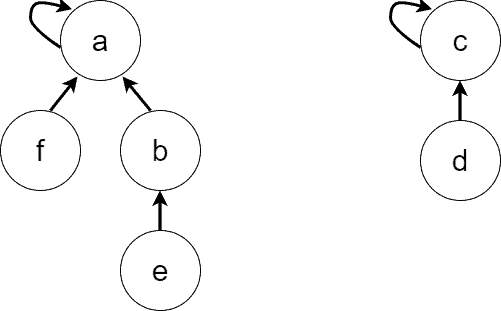
tree a with four nodes, and tree c with two nodes

4. Pseudocode for the Naive Versions of the Operations

The Naive versions of the operations implement the ideas discussed so far. $MAKE-SET(a)$ simply creates a tree with a single node for the element $a$ , and the parent link of the node points to itself. For clarity, we’d need an auxiliary operation $CREATE-NODE(a)$ , which creates the initial node of a tree:

The pseudocode for $MAKE-SET(a)$ is as simple as:

$FIND-SET(a)$ returns the node with the representative element of the set to which the element $a$ belongs. To achieve that, we start from the node containing the element $a$ and follow the parent links until we find a node $R$ for which $R = R.parent$ :

$UNION(a, b)$ appends the root of the $b's$ tree to the root of the $a's$ tree:

5. The Complexity of the Operations

$MAKE-SET(a)$ is a constant operation as it creates a tree node and puts the set element $a$ into the created root node.

$FIND-SET(a)$ is a linear operation. Indeed, its complexity depends on the height of the tree to which $a$ belongs, and we can come up with a sequence of $UNION(a, b)$ operations which build a long linear tree. Thus, the naive $FIND-SET(a)$ is an $O(n)$ operation, where $n$ is the size of the universe $U$ .

$UNION(a, b)$ is also an $O(n)$ operation as it relies on $FIND-SET(a)$ to perform its duty, and besides that it performs $O(1)$ work by reassigning the parent link of the $b's$ tree.

6. Optimization Strategies

As we see, the bottleneck operation holding DSU back from being a constant time data structure is $FIND-SET(a)$ . Thus, let’s see what optimizations we can perform to make the operation faster.

6.1. Path Compression Heuristics

The first idea is to shorten the tree height during the $FIND-SET(a)$ operation. To do that, we change the parents of all the nodes on the path from $a's$ node to the root node. How? We make all the parents point directly to the root node. The action has the effect of converting a deep tree into a flat tree. Let’s see an example:

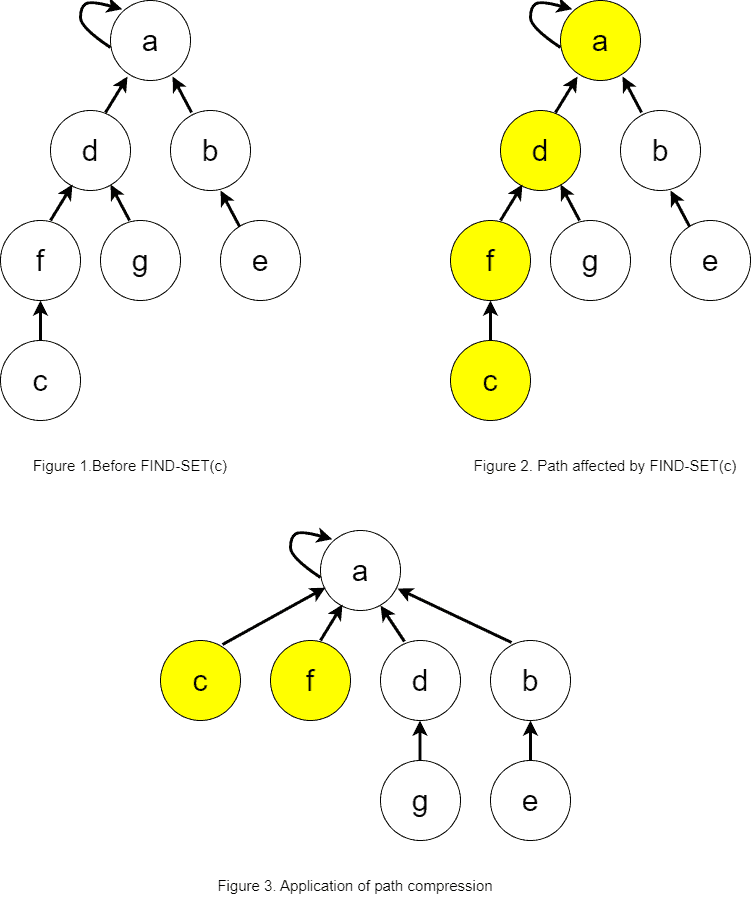
An example showing how to flatten a tree so that more nodes point directly to the root node of the tree.

In ‘Figure 1’, we can see the tree prior to performing $FIND-SET(c)$ operation. ‘Figure 2’ marks the path affected by $FIND-SET(c)$ . Finally, ‘Figure 3’ shows the effect of the path compression heuristics and the marked nodes are the ones which paths have been shortened.

The pseudocode of $FIND-SET(a)$ takes the form:

Of course, we could implement $FIND-SET(a)$ iteratively, but the recursive version is shorter and more readable.

6.2. Union by Rank Heuristics

The second optimization occurs during the $UNION(a, b)$ operation. While in the naive implementation of $UNION(a, b)$ we simply hang the $b's$ tree on the root of the $a's$ tree, now we’ll be more selective and won’t allow tree heights to grow fast.

To have a criterion for deciding how to unite two trees, we define the notion of the tree rank. We may define the rank of a tree to be the size of the tree (the number of nodes), though some references define the rank to be the upper bound of the tree’s height. Regardless of the rank selection approach, we hang the tree with the smaller rank to the root of the tree with the bigger rank. When the ranks are equal, we can select the tree to be hung arbitrarily. Also, let’s pay attention to the fact that path compression doesn’t change tree ranks regardless of the rank selection approach.

For our discussion, let’s choose the tree-size approach for the rank. The example below demonstrates the union by rank heuristics:

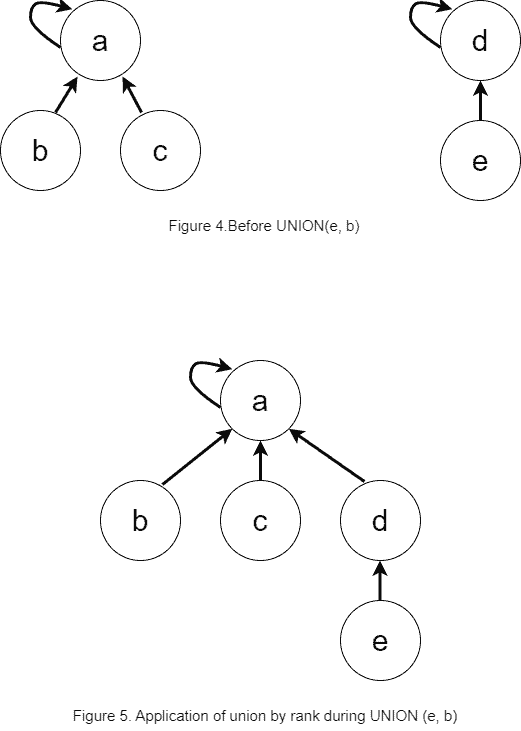
An example showing how to hang nodes on the tree to keep it as flat as possible.

The rank of the left tree in ‘Figure 4’ is three, while the rank of the right tree is two. Thus, we hang the right tree on the root of the left tree. We can see the result of the operation in ‘Figure 5’.

The pseudocode of $UNION(a, b)$ with union by rank takes the form:

Though the union by rank heuristics is performed in the $UNION(a, b)$ operation, it speeds up $FIND-SET(a)$ . $UNION(a, b)$ is optimized indirectly as it depends on $FIND-SET(a)$ .

7. The Complexity of the Operations with the Optimizations

The modified operations with the optimizations applied are estimated using the amortized analysis. We’ll only provide the results of optimizations without digging into the details of complexity analysis as it’s vast and complex.

It turns out that each optimization separately speeds up the operations. But when the two optimizations are applied together, they make the DSU operations run in $O(\alpha(n))$ time, where $\alpha(n)$ is the inverse Ackermann function. $\alpha(n)$ is a very slowly growing function and for any possible practical value of $n$ , $\alpha(n) \leq 4$ . Thus, practically all the DSU operations run in constant time on average.

A detailed analysis of the complexity can be found in chapter 21.4 of the book “Introduction to Algorithms, third edition” by Thomas H. Cormen et al.

8. Application in Graph Problems

There are some practical applications of DSU in graph problems. Let’s denote an undirected graph by $G$ , the graph vertices by $G.V$ , and the graph edges by $G.E$ . We’ll assume the graph has $N$ vertices and $M$ edges.

8.1. Finding the Connected Components of an Undirected Graph

The problem of finding the connected components appear in various applications. For example, imagine a black-and-white picture where we want to count the number of black regions. The pixels of the image can be treated as vertices of the graph, and two adjacent pixels are connected with the edge if they have the same color. We can solve the problem using DSU.

The algorithm of finding the connected components is simple: initialize DSU with $MAKE-SET(v), v \in G.V$ . Then, iterate over the edges of the graph and unite the sets of the two vertices of each edge. In the end, each set represents a connected component:

Additionally, we might need to perform a linear scan over the vertices of the graph to see which connected component each vertex belongs to. The algorithm complexity is $O(N + M)$ .

The problem of finding the connected components can also be solved using DFS or BFS algorithms which have the same complexity (though they are easier to implement). DSU wins over DFS or BFS for solving the problem when there’s an additional condition to preserve the connected components’ information while adding new edges to the graph.

8.2. Usage of DSU in Kruskal’s Algorithm

Another popular usage of DSU is in the Kruskal’s algorithm for finding the minimum spanning tree of an undirected graph. The straightforward implementation of Kruskal’s algorithm runs in $O(Mlog(M) + N^2)$ time. DSU improves the asymptotic to be $O(Mlog(M) + M) = O(Mlog(M))$ .

In Kruskal’s algorithm, we first sort the edges by their weights in increasing order. Then, we iterate over the sorted edges in increasing order of weights, and we unite the sets of each edge’s vertices if they are in different sets (connected components). In a connected undirected graph, there can be a maximum of $N - 1$ union operations, after which we get the minimum spanning tree:

9. Conclusion

In this article, we introduced the DSU data structure, defined its operations, and described the best representation of DSU as a forest of trees. Then we demonstrated ways to optimize the operations to create a near-constant time data structure. Additionally, we showed some of the applications of DSU in graph problems.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex