Topological Sort of Directed Acyclic Graph

1. Introduction

In computer science, a directed acyclic graph (DAG) is a directed graph with no cycles. In this tutorial, we’ll show how to make a topological sort on a DAG in linear time.

2. Topological Sort

In many applications, we use directed acyclic graphs to indicate precedences among events. For example, in a scheduling problem, there is a set of tasks and a set of constraints specifying the order of these tasks. We can construct a DAG to represent tasks. The directed edges of the DAG represent the order of the tasks.

Let’s consider a problem with how a person might get dressed for a formal occasion. We need to put on several garments, such as socks, pants, shoes, etc. Some garments must be put on before the others. For example, we need to wear socks before shoes. Some garments can be put on in any order, e.g., socks and pants. We can use a DAG to illustrate this problem:

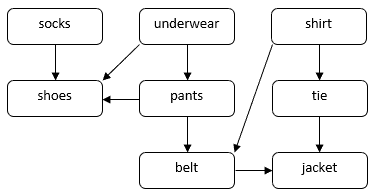
In this DAG, vertices correspond to garments. A direct edge in the DAG indicates that we need to put on garment before garment . Our task is to find an order to put on all garments while respecting the dependency constraints. For example, we can put on garments in the following order:

A topological sort of a DAG is a linear ordering of all its vertices such that if contains an edge , then appears before in the ordering. For a DAG, we can construct a topological sort with running time linear to the number of vertices plus the number of edges, which is .

3. Kahn’s Algorithm

In a DAG, any path between two vertices has a finite length as the graph does not contain a cycle. Let be the longest path from  (source vertex) to  (destination vertex). Since  is the longest path, there can be no incoming edge to . Therefore, a DAG contains at least one vertex that has no incoming edge.

3.1. Kahn’s Algorithm

In Kahn’s algorithm, we construct a topological sort on a DAG by finding vertices that have no incoming edges:

algorithm KahnsAlgorithm(G):
    // INPUT
    //   G = A Directed Acyclic Graph (DAG)
    // OUTPUT
    //   L = A topological sort of all vertices in G

    Compute in-degree for each vertex in G
    Initialize a queue Q with all vertices of in-degree 0
    
    Initialize an empty vertex list L

    while Q is not empty:
        u <- remove a vertex from Q
        add u to the end of L
        for each neighboring node v of u:
            decrease the in-degree of v by 1
            if the in-degree of v is 0:
                add v to Q

    return L

In this algorithm, we first compute the in-degree values for all vertices.

Then, we start with a vertex whose in-degree is 0 and put it into the end of the output list. Once we choose a vertex, we update the in-degree values of its adjacent vertices because the vertex and its out edges are removed from the graph.

We can repeat the above process until we choose all vertices. The output list is then a topological sort of the graph.

3.2. Time Complexity

To compute the in-degrees of all vertices, we need to visit all vertices and edges of . Therefore, the running time is  for in-degree calculations. To avoid computing these values again, we can use an array to keep track of the in-degree values of these vertices. Inside the while loop, we also need to visit all vertices and edges. Therefore, the overall running time is .

4. Depth First Search

We can also use a Depth First Search (DFS) algorithm to construct the topological sort.

4.1. Graph DFS with Recursion

Before we tackle the topological sort aspect with DFS, let’s start by reviewing a standard, recursive graph DFS traversal algorithm:

algorithm DFSTraversal(G):
    // INPUT
    //   G = A graph
    // OUTPUT
    //   L = A list of all vertices in G after DFS traversal

    L <- initialize an empty vertex list
    visited <- initialize an array to false for each vertex

    for each vertex u in G:
        if not visited[u]:
            dfsRecursive(u)

    return L

function dfsRecursive(u):
    visited[u] = true
    add u to the end of L
    for each neighboring vertex v of u:
        if not visited[v]:
            dfsRecursive(v)

In the standard DFS algorithm, we start with a random vertex in and mark this vertex as visited. Then, we recursively call the dfsRecursive function to visit all its unvisited adjacent vertices. In this way, we can visit all vertices of in  time.

However, since we’re putting each vertex into the list immediately when we visit it, and since we can start at any vertex, the standard DFS algorithm cannot guarantee to generate a topologically sorted list.

Let’s see what we need to do to address this shortcoming.

4.2. DFS Based Topological Sorting Algorithm

We can modify the DFS algorithm to generate a topological sort of a DAG. During the DFS traversal, after all neighbors of a vertex are visited, we then put it to the front of the result list . In this way, we can make sure that appears before all its neighbors in the sorted list:

algorithm DFSTopologicalSort(G):
    // INPUT
    //   G = A Directed Acyclic Graph (DAG)
    // OUTPUT
    //   L = A topological sort of all vertices in G

    L <- initialize an empty vertex list
    visited <- initialize an array to false for each vertex

    for each vertex u in G:
        if not visited[u]:
            topologicalSortRecursive(u)

    return L

function topologicalSortRecursive(u):
    visited[u] = true
    for each neighboring vertex v of u:
        if not visited[v]:
            topologicalSortRecursive(v)
    add u to the front of L

This algorithm is similar to the standard DFS algorithm. Although we still start with a random vertex, we don’t put the vertex into the list immediately once we visit it. Instead, we first visit all its neighbors recursively and then put the vertex to the front of the list. Therefore, if contains an edge , then appears before in the list.

The overall running time is also , as it has the same time complexity as the DFS algorithm.

5. Conclusion

In this article, we showed an example of topological sorting on a DAG. Also, we discussed two algorithms that can make a topological sort in time.

The Java implementation of the DFS based topological sorting algorithm is available in our article on Depth First Search in Java.