1. Overview
In this tutorial, we’ll talk about how eigenfaces work. First, we’ll describe the basic idea behind this method and present the algorithm in detail. Finally, we’ll focus on the pros and cons of this technique.
2. Basic Idea
Eigenfaces is a representation learning method in computer vision focusing on facial images. The goal of the method is to represent an image that depicts the face of a person as a linear combination of a set of basic images that are called eigenfaces.
Suppose all images representing a human face lie in a manifold in
. If we can find the optimal eigenfaces, we can represent any facial image as a linear combination.
So, the most important part is how to compute the eigenfaces. To do this, we need a large set of facial images to act as the training set. Then, based on this set, we try to choose the eigenfaces that capture the most useful variations in the appearance of the training facial images.
3. Algorithm
Here, let’s discuss the algorithm in more detail.
First, we have to collect a set of facial images. Then, we have to preprocess these images to reduce any kind of irrelevant variations.
The most common preprocessing step is to align the eyes, the nose, and the mouth. Then, we can also normalize the lightness and the pose of the images. It is very important to apply these preprocessing steps because they let the algorithm focus on the appearance-related regions of the image and disregard other irrelevant facial parts.
After preprocessing, we transform the images into a set of feature vectors that encode the visual information. The covariance matrix of these vectors corresponds to the correlations between the various features of the faces in our dataset. So, we’ll use the covariance matrix to get the eigenfaces.
More specifically, we compute the eigenvectors of the covariance matrix that span the latent space of the facial variations. These eigenvectors will then be used as the basis images of the eigenface representation of a new test facial image.
In the diagram below, we can see what the training pipeline looks like:

So, finally, to represent a new test facial image, we transform it into a feature vector and then project it into the space spanned by the eigenvectors. The projection coefficients represent the face as a linear combination of the eigenfaces.
In the diagram below, we can see what the test pipeline looks like:

Below, we can see an example of how an image is represented as a linear combination of the eigenfaces:
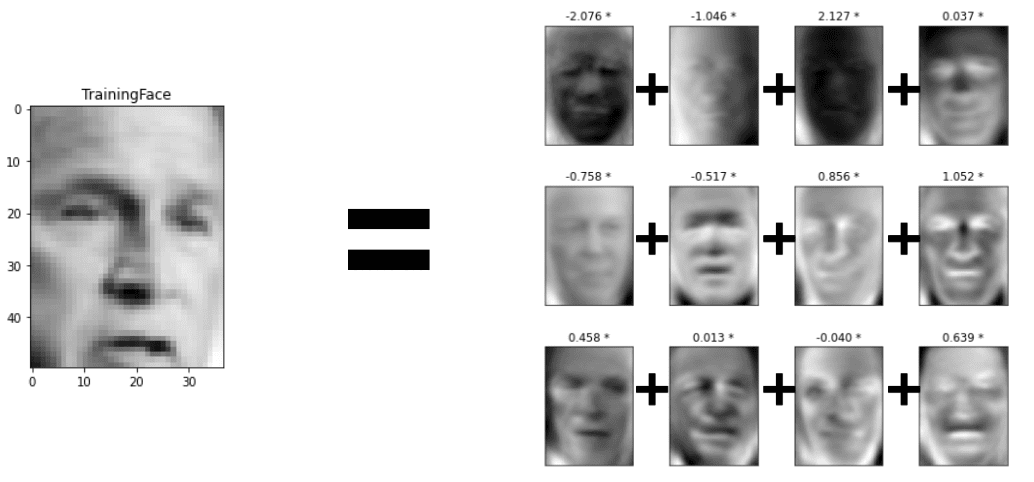
4. Advantages
Now, let’s discuss the key advantages of eigenfaces in representing facial images.
The most useful characteristic of eigenfaces is their efficiency and compactness. Specifically, the coefficients that are computed using the eigenvectors are very few since they are chosen to capture the most important variations in the appearance of faces. So, a new image can be represented using just a few numbers. This is very useful in a variety of applications like search engines and security systems.
Another advantage of this method is its robustness to lightning and pose variations which are very crucial in tasks like classification.
5. Limitations
Due to its simplicity, the method of eigenfaces presents some limitations.
Most importantly, eigenfaces are not robust enough to represent any kind of facial image. The method is very dependent on the quality of the training set. So, it can mainly represent faces similar to the ones in the training set. On the bright side, this characteristic is something that we can take into account in advance and collect a diverse enough training set.
6. Conclusions
In this article, we presented the method of eigenfaces. First, we discussed the algorithm behind this method and then its main advantages and disadvantages.