1. Introduction
Computer networks let us transfer data from one device to another. For a successful data transfer, it’s required that the target system receives the same data sent by the source system. However, data may get corrupted while being transferred from one node to another. Cyclic Redundancy Checks (CRC) and Checksums are two popular mechanisms to detect data corruption.
In this article, we’ll discuss these two popular techniques, how they work, and their merits and demerits.
2. Types of Errors
Data corruption errors are classified based on the number of bits altered during transmission. An alteration can happen due to interference, which can change the shape of the signal. These errors are classified into two categories.
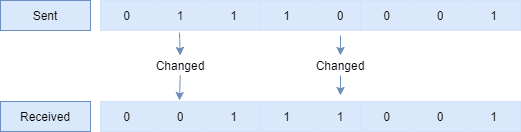
2.1. Single-Bit Error
A Single-Bit error occurs when there’s a change in one bit in a data byte:

2.2. Burst Error
A Burst error occurs when there’s a change in more than one bit in a data byte:
3. What’s a Cyclic Redundancy Check?
A Cyclic Redundancy Check (CRC) is an error-detecting code that lets us detect accidental changes to the transmitted data. Let’s define what these words refer to:
- Cyclic: based on cyclic codes from where CRC derives this term
- Redundancy: the check value that’s added to the data to verify its correctness
At its destination, the incoming data is divided by the check value (divisor). If the remainder is zero, then the data unit is assumed to be valid and accepted. A non-zero remainder indicates that data is corrupted and should be rejected. The CRC checker at the transmitter and the CRC generator at the receiver function the same.
3.1. How Does CRC Work?
CRC works based on the modulo-2 division, where addition is performed by an exclusive-OR operation. In an exclusive-OR operation, the subtraction operation is identical to the addition operation. This means adding two one bits results in 0, as in 1+1=0.
Besides, in CRC, a sequence of redundant bits is appended to the end of the transmitted data unit. This is also known as the CRC remainder. Thus, the resulting data unit becomes exactly divisible by a pre-determined binary number (divisor).
The divisor in the CRC generator is represented by an algebraic polynomial. A string of 0s and 1s are expressed as the polynomial with coefficients of 0 and 1. The power of each term in the polynomial refers to the position of the bit, and the corresponding coefficient reflects the value of the bit (0 or 1). A polynomial is represented by removing all terms with zero coefficients. Let’s explain the computation with an example for both the sender and receiver sides.
3.2. CRC Computation at Sender Side
In this example, we’ll encode a 14-bit message with a three-bit CRC, with a polynomial x3 + x + 1. A 3rd-degree polynomial has four coefficients (1x3 + 0x2 + 1x + 1). In this case, the coefficients are 1, 0, 1, and 1. The result of the calculation is three bits long.
Let’s start with the message that needs to be sent: 11010011101100
Here’s the first calculation for computing a three-bit CRC:
11010011101100 000 <--- Data padded by 3 bits of 0s on the right side 1011 <--- Divisor (4 bits) = x³ + x + 1 ------------------ 01100011101100 000 <--- Result
Now, let’s show the complete computation:
11010011101100 000 <--- Data padded by three bits of 0s on the right side
1011 <--- Divisor (four bits) = x³ + x + 1
01100011101100 000 <--- Result (First four bits are XORed with the divisor, rest of the bits are unchanged)
1011 <--- Divisor ...
00111011101100 000
1011
00010111101100 000
1011
00000001101100 000 <--- Divisor moves over to align with the next 1 in the dividend (since quotient for that step was zero)
1011
00000000110100 000
1011
00000000011000 000
1011
00000000001110 000
1011
00000000000101 000
101 1
-----------------
00000000000000 100 <--- remainder (three bits). Division algorithm stops here as dividend is equal to zero.
3.3. CRC Computation at Receiver Side
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.
11010011101100 100 <--- Input with the check value
1011 <--- Divisor
01100011101100 100 <--- Result
1011 <--- Divisor
00111011101100 100
......
00000000001110 100
1011
00000000000101 100
101 1
------------------
00000000000000 000 <--- Remainder
The remainder value 0 indicates the received data is correct and can be accepted.
Let’s now take an example where the received data has some transmission error and one bit has flipped. Thus, the exclusive-OR operation generates a non-zero remainder:
11010011101101 100 <--- input with check value
1011 <--- divisor
01100011101101 100 <--- result
1011 <--- divisor ...
00111011101101 100
......
00000000001111 100
1011
00000000000100 100
101 1
------------------
00000000000001 000
1 011
------------------
00000000000000 011 <--- remainder
4. What Is a Checksum?
A checksum is another error-detecting technique that validates the integrity of the transmitted data. A checksum value consists of a sequence of numbers and letters. To calculate a checksum, we run a program that puts that file through a hash function. The frequently used algorithms are MD5, SHA-1, SHA-256, and SHA-512.
The hash function takes the input and produces a string of a fixed length. For the same input, the hash function always returns the same checksum value. However, the checksum value varies greatly if there’s a slight change in the input data.
4.1. How to Calculate a Checksum?
There are several ways to calculate the checksum of a file. For instance, most programming languages provide APIs that can compute checksums. Most operating systems also offer utilities that can quickly compute the checksum value. For example, Linux provides the cksum utility to calculate the checksum of a file. In Windows, PowerShell provides the Get-FileHash command to calculate the checksum of a file:
Get-FileHash C:\baeldung\Hello.txt
The Get-FileHash output includes the algorithm name, the checksum value, and the file location:
Algorithm Hash Path
--------- ---- ----
SHA256 45356929829DC9FDED17E755DB91B93C25A4ED3FB9D60D92D4BD1E935A0ECC75 C:\baeldung\Hello.txt
The above PowerShell command calculates the checksum of the Hello.txt file. By default, it uses the SHA256 algorithm. To use another algorithm, we can specify it by using the -Algorithm argument:
Get-FileHash C:\baeldung\Hello.txt -Algorithm SHA512The get-FileHash output shows the modified algorithm name and the checksum value for the same file:
Algorithm Hash Path
--------- ---- ----
SHA512 3B6FC410AAC9453DF953A84E806FF789A88549AD35DBB6EA30C832AF32316AC4832... C:\baeldung\Hello.txt5. Summary
Let’s summarize the comparison between CRC and Checksum on various aspects:
| Area | CRC | Checksum |
|---|---|---|
| Purpose | To detect data transmission errors between source and target machines. | Software applications use the checksum to calculate data integrity |
| Error Detection | Capable of detecting double-digit errors | Can detect single-bit errors |
| Complexity | Uses complex functions to detect errors | Uses relatively less complex functions |
| Reliability | More reliable than a checksum due to the mathematical formula it employs to calculate the CRC | Less reliable than CRC |
| Existence | Relatively new – an improvement over checksum | The checksum is an old concept |
6. Conclusion
In this article, we discussed two major error-detecting techniques used during data transmission. First, we started with CRC and explained how it works. We then talked about Checksum and showed several means to calculate it.
Finally, we provided a quick summary of some key attributes of CRC and Checksum.