Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In computer science, a binary tree is a very popular and widely used data structure. It includes a root, a left child (or a subtree), and a right child (or a subtree). In addition, each node can have at most two child nodes, excluding the leaf nodes. Based on this principle, there can be many variations of it.
In this tutorial, we’ll discuss two popular variations of it: complete and almost complete binary tree.
In order to understand and differentiate a complete and almost complete binary tree, let’s start our discussion with the definition of a full binary tree.
A full binary tree is also known as 2-tree in which every node other than the leaf nodes has two child nodes. It means all the leaf nodes should be at the same level and all other internal nodes should contain two child nodes each.
Let’s see some examples:
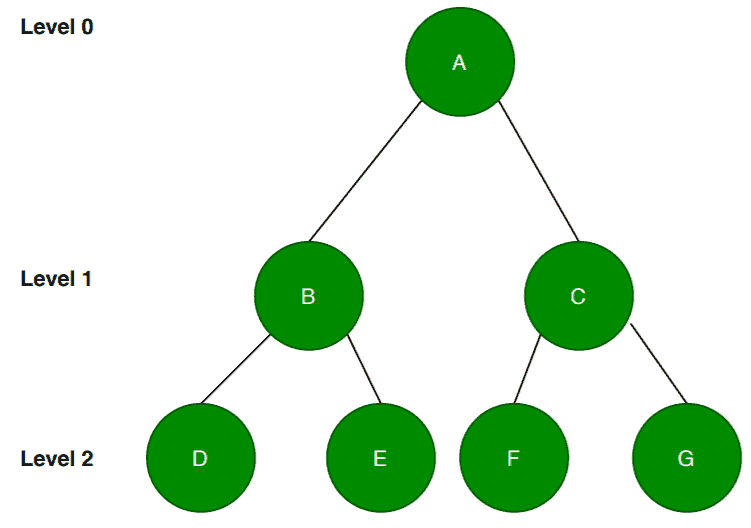
If we look at this tree, we can see that it has two nodes for all the internal nodes except the leaf nodes. In addition to that, all the leaf nodes are one the same level. Hence, we can say that this is an example of a full binary tree.
Let’s see another tree example:
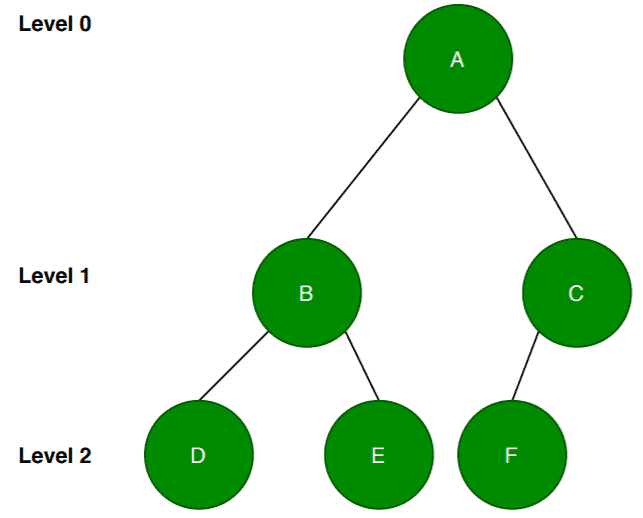
If we check this tree, the node is an internal node here and is not a leaf node. Although all the leaf nodes are on the same level, node
has only one child node which doesn’t satisfy the definition. Therefore, this example is not a full binary tree.
It follows the definition of a binary tree with some additional conditions. In a complete binary tree, all the levels of a tree are filled entirely except the last level. In the last level, nodes might or might not be filled fully. Also, let’s note that all the nodes should be filled from the left.
Now let’s try to simplify it. A complete binary tree has two child nodes at each level. In the definition, we mentioned all the levels are filled completely except at the last level. Let’s denote the level of a tree by . If a binary tree is completely filled then at each level we’ll have
nodes.
In our case, it is absolutely mandatory to contain nodes at each level except the last level.
Another point we mentioned in the definition is that we fill the nodes from the left. So it is not allowed for a node to have a right child node without having a left child node.
Now we know the theory, let’s verify the definition with the help of a couple of examples:
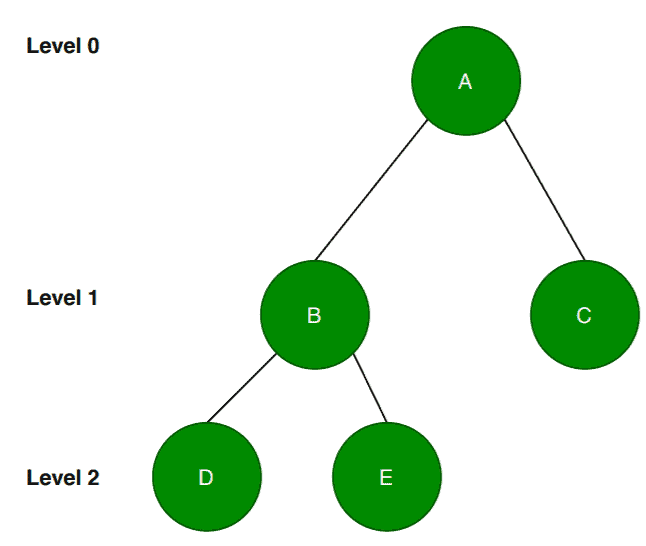
According to the definition, all the levels except the last level should be completely filled. Here, the level is the last level. The tree has the root node
at level
and two nodes
and
at level
. Till now, it satisfies the definition. Also, let’s note that the nodes are filled from the left.
At level , there are
nodes. But most importantly, the nodes are filled from left. Therefore we can conclude that it is a complete binary tree.
Let’s take another example:
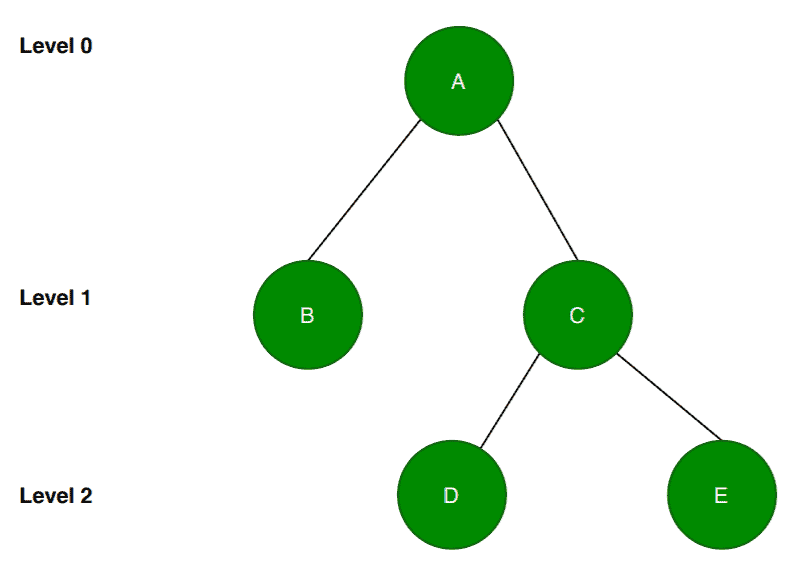
First, we’ll check if the given tree has the required number of nodes at each level except the last level which is level in this case. We can see that the given tree satisfies this condition.
Next, we’ll check whether the nodes are filled from the left or not. At level , the node
has no child nodes. That’s fine according to the definition.
But the problem with this tree is that the node has two child nodes. Now according to the definition, the nodes need to be filled from the left. So there should be a left child node for the node
which is missing here. Therefore, this example doesn’t follow the definition. Hence, it is not a complete binary tree.
We can use it in the heap data structure. In computer science, heaps can be of two types: max-heap and min-heap. Algorithms like Heap Sort uses it for sorting.
It is also used in implementing priority queues and external sorting algorithms.
An almost complete binary tree is a special kind of binary tree where insertion takes place level by level and from left to right order at each level and the last level is not filled fully always. It also contains nodes at each level except the last level.
The main point here is that if we want to insert any node at the lowest level of the tree, it should be inserted from the left. All the internal nodes should be completely filled.
An almost complete tree is also a complete binary tree.
Let’s take a couple of examples:
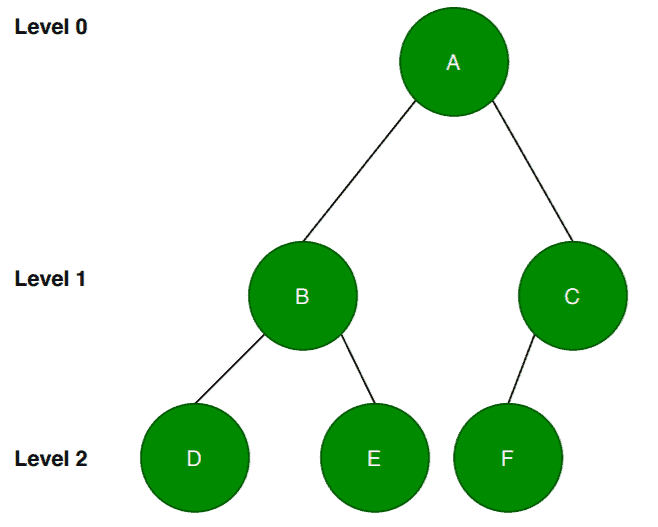
Notice that this example is the same as the first example of a full binary tree with the missing node . So here, we deleted the node
at the level
. At this point, if we observe, it satisfies the definition of a complete binary tree. The question is whether it is an almost complete binary tree?
The answer would be yes. Let’s discuss further. This example satisfies the definition as it has the required number of nodes at level and
. Level
is the last level here. Therefore, it is not required to have all the
nodes at level
.
Now, what is interesting to analyze is whether the nodes at the lowest level are present from left to the right direction or not. So here the node has two child nodes
and the node
has one child node
but most importantly it is left child node. Therefore it satisfies the definition of an almost complete binary tree.
Let’s take another example:
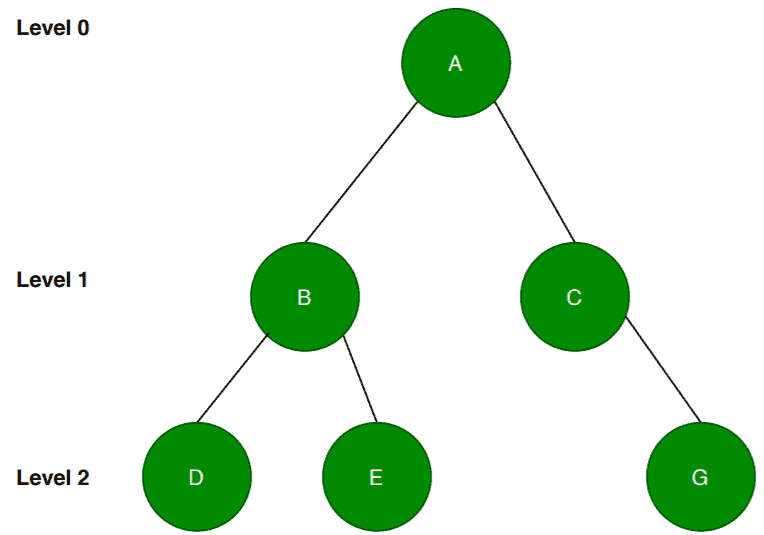
Again, notice that this is exactly the same as the first example but here we’ve deleted the node from the tree.
According to the definition, we should insert the nodes from left to right at each level. Here, in this case, we can see that the node doesn’t have any left child node. We deleted the left child although the node has a right child node. This is not allowed according to the definition.
Therefore, this is not an almost binary tree nor complete.
In this section, we’ll summarize all the points that we discuss so far and we’ll put all the information in a table:
| Parameter | Complete Binary Tree | Almost Complete Binary Tree |
|---|---|---|
| Definition | When the tree is complete then the last level might or might not be full. | In an almost complete binary tree the last level is not full for sure. |
| Property | A complete binary tree may or may not be an almost complete binary tree. | An almost complete binary tree will always be a complete binary tree. |
| Application | Heap data structure. | It doesn’t have any applications. If needed, a complete binary tree is used |
In this tutorial, we’ve discussed the concept of a complete and almost complete binary tree.
We also presented some differences between these two binary trees.