Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In Computer Science, a binary tree is a data structure in which each node has at most two children.
In this tutorial, we’ll show how to check if a binary tree is symmetric.
In a binary tree, each node has two subtrees, left subtree and right subtree. A subtree can be empty, a single node, or another binary tree. A binary tree is symmetric if the root node’s left subtree is a mirror reflection of the right subtree. For example, the following binary tree is symmetric:
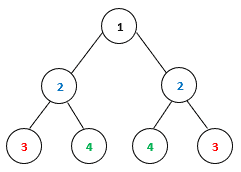
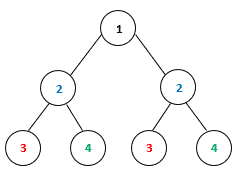
The following binary tree is not symmetric, although the two subtrees have the same tree structure:
Based on the symmetric definition, we can use the following rules to check whether two binary trees are a mirror reflection of each other:
It is easy to transform these conditions into a recursive algorithm:
algorithm isSymmetric(root):
// INPUT
// root = the root node of the binary tree
// OUTPUT
// Returns true if the binary tree is symmetric. Otherwise, returns false.
if root is empty:
return true
return isMirror(root.left, root.right)
function isMirror(root_1, root_2):
if root_1 is empty and root_2 is empty:
return true
else if root_1 is empty or root_2 is empty:
return false
else:
return root_1.value = root_2.value and
isMirror(root_1.left, root_2.right) and
isMirror(root_1.right, root_2.left)In this algorithm, we use a recursive function, , to check whether two binary trees are a mirror reflection of each other. Firstly, we do some sanity checks to handle cases where at least one of the input binary trees is empty. Then, we apply the symmetric rules on the two non-empty trees by recursively calling the
function.
At the high level, we can call the function on our input binary tree’s left subtree and right subtree. Since we traverse the entire input tree once, the running time of this algorithm is
, where
is the total number of nodes in the tree.
We can also solve this problem in an iterative way by traversing the binary tree level by level. At each level, the tree nodes should be symmetric:
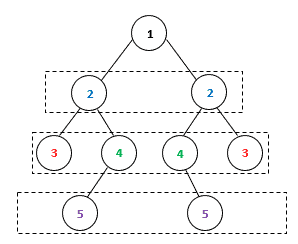
We can implement this tree traversal algorithm with the help of a queue data structure:
algorithm isSymmetric(root):
// INPUT
// root = the root node of the binary tree
// OUTPUT
// Returns true if the binary tree is symmetric. Otherwise, returns false.
if root is empty:
return true
q <- construct a tree node queue
q.add(root.left)
q.add(root.right)
while q is not empty:
root_1 <- q.pop()
root_2 <- q.pop()
if root_1 is empty and root_2 is empty:
continue
else if root_1 is empty or root_2 is empty:
return false
else if root_1.value != root_2.value:
return false
q.add(root_1.left)
q.add(root_2.right)
q.add(root_1.right)
q.add(root_2.left)
return true
In this iterative algorithm, we first construct a queue that contains the two children of the root node. Then, in each iteration of the loop, we extract two nodes from the queue and compare their values. Also, the right and left children of the two nodes are inserted in the queue in the opposite order for future symmetric detections. We continue this process until we traverse all tree nodes or we detect that the tree is not symmetric.
Same as the recursive solution, we also traverse the entire input tree once. Therefore, the running time of the iterative algorithm is , where
is the total number of nodes in the tree.
In this tutorial, we showed some examples of symmetric binary trees. Also, we discussed two algorithms that can detect whether a binary tree is symmetric in linear time.