Check if a Binary Number Is Divisible by 3 | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll explore several ways to check whether a binary number is divisible by three.

First, we’ll show how to accomplish it by converting binary into decimal numbers. Then, we’ll see how to check by counting odd and even digits. Finally, we’ll explore how to create our own Deterministic Finite Automaton to check if a binary number is divisible by three.

2. Converting to Base 10

One way to determine whether a binary number is divisible by three is to first convert it to a decimal number (base 10) and then check if such a number is divisible by three.

For example, let’s take the binary number 1100101101 and convert it to a decimal number:

1100101101 = (1 * 2^0) + (0 * 2^1) + (1 * 2^2) + (1 * 2^3) + (0 * 2^4) + (1 * 2^5) + (0 * 2^6)
                 + (0 * 2^7) + (1 * 2^8) + (1 * 2^9) 
1100101101 = 1 + 0 + 4 + 8 + 0 + 32 + 0 + 0 + 256 + 512
1100101101 = 813

Let’s go over the conversion steps. Starting with the rightmost digit, we multiplied each digit with its position’s power of two, starting with the exponent zero and increasing it by one for each following digit. To get the final value, we summed up the multiplication results. Accordingly 813 corresponds to the binary number 1100101101.

Going further, we’ll check whether the given number is divisible by three using the divisibility rule. The rule says that a decimal number is divisible by three if the sum of its digits is also divisible by three.

Thus, we can add the digits of the 813 as 8 + 1 + 3, which equals 12. Therefore, 813 is divisible by three, giving 271 as the result.

3. Counting Odd and Even Digits

Another way we can check if a binary number is divisible by three is by applying a rule similar to the one for checking whether the decimal number is divisible by 11. The rule states that a decimal number is divisible by 11 if the alternating difference and sum of its digits, processed from left to right, is divisible by 11. This same pattern applies to binary numbers for testing divisibility by three.

Next, let’s apply and test the rule using the binary representation of the number 46, which is 00101110. We’ll alternate between subtracting and adding the digits:

x <- 0 - 0 + 1 - 0 + 1 - 1 + 1 - 0 
x <- 2

As a result, we obtained the number two, which is not divisible by three. Therefore, the number 00101110 isn’t divisible by three.

Moreover, we can rewrite the formula to specifically count the ones in the odd and even positions in the number. If the difference between the counts is zero or divisible by three, then the number is divisible by three.

Next, let’s check whether the 00101110 is divisible by three by counting odds and even digits:

count the odd non-zero digits: 
    x <- 1 + 1 + 1 
    x <- 3
count the even non-zero digits:
    y <- 1
subtract the results:
    z <- x - y
    z <- 3 - 1
    z <- 2

Again we got a number that isn’t divisible by three, which means 00101110 isn’t divisible by three.

4. Using Deterministic Finite Automaton

Lastly, let’s see how to achieve the same functionality using the Deterministic Finite Automaton, or DFA for short. At a high level, DFA represents an abstract model that accepts or rejects a given string of symbols by running through a state sequence determined by the string.

It consists of:

Finite set of states ( $Q$ )
A finite set of input symbols ( $\Sigma$ )
Transition function ( $\delta$ )
The initial state ( $q_0$ )
A final (accepting) state ( $F$ )

When given an input string, a DFA traverses through its states based on the transitions dictated by the input symbols. The transition function tells us where to move next based on the current state and the input symbol. If the DFA ends up in an accepting state after processing the entire input string, the string is accepted; otherwise, it’s rejected.

Let’s construct a DFA to recognize binary numbers divisible by three.

It’ll have three states, each representing one of the possible remainder outcomes, 0, 1, or 2:

Since we’re dealing with binary numbers, the input symbols will be 0 and 1:

4.1. Constructing Transition Table

One way to represent the transition function is by using a transition table. To fill the transition table, let’s calculate the next state for each state based on the input symbol.

If the current state is $q_i mod 3$ and the input symbol is zero, we’ll move to state $(2 * q_i) mod 3$ . This is because when we append zero to a binary string, the value doubles:

x <- 2x

// example
11 (decimal 3) -> 110 (decimal 6)

Similarly, if the input symbol is one, we’ll move to the state $(2 * q_i + 1) mod 3$ . When we concatenate one to a binary string, the value doubles and increases by one:

x <- 2x + 1

// example
11 (decimal 3) -> 111 (decimal 7)

Based on these facts, to calculate the next state $q_j$ , we’ll use the function:

Let’s explore its components:

$q_i$ represents the current state
$x$ represents the input symbol
$q_j$ represents the next state

Now, let’s see how to determine the next state if the current state quals zero and the input symbol is one:

δ(0, 1) <- (2 * 0 + 1) mod 3
δ(0, 1) <- 1

The calculated result implies that, given the current state ( $q_0$ ) and the input ( $x = 1$ ), we need to move to state one ( $q_1$ ).

Using the same method, we can populate the entire table:

Current State	Next State for Input 0 (x=0)	Next State for Input 1 (x=1)
q₀ (0)	q₀	q₁
q₁ (1)	q₂	q₀
q₂ (2)	q₁	q₂

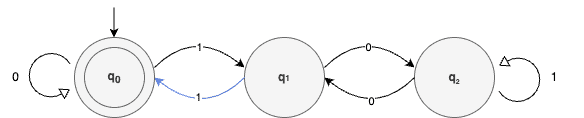
4.2. Constructing Transition Diagram

Next, based on the calculated values, let’s create a state diagram:

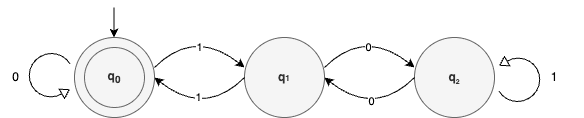
Each node represents one of the states. Arrows illustrate transitions from one state to another based on the input value.

Our starting point will be q₀, regardless of the digit we’re beginning with. Moreover, the same state will act like the final (accepting) state since it represents the state when the remainder is zero, which indicates a given number is divisible by three.

4.3. Divisibility Test

Now that we’ve explored the theory, let’s check whether our DFA works correctly. Let’s use the binary number 1001 as an example. It represents the number nine in a decimal system. Additionally, the automaton reads the input from left to right.

We’ll start the process with q₀, which represents the initial state. The first digit is one, so we’ll move to q₁:

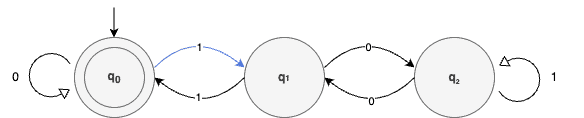
Our next digit is zero, which requires us to shift from q₁ to q₂:

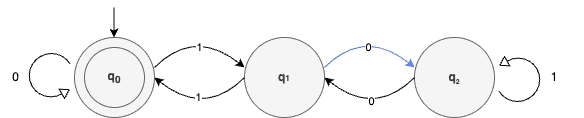
Then, because the next digit is zero, we need to go back to q₁:

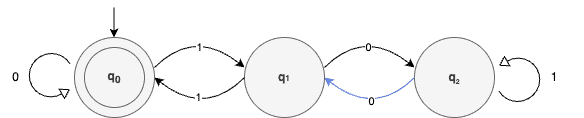
Finally, the last digit is one, moving us back to the initial position, which is also our accepting state:

We can create DFA to test divisibility by other numbers in a similar manner. The only difference would be in the number of states DFA would have.

5. Conclusion

In this article, we learned how to use different ways to determine whether a binary number is divisible by three.

To sum up, one way to achieve this is to convert the binary number into a decimal number and then use the divisibility by three rule. It’s also possible to achieve the same functionality by counting the odd and even ones in the number and comparing their differences. Finally, creating the DFA is another way we can use to check whether the binary number is divisible by three.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex