Batch Normalization in Convolutional Neural Networks

1. Introduction

Training Deep Neural Networks is a difficult task that involves several problems to tackle. Despite their huge potential, they can be slow and be prone to overfitting. Thus, studies on methods to solve these problems are constant in Deep Learning research.

Batch Normalization – commonly abbreviated as Batch Norm – is one of these methods. Currently, it is a widely used technique in the field of Deep Learning. It improves the learning speed of Neural Networks and provides regularization, avoiding overfitting.

But why is it so important? How does it work? Furthermore, how can it be applied to non-regular networks such as Convolutional Neural Networks?

2. Normalization

To fully understand how Batch Norm works and why it is important, let’s start by talking about normalization.

Normalization is a pre-processing technique used to standardize data. In other words, having different sources of data inside the same range. Not normalizing the data before training can cause problems in our network, making it drastically harder to train and decrease its learning speed.

For example, imagine we have a car rental service. Firstly, we want to predict a fair price for each car based on competitors’ data. We have two features per car: the age in years and the total amount of kilometers it has been driven for. These can have very different ranges, ranging from 0 to 30 years, while distance could go from 0 up to hundreds of thousands of kilometers. We don’t want features to have these differences in ranges, as the value with the higher range might bias our models into giving them inflated importance.

There are two main methods to normalize our data. The most straightforward method is to scale it to a range from 0 to 1:

$x_{normalized}=\frac{x - m}{x_{max} - x_{min}}$

$x$ the data point to normalize, $m$ the mean of the data set, $x_{max}$ the highest value, and $x_{min}$ the lowest value. This technique is generally used in the inputs of the data. The non-normalized data points with wide ranges can cause instability in Neural Networks. The relatively large inputs can cascade down to the layers, causing problems such as exploding gradients.

The other technique used to normalize data is forcing the data points to have a mean of 0 and a standard deviation of 1, using the following formula:

$x_{normalized}=\frac{x - m}{s}$

being $x$ the data point to normalize, $m$ the mean of the data set, and $s$ the standard deviation of the data set. Now, each data point mimics a standard normal distribution. Having all the features on this scale, none of them will have a bias, and therefore, our models will learn better.

In Batch Norm, we use this last technique to normalize batches of data inside the network itself.

3. Batch Normalization

Batch Norm is a normalization technique done between the layers of a Neural Network instead of in the raw data. It is done along mini-batches instead of the full data set. It serves to speed up training and use higher learning rates, making learning easier.

Following the technique explained in the previous section, we can define the normalization formula of Batch Norm as:

$z^N = \left( \frac{z - m_z}{s_z} \right)$

being $m_z$ the mean of the neurons’ output and $s_z$ the standard deviation of the neurons’ output.

3.1. How Is It Applied?

In the following image, we can see a regular feed-forward Neural Network: $x_i$ are the inputs, $z$ the output of the neurons, $a$ the output of the activation functions, and $y$ the output of the network:

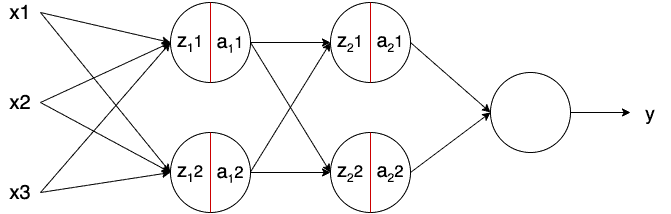
Batch Norm – in the image represented with a red line – is applied to the neurons’ output just before applying the activation function. Usually, a neuron without Batch Norm would be computed as follows:

$z = g(w, x) + b; \hspace{1cm} a = f(z)$

being $g()$ the linear transformation of the neuron, $w$ the weights of the neuron, $b$ the bias of the neurons, and $f()$ the activation function. The model learns the parameters $w$ and $b$ . Adding Batch Norm, it looks as:

$z = g(w, x); \hspace{1cm} z^N = \left( \frac{z - m_z}{s_z} \right) \cdot \gamma + \beta; \hspace{1cm} a = f(z^N)$

being $z^N$ the output of Batch Norm, $m_z$ the mean of the neurons’ output, $s_z$ the standard deviation of the output of the neurons, and $\gamma$ and $\beta$ learning parameters of Batch Norm. Note that the bias of the neurons ( $b$ ) is removed. This is because as we subtract the mean $m_z$ , any constant over the values of $z$ – such as $b$ – can be ignored as it will be subtracted by itself.

The parameters $\beta$ and $\gamma$ shift the mean and standard deviation, respectively. Thus, the outputs of Batch Norm over a layer results in a distribution with a mean $\beta$ and a standard deviation of $\gamma$ . These values are learned over epochs and the other learning parameters, such as the weights of the neurons, aiming to decrease the loss of the model.

3.2. Implementation in Python

Implementing Batch Norm is quite straightforward when using modern Machine Learning frameworks such as Keras, Tensorflow, or Pytorch. They come with the most commonly used methods and are generally up to date with state of the art.

With Keras, we can implement a really simple feed-forward Neural Network with Batch Norm as:

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, BatchNormalization

model = Sequential([
    Dense(16, input_shape=(1,5), activation='relu'),
    BatchNormalization(),
    Dense(32, activation='relu'),
    BatchNormalization(),
    Dense(2, activation='softmax')
])

3.3. Why Does Batch Normalization Work?

Now that we know how to apply and implement Batch Norm, why does it work? How can it speed up training and make learning easier?

There are different reasons why it is believed that Batch Norm affects all of that. Here we will expose the intuitions of the most important reasons.

Firstly, we can see how normalizing the inputs to take on a similar range of values can speed up learning. One simple intuition is that Batch Norm is doing a similar thing with the values in the layers of the network, not only in the inputs.

Secondly, in their original paper Sergey et al. claim that Batch Norm reduces the internal covariate shift of the network. The covariate shift is a change in data distribution. For example, going back to our example on the car rental service, imagine we want to include other motorbikes. If we only look at our previous data set, containing only cars, our model will likely fail to predict motorbikes’ price. This change in data (now containing motorbikes) is named covariate shift, and it is gaining attention as it is a common issue in real-world problems.

The internal covariate shift is a change in the input distribution of an internal layer of a Neural Network. For the neurons in an internal layer, the inputs received (from the previous layer) are constantly changing. This is due to the multiple computations done before it and the weights over the training process.

Applying Batch Norm ensures that the mean and standard deviation of the layer inputs will always remain the same; $\beta$ and $\gamma$ , respectively. Thus, the amount of change in the distribution of the input of layers is reduced. The deeper layers have a more robust ground on what the input values are going to be, which helps during the learning process.

Lastly, it seems that Batch Norm has a regularization effect. Because it is computed over mini-batches and not the entire data set, the model’s data distribution sees each time has some noise. This can act as a regularizer, which can help overcome overfitting and help learn better. However, the noise added is quite small. Thus, it generally is not enough to properly regularize on its own and is normally used along with Dropout.

4. Batch Normalization in Convolutional Neural Networks

Batch Norm works in a very similar way in Convolutional Neural Networks. Although we could do it in the same way as before, we have to follow the convolutional property.

In convolutions, we have shared filters that go along the feature maps of the input (in images, the feature map is generally the height and width). These filters are the same on every feature map. It is then reasonable to normalize the output, in the same way, sharing it over the feature maps.

In other words, this means that the parameters used to normalize are calculated along with each entire feature map. In a regular Batch Norm, each feature would have a different mean and standard deviation. Here, each feature map will have a single mean and standard deviation, used on all the features it contains.

4.1. Implementation in Python

Again, implementing Batch Norm in Convolutional Neural Networks is really easy using modern frameworks. It does the operation in the background, using the same function we used before:

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, BatchNormalization, Conv2D, MaxPooling2D

model = Sequential([
  Conv2D(32, (3,3), input_shape=(28, 28, 3) activation='relu'), 
  BatchNormalization(),
  Conv2D(32, (3,3), activation='relu'), 
  BatchNormalization(),
  MaxPooling2D(),
  Dense(2, activation='softmax')
])

5. Conclusion

Here, we’ve seen how to apply Batch Normalization into feed-forward Neural Networks and Convolutional Neural Networks. We’ve also explored how and why does it improve our models and our learning speed.

Lastly, we’ve seen some simple implementations of this method using a modern Machine Learning framework such as Keras.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex