LazyList in Scala

1. Overview

The List is a standard data structure present in almost every programming language. However, the name sometimes means slightly different things in different languages. This article discusses functional lists with a constructor and two primary operations, head() and tail().

Functional lists have strict and lazy varieties. Laziness is essential because it allows us to represent infinite computations in a computer with limited resources.

For example, if we represent the Fibonacci numbers as a list using the strict variant, the application will compute the list until it runs out of memory and crashes:

def fibonacci(current: Int = 0, next: Int = 1): SimpleList[Int] = :@:(current, fibonacci(next, current + 1))

In this tutorial, we’ll understand the difference between Scala’s Lazy and strict lists and how we can use laziness in our favor to implement some algorithms more concisely than if we use the strict variant.

2. Functional Lists

Functional programming languages strongly influence Scala, clearly visible in its immutable, recursively defined lists:

sealed trait SimpleList[+T] {
  def empty: Boolean
  def head: T
  def tail: SimpleList[T]
}

case object SNil extends SimpleList[Nothing] {
  override def head = throw new IllegalArgumentException("Head of empty list")
  override def tail = throw new IllegalArgumentException("Tail of empty list")
  override val empty: Boolean = true
}

case class :@:[T](head: T, tail: SimpleList[T]) extends SimpleList[T] {
  override val empty: Boolean = true
}

We can visualize a constructed list with its two operations and see how strictness prevents us from using the simple representation of Fibonacci numbers we discussed before:

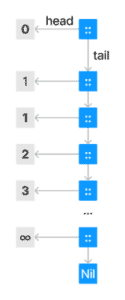
However, we can use Scala’s Baeldung Scala call-by-name semantics to delay the evaluation of the elements of the list until it’s absolutely necessary, which might never be.

3. When Laziness Is a Virtue

As we mentioned in the overview, using this version to implement the Fibonacci number generator will result in a stack overflow error. But as we know, Scala supports call-by-name semantics, and we can use them to implement the concept of infinite sequences.

Unfortunately, case class parameters can’t use by-name semantics. Hence, the lazy implementation needs some extra work to keep the convenience of pattern matching, and creating an instance without using the new keyword.

Therefore, the additional companion object with the apply and unapply methods:

sealed trait SimpleLazyList[+T] {
  def empty: Boolean
  def head: T
  def tail: SimpleLazyList[T]

  def ::[S >: T](e: S): SimpleLazyList[S] = #:@:(e, this)
}

case object SLNil extends SimpleLazyList[Nothing] {
  override def head = throw new IllegalArgumentException("Head of empty list")
  override def tail = throw new IllegalArgumentException("Tail of empty list")
  override val empty: Boolean = true
}

class #:@:[T](_head: => T, _tail: => SimpleLazyList[T]) extends SimpleLazyList[T] {
  override val empty: Boolean = true
  override lazy val head: T = _head
  override lazy val tail: SimpleLazyList[T] = _tail
}

object #:@: {
  def apply[T](head: => T, tail: => SimpleLazyList[T]) = new #:@:(head, tail)
  def unapply[T](slcons: #:@:[T]): Option[(T, SimpleLazyList[T])] = Some((slcons.head, slcons.tail))
}

The representation of a simple lazy List then looks like this:

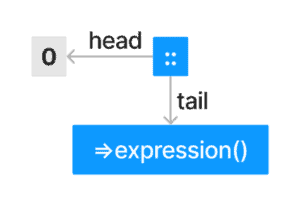
The above is enough to enable us to implement the Fibonacci series using the list, and it doesn’t result in stack overflow errors:

def fibonacci(current: Int = 0, next: Int = 1): SimpleLazyList[Int] = #:@:(current, fibonacci(next, current + next))
assertResult(8)(fibonacci().!!(7))

4. Scala’s LazyList

Scala’s LazyList is more complex than the minimal implementation we wrote for this tutorial. Still, the extra complexity is either to provide convenience or better performance while the fundamentals remain the same.

For example, our simple implementation can create performance problems in code that access it repeatedly because every time the tail is accessed, the program will recompute it.

We can correct this using a lazy value to ensure computation happens only on the first access.

Pre-2.13 versions of Scala had a class called Stream. We can understand LazyList as a rename of Stream, with one crucial difference: LazyList’s head is lazy while Stream‘s head is strict.

Also, its methods (for example, filter, map, and flatMap) are implemented in a way that avoids evaluating the head:

"The head of a Scala Lazy List is lazy" in {
  var side = "No side effect"
  val list =
    {
      side = "Side effect"
      side
    } #:: LazyList.empty
  assertResult("No side effect")(side)

  list.map(x => {
    side = "Another side effect"
    x.toUpperCase
  })
  assertResult("No side effect")(side)

  list.filter(x => x.startsWith("Side"))
  assertResult("No side effect")(side)

  println(list.head)
  assertResult("Side effect")(side)
}

5. Conclusion

In this tutorial, we explored how to write a minimal lazy functional list in Scala and use a lazy list to represent infinite series like the Fibonacci numbers.

We also learned the essential differences between our minimal list and Scala’s LazyList implementation, including that Scala’s implementation is lazy from head to tail, and it implements standard methods like filter and map in a way that avoids unnecessary evaluation. In addition, we learned that Scala versions before 2.13 had a class called Stream with similar semantics but with a strict head.

As always, the complete source code of the article is available over on GitHub.