Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: February 28, 2025
In this tutorial, we’ll introduce the triplet loss function.
First, we’ll describe the intuition behind this loss and then define the function and the training procedure. Finally, we’ll present some applications of triple loss and its challenges.
The triple loss function is a famous training objective in tasks like image retrieval, face recognition, text similarity, etc. However, before defining the process, let’s first talk about the intuition behind it by considering the example of face recognition.
So, let’s suppose that we want to implement a machine-learning system that recognizes faces. The network’s input is an image depicting a human face, and the output is the person’s identity in the image. To train our network, we have a dataset of face images.
A simple solution could be to handle the task as a pure classification task and train the network using the cross-entropy loss and the person’s identity in each image as the label. However, there are two problems with this solution:
In the image below, we can see a diagram of the above classification network:

We have to transform our classification task into a similarity learning task to deal with the above problems. In this case, the goal of the system is to measure the similarity of two given images.
So, during inference, the network takes a facial image, computes its similarity with a saved image of each subject, and outputs the identity with the highest similarity. In this case, to include an extra identity, we just have to keep a saved image with the new identity to compare with.
In the image below, we can see what the similarity network looks like:

Now, to train this similarity learning network, we need a loss function that considers the similarity of the input sample. This is where the famous triplet loss function appears.
Formally, the triplet loss is a distance-based loss function that aims to learn embeddings that are closer for similar input data and farther for dissimilar ones.
First, we have to compute triplets of data that consist of the following:
Then, the goal of the loss function is to learn embeddings such that the distance between the anchor and the positive example is smaller than the distance between the anchor and the negative example. More formally, this is defined as follows:
where is a distance metric (usually euclidean distance) and
is a hyperparameter that controls the minimum distance. When
, then
since the restriction of the margin is not violated.
In the image below, we can see a diagram of the triplet loss learning objective:
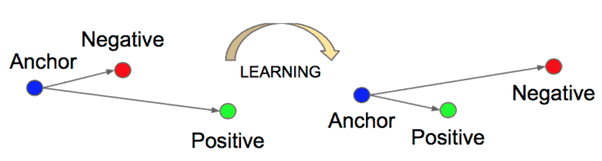
As we mentioned previously, face recognition is the most famous application of the triplet loss function. Now, let’s present some more applications.
We can use the triplet loss function in anomaly detection applications where our goal is to detect anomalies in real-time data streams. Using similarity learning, we can learn a representation of normal behavior and compute the similarity of each input sample with a normal one.
Similarity learning can also be used in information retrieval systems where the goal is to retrieve relevant documents to an input query text. We can learn a representation of each document by bringing the features of similar documents closer and the features of dissimilar documents further.
Finally, another useful application of the triplet loss function is in the recommendation systems. For example, suppose we want to recommend similar products to customers based on their previous purchases. In that case, we can train a similarity network using the triplet loss that computes the similarity of products.
Despite its huge success, the triplet loss functions present some challenges that we should always take into account when implementing similarity learning networks.
An important aspect of triplet loss is how to choose the right triplets. Specifically, we can easily observe that in the majority of data, the triple loss condition will already hold (the distance between the anchor and the negative example will be higher than the distance between the anchor and the positive example plus the margin). So, finding a way to get the triplets that do not satisfy this condition and help the network learn is very crucial.
Training a network using the triplet loss function is time-consuming and resource-intensive since we usually need large-scale datasets in order to learn robust similarity features.
In this article, we talked about the triplet loss function. First, we discussed the intuition and the definition of the loss function. Then, we briefly mentioned some of its applications and challenges.