Array Implementation of Stacks

1. Introduction

There are several possible implementations of the stack data structure, based on fixed-size arrays, dynamic arrays, and linked lists.

In this tutorial, we’ll implement the stack using the fixed-size array representation.

2. Fixed-size Array Representation

In this representation, the stack effectively consists of the following data:

• – the fixed-size array for keeping the stack elements
• – an integer counter holding the index of the stack’s top element
• – an integer value that defines the size of the array

In our discussion, we assume the array to be 1-indexed. So, the first inserted element of the stack has index 1. Similarly, the last inserted element has an index equal to the .

Let’s go over the process of stack modification so we understand how the implementation operates. Assume we have an empty stack of integers with :

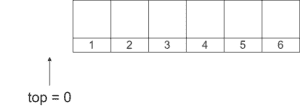
Let’s add integer 11 to the stack:

Next, we add two more integers, 7 and 25, to the stack. Note how changes according to the elements added:

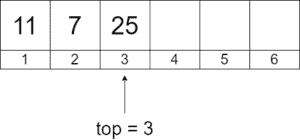
Finally, we remove the top element of the stack and get the following stack. Note that we do nothing with the element previously pointed by the top (25 in this case). We only update the counter, and the previous top element will just get overwritten by a new value when new elements are added to the stack:

We ignore adding new elements to the stack when it’s full. Similarly, we do nothing when requests to remove elements and the stack is empty. Practically, it’s worth adding error-handling logic in these situations.

3. Stack Operations and Pseudocodes

Now, we’ll show how to implement the stack operations using the fixed-size array representation. The pseudocodes are short and easy to understand. Additionally, it’s straightforward to translate the pseudocodes to a programming language implementation.

3.1. Push

Below we can find the pseudocode of the push operation. The operation first checks if there’s a space for the new element. Then, it updates the top counter and adds the new element on top of the

stack:

algorithm PUSH(S, a):
    // INPUT
    //    S = a stack
    //    a = the element to be added to the stack
    // OUTPUT 
    //    The element is added on top of the stack

    if the stack S is full:
        report an error or log the problem
        return
    S.top <- S.top + 1
    S.elements[S.top] <- a

3.2. Pop

The pop operation’s logic is the opposite of push. First, it checks if there’re elements in the stack. Then, it updates the top counter to show the new top element of the stack:

algorithm POP(S):
    // INPUT: 
    //    S = a stack
    // OUTPUT: 
    //    The top element of the stack is removed

    if the stack S is empty:
        report an error or log the problem
        return

    element <- S[S.top]
    S.top <- S.top - 1
    
    return element

3.3. Top

Top simply returns the top element of the stack:

algorithm TOP(S):
    // INPUT: 
    //    S = a stack
    // OUTPUT: 
    //    Returns the top element of the stack
    //    or null if the stack is empty.
    
    if the stack S is empty:
        report an error or log the problem
        return null
    
    return S.elements[S.top]

3.4. Empty

To check if the stack contains any elements, the empty operation is used:

algorithm EMPTY(S):
    // INPUT: 
    //    S = a stack
    // OUTPUT: 
    //    Returns true if the stack is empty, false otherwise
    
    if S.top = 0:
        return true
    
    return false

3.5. Full

The full operation checks another boundary condition – whether the stack is full and can’t accept new elements to be added:

algorithm FULL(S):
    // INPUT: 
    //    S = a stack
    // OUTPUT: 
    //    Returns true if the stack is full, false otherwise
    
    if S.top = S.capacity:
        return true
    
    return false

4. Strengths and Weaknesses of the Implementation

The immediate benefit of the implementation is its easiness – it’s quite straightforward to understand and implement. Another benefit is the restriction on the number of elements that can be put into the stack. Consequently, the implementation naturally fits applications where the stack size needs to be limited.

On the other hand, the same feature of the limited size introduces a weakness – the implementation is hard to use for cases when the elements count is variable and isn’t known beforehand. In this case, reserving a big chunk of memory may be redundant. Contrarily, reserving a small chunk of memory may cause the to stack run out of memory, and we may have to use multiple stacks. Dynamic array and linked list implementations don’t have this limitation as they grow their capacity as needed.

5. Conclusion

In this topic, we’ve presented the fixed-size array representation of stacks. Additionally, we’ve provided the pseudocodes for the operations of the stack based on the representation. Finally, we’ve pointed out the strengths and weaknesses of the implementation.