1. Introduction
The singly linked list is a common data structure implemented in most high-level programming languages. For instance, these are implementations of singly linked lists:
- C++ STL type std::foward_list
- Scala and F# type List
In its most basic form, a linked list consists of a collection of nodes. Each node contains data and a reference to the next node.
In this tutorial, we’ll learn how to find the 
th element of the singly linked list by traversing through the list.
2. Algorithm to Find the nth Element
We are interested in implementing a function that gets the th element of a linked list. How might we write such a function? To get the th element, we must traverse through the list.
We introduce an algorithm for getting the element with index , 
of a singly linked list. In the subsequent section, we shall go over each of the important steps in a structured manner.
Consider the following pseudo-code:
algorithm GetItem(head, n):
// INPUT
// head = the reference to the linked list
// n = the index of the node to be fetched
// OUTPUT
// Returns the data of the node at index n
current <- head
i <- 0
// Iterate until the end of the linked list
while current != null:
if i = n:
// We finished counting to n and are done
return current.data
// Move current to the next successive node
current <- current.next
// Increase the counter by 1
i <- i + 13. A Walk-Through of GetItem(Head,n)
We begin at the head of the linked list.
Our initial setup is as follows:
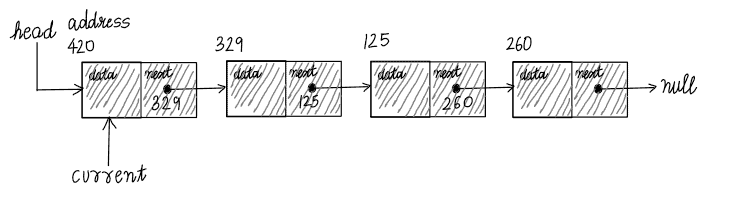
We take an empty pointer current and set it to refer to the head node – the 
st node of the linked list. current always refers to our current position in the linked list.
current.next points to the successive node – the 
nd node of the linked list. If we assign current = current.next, this will move current to the right. The below snap is just after current is moved to the right:
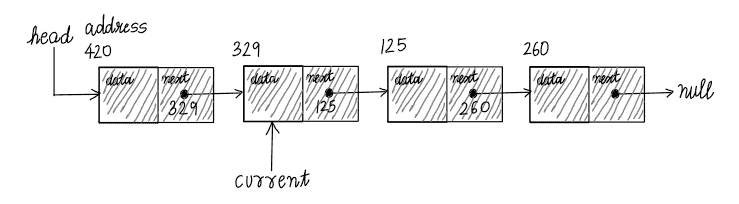
Executing current = current.next multiple times in a while loop allows us to traverse through the linked list. However, we must be careful not to go beyond the end of the linked list. If current = null, invoking current = current.next on a null object will cause our program to crash. So, we write the boundary condition current!=null to control the maximum number of iterations.
The logic so far helps us move through the list. However, it would be good to keep a track of the index we are at. Hence, we use a counter-variable i and count to n. First, we initialize i=0, and inside each iteration, we check if the counter i equals n. If this condition is true, we return the data inside the current node to the caller function. If false, we proceed with the next iteration, moving current to the next successive node and increasing the value of the counter variable i by .
If the control reaches the statement following the end of the while-loop, it implies that we have reached the end of the list before counting to n.
4. Algorithm to Find the nth Element From the Tail of the List
We can build upon the above basic technique to find the th element from the end of the singly linked list. To be consistent, we use the following convention. We shall refer to the tail of the linked list as the element having index 
, the last but one element as having index 
, and so forth.
We are interested in writing a function that takes the head of the linked list as the first argument and an index (
) as the second argument.
Consider the following pseudo-code for getting the element with index , where 
of a linked list:
algorithm GetItemFromEnd(head, n):
// INPUT
// head = the reference to the linked list
// n = the index of the node to be fetched from the end
// OUTPUT
// Returns the data of the node at index n from the end
runner <- head
i <- 0
// Iterate until the end of the linked list
while runner != null:
if i = n:
// We finished counting to n
break
// Move runner to the next successive node
runner <- runner.next
// Increase the counter by 1
i <- i + 1
if runner = null:
Print the message 'The list is smaller than n elements'
return
// Iterate until runner points to the tail of the list
trail <- head
while runner.next != null:
runner <- runner.next
trail <- trail.next
return trail.data
5. A Walk-Through of GetItemFromEnd(head,n)
Let’s walk through the important steps of the algorithm introduced in the previous section. We take an empty pointer runner and initialize it to refer to the head node of the linked list. We now traverse through the list, moving runner to the node with index 
.
At this point, we may have already reached the end of the linked list, in which case runner = null. In such a situation, we abort and print a message to the user that the list is too small. If this is not the case, we take an empty pointer trail and set it to refer to the head node of the list.
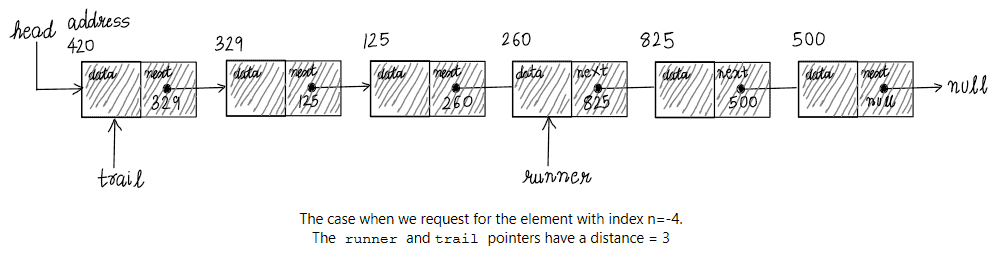
The distance between the runner and trail pointers is equal to 
. So, our setup is as follows:
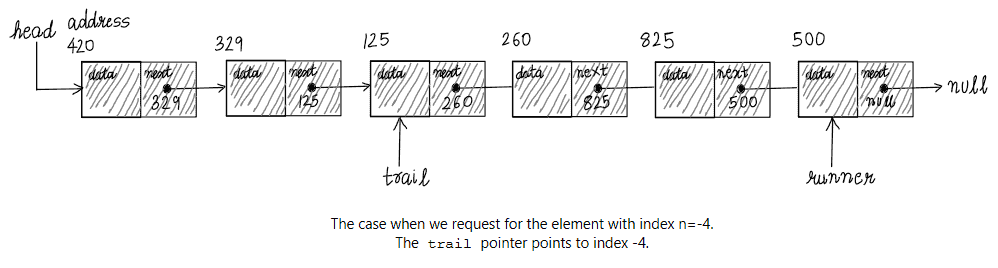
Now, we move both – the runner and the trail pointers to their respective successive nodes iteratively. Throughout these iterations, the distance between the runner and the trail is kept constant. Thus, when runner refers to the tail of the linked list, the trail pointer should point to the th node from the end of the list.
The below snap depicts the situation, when runner has reached the end of the list, for the case 
:
6. Implementation in Python
6.1. Creating the Classes
Python’s built-in list data structure is a dynamic array, offering indexed access to its elements. And so, the algorithms we have talked about so far do not apply to them; to write an implementation for the algorithms, we first need to create our own List Data Structure.
To do this, we need to use classes that are not dissimilar to classes in other languages like Scala. There are many tutorials on the internet, from comprehensive to fun.
At a minimum, we’ll need to create a Node class to store the data and a LinkedList class to maintain the state of the list:
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def append(self, data):
new_node = Node(data)
if not self.head:
self.head = new_node
return
last = self.head
while last.next:
last = last.next
last.next = new_node
With these definitions, we have set the foundation for implementing the algorithms to find the nth element from the beginning to the end of the list.
6.2. Implementing and Using GetItem Method
Python is sometimes referred to as executable pseudocode, and we can see why by implementing the GetItem algorithm almost one-to-one, with only minor differences:
class LinkedList:
# ... [previous methods]
def get_item(self, n):
runner = self.head
count = 0
while runner:
if count == n:
return runner.data
count += 1
runner = runner.next
print("Error: Index out of bounds")
return None The only appreciable difference from the pseudocode is that the head is implicit in the object, the casing difference in the name to match the naming practices of Python, and returning None when the list has fewer elements than the one we are looking for.
Using it is also very simple:
# Example usage of the refined LinkedList
ll = LinkedList()
ll.append(1)
ll.append(2)
ll.append(3)
ll.append(4)
ll.append(5)
# Try to get the 4th item (index starts at 0)
item = ll.get_item(3)
if item is not None:
print("The 3th item in the list is:", item)6.3. Implementing GetItemFromEnd Algorithm
The implementation of the method to find an element from the end is again a one-to-one translation from the pseudocode:
class LinkedList:
# ... [previous methods]
def get_item_from_end(self, n):
runner = self.head
trailer = self.head
count = 0
while count < n:
if runner is None:
print("Error: Index out of bounds")
return None
runner = runner.next
count += 1
while runner:
runner = runner.next
trailer = trailer.next
return trailer.data
And using it is as simple as with GetItem:
item = ll.get_item_from_end(3)
if item is not None:
print("The 3th item from the end of the list is:", item) 7. Conclusion
In this article, we learned about the algorithms to get an element with index of a linked list. To recap, first, retrieving an element from the beginning of the list requires initializing a current pointer to head. It should then be moved to its successor node times. Second, when retrieving an element from the end of the list, we set up two pointers runner and trail, a distance 
apart. We then move both pointers iteratively to their successor nodes until runner.next=null.