How to Rotate a Two-Dimensional Array | Baeldung on Computer Science

1. Introduction

In this topic, we’ll explain how to rotate a two-dimensional array. We’ll observe both right and left rotations.

2. Preliminary Notes

A two-dimensional array is basically a two-dimensional matrix. So, without losing any generality, we can assume our two-dimensional array is a two-dimensional matrix of elements. Let’s observe the following matrix, where each distinct element is colored differently:

It’s a $3 \times 4$ matrix. Below are the right and left rotations of the matrix by $90^{\circ}$ :

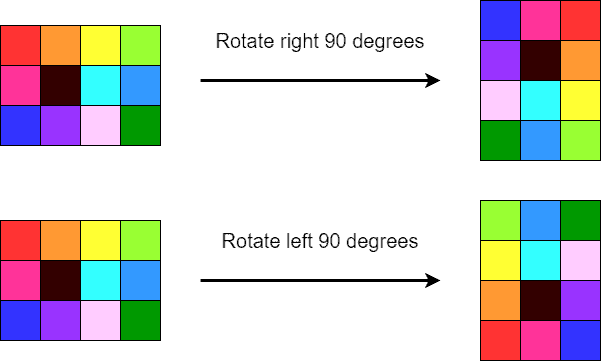
And below is the right rotation of the matrix by $180^{\circ}$ :

Note that the left rotation by $180^{\circ}$ is basically the same as the right rotation by $180^{\circ}$ .

Additionally, it’s straightforward to note that the right rotation by $\boldsymbol{270^{\circ}}$ is the same as three right rotations by $\boldsymbol{90^{\circ}}$ or one left rotation by $\boldsymbol{90^{\circ}}$ . And any $360^{\circ}$ rotation is basically no rotation. Thus, to cover all the 90-angled rotation configurations, it suffices to only observe the cases of the left and right rotations by $90^{\circ}$ and the rotation by $180^{\circ}$ .

If we put aside the optimal number of steps to perform a rotation, then the right rotation by $90^{\circ}$ is enough to reproduce all the 90-angled rotation configurations. However, that may not be optimal in the number of steps performed.

3. Custom Case: Square Matrix

First, let’s develop the rotation algorithm for a custom case when the matrix is square. To make the algorithm obvious, let’s divide our square matrix into quadrants as depicted below:

Now, the left and right rotations by $90^{\circ}$ take the form:

As we can see, we can enumerate elements in a quadrant and replace them with elements in the neighboring quadrants. The picture below illustrates the idea more precisely:

In the picture above, $n$ is the size of the matrix side. As we can see, during the right rotation by $90^{\circ}$ , the element with the position $[i][j]$ rotates to the position $[j][n - i - 1]$ , the element $[j][n - i - 1]$ rotates to the position $[n - i - 1][n - j - 1]$ , the element $[n - i - 1][n - j - 1]$ rotates to the position $[n - j - 1][i]$ , and finally, the element $[n - j - 1][i]$ rotates to the position $[i][j]$ . Shortly, there’s a four-step circular exchange happening between the appropriate elements in the matrix. Note that our indexing is zero-based.

3.1. $\boldsymbol{90^{\circ}}$ Right Rotation Algorithm

Here’s the pseudocode of the right rotation algorithm:

3.2. $\boldsymbol{90^{\circ}}$ Left Rotation Algorithm

The pseudocode of the left rotation is very similar to the right rotation, except the order of exchange is the opposite:

4. Common Case: Rectangular Matrix

The rotation algorithms described above only work for square matrices. For matrices that aren’t square, i.e., for rectangular matrices, we need to develop separate algorithms. First, let’s recall what the transpose matrix $T$ of the original matrix $M$ is. $T$ is a matrix where $i-th$ column is the $i-th$ row in $M$ .

In the example below, a $3 \times 4$ matrix is transformed into a $4 \times 3$ transpose matrix:

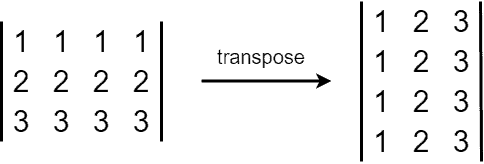
We can see that transposing partially performed the $\boldsymbol{90^{\circ}}$ right rotation task: the rows are rotated, but the column order isn’t what we need. Thus, we additionally swap the symmetric columns: for a matrix with $m$ columns, we swap columns $0$ and $m - 1$ , then $1$ and $m - 2$ , and so on. Shortly, the right rotation by $\boldsymbol{90^{\circ}}$ can be achieved by transposing followed by the symmetric column swap operation.

4.1. $\boldsymbol{90^{\circ}}$ Right Rotation Algorithm

First, let’s provide the pseudocode for transposing matrices:

Now, the pseudocode of the $90^{\circ}$ right rotation for rectangular matrices takes the form:

4.2. $\boldsymbol{90^{\circ}}$ Left Rotation Algorithm

Similarly to the right rotation, $\boldsymbol{90^{\circ}}$ left rotation is performed by transposing followed by the symmetric row swap operation. The pseudocode is below:

The algorithms of left and right rotations for rectangular matrices can be used for square matrices as well. They’ll produce correct results, though they aren’t as optimal in the number of steps as the custom algorithms for square matrices. Anyway, asymptotically, they’re the same.

4.3. $\boldsymbol{180^{\circ}}$ Rotation Algorithm

Finally, let’s provide the pseudocode for the $180^{\circ}$ rotation algorithm. The algorithm is actually optimal for any matrix so that it can be readily used for square matrices as well:

5. Complexity Analysis

All the algorithms described in this topic have $\boldsymbol{O(n * m)}$ complexity, where $\boldsymbol{n}$ is the number of rows and $\boldsymbol{m}$ is the number of columns in a matrix. In the case of square matrices, the complexity simply becomes $\boldsymbol{O(n^2)}$ .

6. Conclusion

In this topic, we’ve gone through algorithms for rotating two-dimensional matrices. First, we’ve developed optimal algorithms for square matrices, and then we’ve provided rotation algorithms for common rectangular matrices. As we’ve noted, the $\boldsymbol{90^{\circ}}$ rotation algorithms for rectangular matrices can be used for square ones as well, though the custom algorithms are better in the number of steps. The $\boldsymbol{180^{\circ}}$ rotation algorithm is optimal for any matrix.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex

1. Introduction

2. Preliminary Notes

3. Custom Case: Square Matrix

3.1. Right Rotation Algorithm

3.2. Left Rotation Algorithm