How to Reverse a Linked List

1. Introduction

In Computer Science, a linked list is a linear data structure in which a pointer in each element determines the order. In this tutorial, we’ll show how to reverse a linked list.

2. Linked List Reversal

Each element of a linked list contains a data field to store the list data and a pointer field to point to the next element in the sequence. We can use a pointer to point to the start element of a linked list:

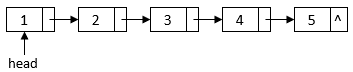
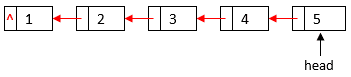
After we reverse the linked list, the will point to the last element of the original linked list, and the pointer of each element will point to the previous element of the original linked list:

3. Iterative Solution

Firstly, let’s solve a simpler version of the problem: reverse a linked list with two elements:

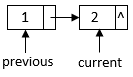
Suppose the pointer points to the second element and the pointer points to the element before the element, we can switch the link order between them with two operations:

=
=

For a linked list with more than two elements, we can traverse the linked list and use the same strategy to reverse the current element’s next pointer:

\end{tikzpicture}

algorithm reverseListIteratively(head):
    // INPUT
    //   head = The first element of a linked list
    // OUTPUT
    //   Returns the head pointer of the reversed linked list

    previous <- null
    current <- head

    while current is not null:
        nextElement <- current.next
        current.next <- previous
        previous <- current
        current <- nextElement

    return previous

In this iterative algorithm, we first set the pointer as a pointer and the as the . Then, in each iteration of the loop, we reverse the linked pointer of these two elements and shift the and pointers to the next two elements. In the end, the pointer will point to the new head element of the reversed linked list.

Since each element only has one reference to the next element, we need another pointer, ,  to store the next element before changing the pointer.

The loop traverses the whole linked list once. Therefore, the running time of the iterative algorithm is , where is the total number of elements of the linked list.

4. Recursive Solution

We can also solve the problem with a recursive solution. Let’s first consider a simpler case where we have reversed the rest of the linked list after the element:

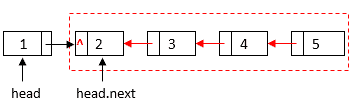
We only need to reverse two elements: and . At the beginning, the pointer of the is . We should change that to make it point to . Then, we need to change the next pointer of element to to finish the reversal:

=
=

We can extend this solution to a recursive algorithm of reversing a linked list staring with a element. Firstly, we can reverse the linked list starting with element by recursively calling our reversal function.  Then, the linked list becomes our simpler case. Therefore, we can reverse the last two elements, and , with the above two operations.

We can construct a recursive algorithm based on this approach:

algorithm reverseListRecursively(head):
    // INPUT
    //   head = The first element of a linked list
    // OUTPUT
    //   Returns the head pointer of the reversed linked list

    if head is null:
        return null

    if head.next is null:
        return head

    node <- reverseListRecursively(head.next)
    head.next.next <- head
    head.next <- null

    return node

In this recursive algorithm, we first check base cases where the input pointer is or points to a single element. Then, we recursively call the function on the element to reverse the rest of the linked list. Finally, we reverse and elements to finish the reversal.

The recursive algorithm also traverses the whole linked list once. Therefore, the running time is , where is the total number of elements of the linked list.

5. Conclusion

In this tutorial, we showed a sample linked list and its reversal. Also, we discussed two algorithms that can reverse a linked list in linear time.