Patience Sort Algorithm | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll discuss one of the efficient sort algorithms – patience sort. Its creation is motivated by a simple variant of the patience card game or, as it’s also called, solitaire.

2. A Simple Variant of the Patience Game

There’s a deck of cards, which are pulled out one by one from the deck and put into piles. Then, the pulled-out card is placed on top of one of the piles. The game continues until the deck is empty.

We must follow two rules when placing cards into piles:

We are only allowed to place the pulled-out card into a pile if the pulled-out card is less or equal to the pile’s top element
When there’re no piles to put the current card into, form a new pile and put it into it

The objective of the game is to form as few piles as possible.

We’ll use a sequence of numbers instead of cards to review an example. Suppose we have a sequence of numbers $S = [5, 7, 5, 9, 1, 2, 5, 8, 3, 11, 6, 4]$ . Let’s play the game described above with the sequence. Initially, we have the sequence as a deck and no piles:

We pull out the first value, which is 5, and create the first pile:

The next value, 7, can’t be placed into the first pile as 7 > 5, creating a new pile. Next, we pull out the third value, which is 5 again, and we may put it into both piles. Let’s put it into the first pile. Additionally, we pull out 9, which creates the third pile:

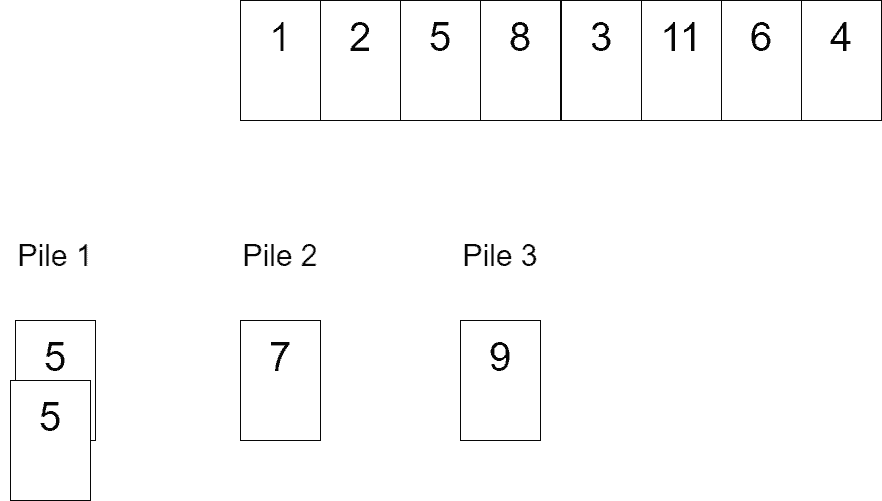
Next, we pull out the next three values, which are 1, 2, and 5. We may put 1 into any pile; we select the second pile. Next, 2 may be put into the first or the third piles; we select the first one. Finally, after placing 1 and 2, 5 may only be placed into the third pile:

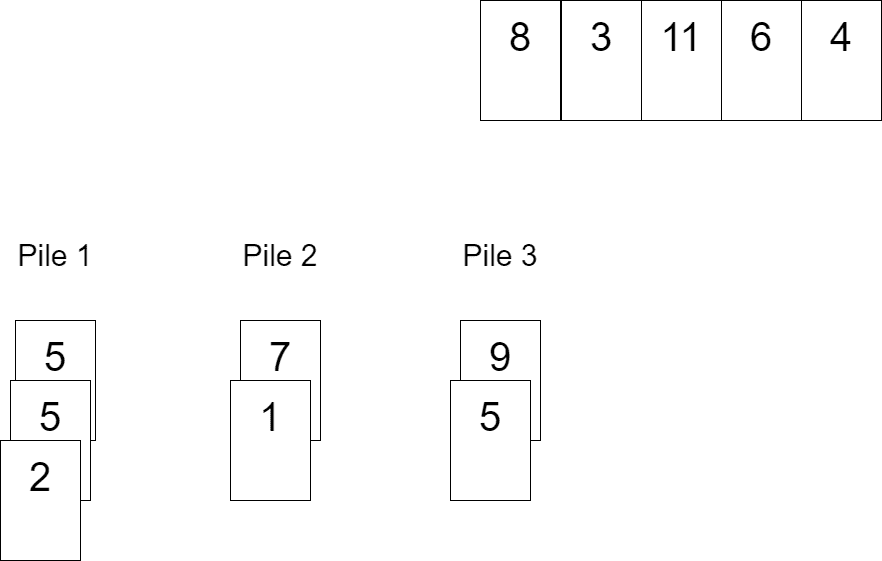
Let’s pull 8 and 3. 8 forms the fourth pile. Meanwhile, 3 may be put into either the third or the fourth pile. Let’s put it into the fourth pile:

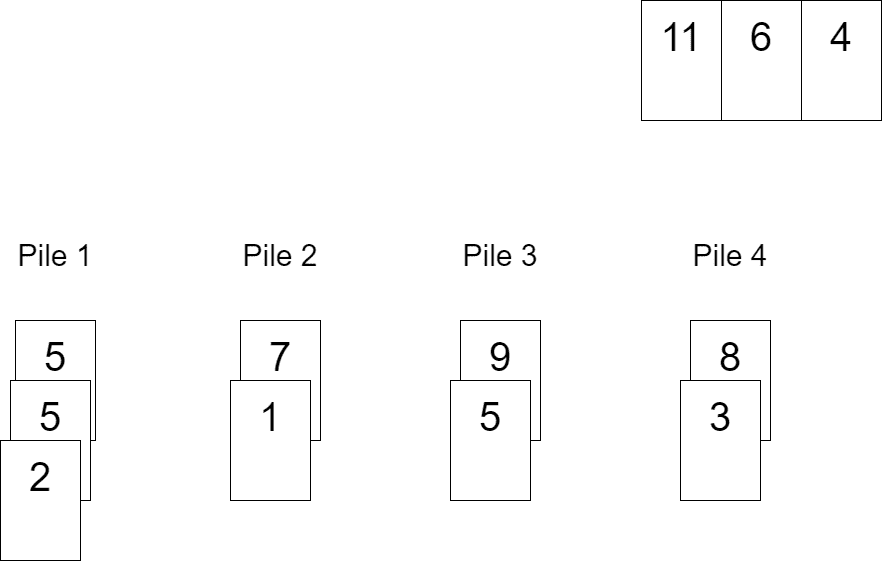
Finally, we pull out the remaining three values – 11, 6, and 4. 11 forms the fifth pile, 6 is placed into the fifth pile, and we select 4 to be put into the third pile:

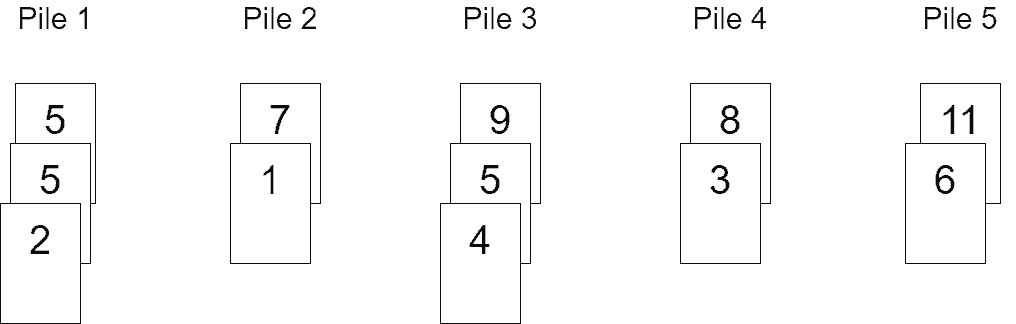
We’re done now. We observe that each pile is a sequence of values sorted in ascending order. Note that we’ve played the game according to its rules, but we haven’t paid attention to the objective yet – getting as few piles as possible. That will be discussed next.

3. Algorithm Description

Patience sort is an unstable sorting algorithm that consists of two parts: distributing the elements into the sorted piles and merging the sorted piles to get a single sorted sequence. Let’s discuss each phase in detail. In our discussion, $N$ is the number of elements, and $K$ is the number of piles.

3.1. Phase 1: Distribute the Elements into Piles

In the previous section, we distributed a sequence of values among several sorted piles. We simply picked a matching pile and placed the pulled-out value into it. Algorithmically, we need to iterate over the piles until we meet a matching pile. Obviously, that takes $\boldsymbol{O(N)}$ time to locate such a pile. There’re $\boldsymbol{N}$ elements, so overall, the phase of the element distribution takes $\boldsymbol{O(N^2)}$ . That’s slow; we want a linearithmic algorithm.

Note that we haven’t yet addressed the game’s objective – getting as few piles as possible. This is one of the problems that may be solved using the greedy approach. Instead of placing the pulled-out value on any matching pile, we’ll place it on the leftmost matching pile. By following the greedy approach, we get as few piles as possible. Additionally, the top elements of the piles form a sorted sequence, i.e., if we go over the top elements of the piles from left to right, we’ll get a sorted sequence. That’s good because now we can enable the binary search instead of the linear scan to find the appropriate pile.

Overall, this phase runs in $\boldsymbol{O(N * log(K))}$ . Let’s also display what piles we get if we follow the greedy approach:

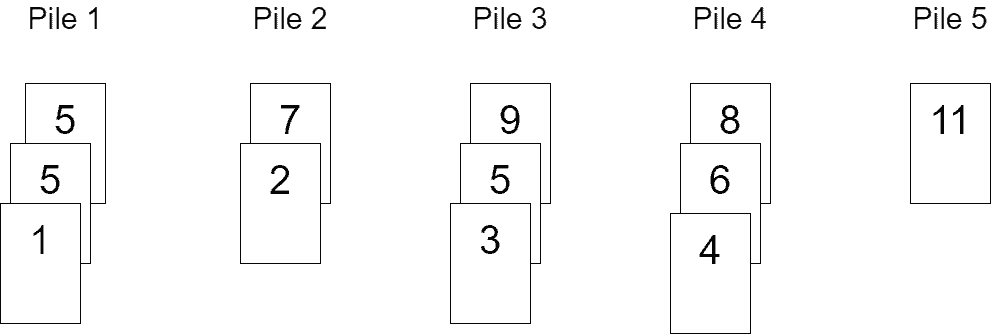
Note that the number of piles is five as before, so this is the optimal count for piles, and there’s no way to get fewer piles.

3.2. Phase 2: Merge the Sorted Piles into a Single Sorted Sequence

We know how to merge $K$ sorted sequences into a single sorted sequence using one of the K-way merge algorithms in $\boldsymbol{O(N * log(K))}$ time. That can be done using, for example, the MinHeap data structure consisting of the current top elements of the piles. Each element in the MinHeap points to its pile, so when it’s removed from the MinHeap as the current minimum, the next value of the pile has a chance to be inserted into the MinHeap.

Let’s create the MinHeap for the output of the first phase constructed above:

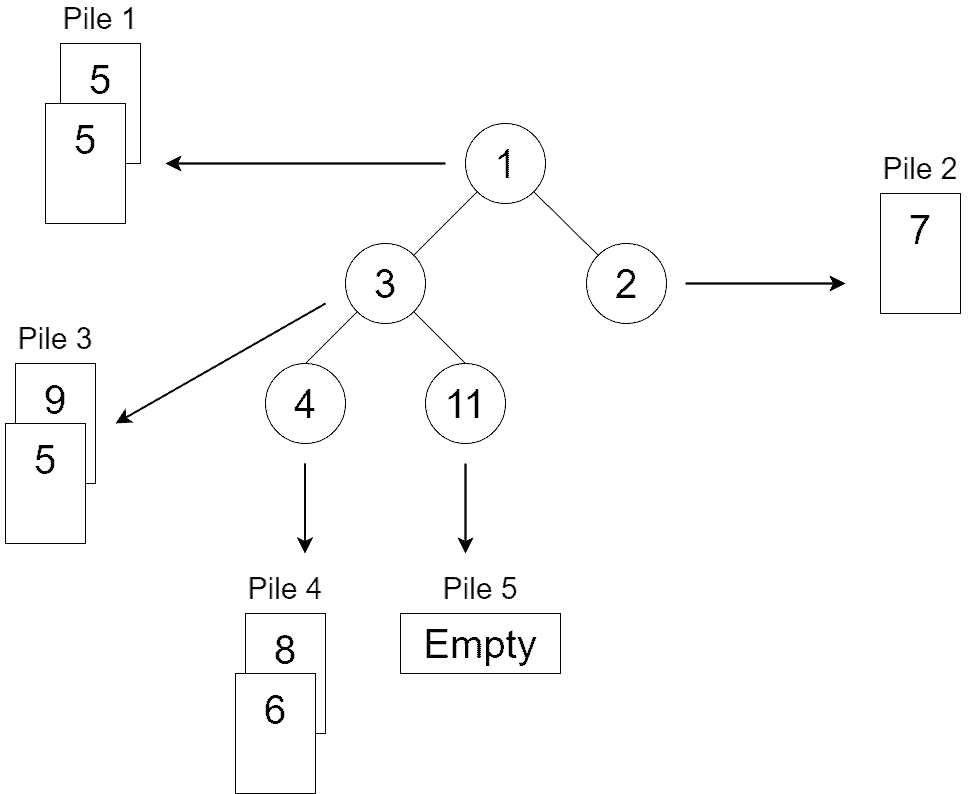
After running the procedure of the minimum extraction and replacing it with the next element in the minimum’s pile $N$ times, we get a single sorted sequence of elements in the output: $S = [1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 9, 11]$ .

4. Algorithm Pseudocode

After understanding all the details of the patience sort, we’re able to write its pseudocode. We assume that $input$ and $output$ are 1-indexed arrays of elements. We also assume there’s a function $\textnormal{BINARYSEARCH(\textit{piles, element})}$ which accepts an array of piles and an element and returns the index of the leftmost pile that $element$ may be placed into. If no such pile exists, the function returns -1:

The pseudocode above implements all the steps of patience sort we’ve discussed.

5. The Complexity Analysis

As we’ve discussed earlier, the patience sort algorithm consists of two phases, and each phase runs in $O(N * log(K))$ time. Thus, the algorithm itself runs in $\boldsymbol{O(N * log(K))}$ time.

The space complexity is $\boldsymbol{O(N)}$ as we need to maintain the piles and their contents.

6. Conclusion

In this topic, we’ve discussed the patience sort algorithm. It’s a linearithmic sort algorithm consisting of two phases: distributing the elements into sorted piles, and merging the sorted piles into a single sorted sequence.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex