Optimization: Gradient-Based Algorithms | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll talk about gradient-based algorithms in optimization. First, we’ll make an introduction to the field of optimization. Then, we’ll define the derivative of a function and the most common gradient-based algorithm, gradient descent. Finally, we’ll also extend the algorithm to multiple input optimization.

2. Introduction to Optimization

The goal of an optimization algorithm is to find the input value $\mathbf{x}$ that minimizes or maximizes the output value of a function $\mathbf{f(x)}$ .

We usually work only with minimization algorithms since a maximization problem of $f(x)$ can be transformed into a minimization problem of $-f(x)$ . So, from now on, we’ll talk only about minimization problems.

Formally, we usually refer to the function $\mathbf{f(x)}$ that we want to minimize as an objective function or loss function.

An example of a simple minimization problem is the Linear Least Squares, where we want to approximate a linear function given some sample data. In this case, the objective function is defined as:

$f(x) = \frac{1}{2} || A \ x - b ||^2$

Moreover, we have the minimum value denoted as:

$x^{\ast} = argmin \ f(x)$

3. Derivative of a Function

An essential part of every gradient-based algorithm is the gradient, as the name suggests. First, we’ll focus on the case of a single input $x$ where the gradient of a function $f(x)$ is defined as the derivative $f'(x)$ or $\frac{df}{dx}$ .

Geometrically, the derivative of a function at point $x$ corresponds to the function’s slope at this point. This concept is illustrated in the below diagram:

To put it more simply, the gradient specifies how a small change in input will affect the output.

4. Gradient Descent

Gradient descent is a very famous gradient-based algorithm first proposed by Augustin-Louis Cauchy.

It is based on a very simple observation:

The value of $f (x - \epsilon \ sign (f^{'}(x) )$ is less than $f(x)$ for small changes in $\epsilon$ . So, we can reduce the value of an objective function $\mathbf{f(x)}$ by changing the input $\mathbf{x}$ to the opposite sign of the computed derivative.

Now, let’s present an example to illustrate better how gradient descent works. We suppose that we want to minimize the function:

$f(x) = \frac{1}{2} x^2$

with derivative

$f^{'}(x) = \frac{1}{2} 2 x = x$

We aim to find the global minimum of $f(x)$ that holds when $x=0$ . So, we start at a random input value of $x_1$ :

$x_1 > 0$ it means that $f^{'}(x_1) > 0$ and we can decrease the value of $f$ be moving leftward. This is equivalent to reducing the value of $x_1$ by a value $\epsilon$
$x_1 < 0$ it means that $f^{'}(x_1) < 0$ and we can decrease the value of $f$ be moving rightward. This is equivalent to increasing the value of $x_1$ by a value $\epsilon$

The diagram below shows the whole procedure:

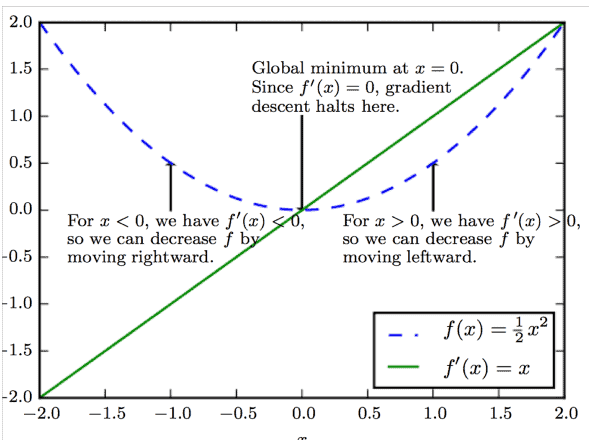
We stop the procedure when after some iterations, the change in the value of $f(x)$ will be less than a predefined small threshold, meaning we have reached the minimum of the function.

5. Optimizing With Multiple Inputs

In case of multiple inputs ( $x_1, x_2, ..., x_n$ ), we have to use partial derivatives $\frac{\partial f}{\partial x_i}$ that measures how the function $f(x_1, x_2, ..., x_n)$ changes as only one of its inputs $x_i$ changes. In this case, the gradient is a vector that contains the partial derivatives of the function and is denoted as $\nabla_x f(x)$ .

Suppose we generalize the method of gradient descent that we mentioned for the case of multiple inputs. In that case, we observe that the positive gradient points directly uphill, and the negative gradient points directly downhill. So, we can decrease the value of $\mathbf{f(x)}$ by moving in the direction of the negative gradient.

6. Conclusion

In this article, we talked about gradient-based algorithms in optimization. First, we introduced the important field of optimization and talked about a function’s derivative. Then, we presented the gradient descent algorithm, which is the most common gradient-based algorithm. Finally, we generalized the algorithm for the case of multiple inputs.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex