Looping in a Spiral

1. Overview

In this tutorial, we’ll study an algorithm for traversing the elements of a matrix in a square spiral.

2. What Is a Spiral?

A spiral is a curve that originates from a point called the center and progressively gets farther as it winds around it. In a polar plane, a spiral has the form of a continuous monotonic function that relates the angle to the radius , as . This is the graph of one of the most common spirals, the spiral of Archimedes:

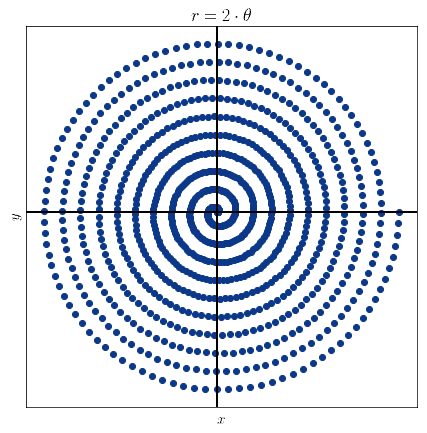
Generalized algorithms for computing spirals that extend over surfaces with arbitrary shapes also exist. For looping over matrices, however, a slightly different definition is needed.

3. Spirals and Matrices

In relation to matrices, the spiral that loops over its elements is called a square spiral. A square spiral has this shape:

Because we can’t define it as a continuous function, we can instead define it procedurally. It’s intuitive to understand how it functions, if we imagine traversing a matrix in a spiral fashion starting from one of its elements. Let’s use this sample matrix:

We can indicate with numbers the order in which the elements have to be traversed, starting from 1, to produce a square spiral. Traversing the matrix in spiral then corresponds to vectorizing it by starting from one corner and looping over all elements, and then terminating in the center:

Or, alternatively, by starting from the center and then terminating in one of the corners:

The traversal occurs by moving in one direction by steps, then rotating, then moving more steps, then rotating, then incrementing the counter and repeating. Notice also how the traversal from the center to the corner is simply a reversal of the traversal, and that this is valid for both clockwise and counter-clockwise spirals.

4. Non-Square Matrix

If the matrix is non-square, and has rows and columns, such that , then we’ll need some extra steps. We’ll first extend it to the square matrix of size , and then skip all elements that are present in the square but not in the rectangular matrix:

We’re now going to study the algorithm that performs this traversal. One last note before that: instead of using rows and columns as a coordinate system, it’s more practical to shift the origin to the center of the matrix. This means that, if and are odd, we place the origin to :

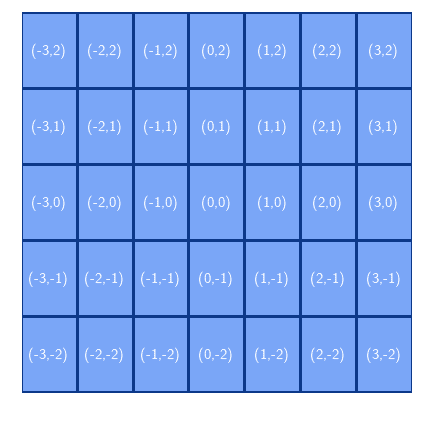
4. Traversing From Center to Corner

We can now study an algorithm that traverses the matrix from the origin , up to the corner , in a square spiral. To build one, we need to define two pointers that store the coordinates of the current element relative to the center, and two direction vectors . The algorithm is this:

algorithm ClockwiseSquareSpiral(N, M, A):
    // INPUT
    //    N = the number of rows in the matrix
    //    M = the number of columns in the matrix
    //    A = the matrix to traverse
    // OUTPUT
    //    Traverses the matrix A from the center to the corner in a clockwise spiral
    
    x <- 0
    y <- 0
    dx <- 0
    dy <- -1
    
    for i <- 0 to (max(N, M))^2:
        if -N/2 < x <= N/2 and -M/2 < y <= M/2:
            a[x, y] is in A, so we do something with it
        if x = y or (x = -y and x < 0) or (x = 1 - y and x > 0):
            // End of current segment, rotate direction
            temp <- dx
            dx <- -dy
            dy <- temp
        x <- x + dx
        y <- y + dy

When executed on a 3 by 5 matrix, as in the example above, the algorithm produces the traversal in the expected order:

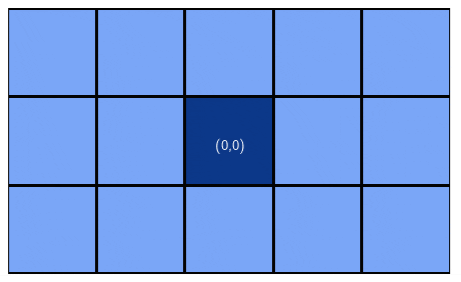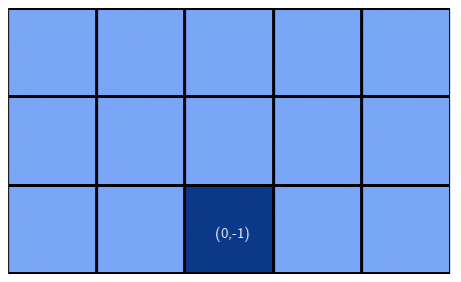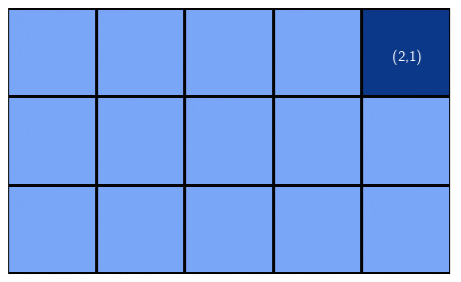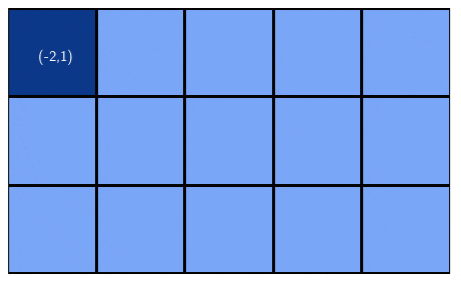
We can also define a counter-clockwise rotation, by simply modifying slightly the second if statement:

algorithm CounterClockwiseSquareSpiral(N, M, A):
    // INPUT
    //    N = the number of rows in the matrix
    //    M = the number of columns in the matrix
    //    A = the matrix to traverse
    // OUTPUT
    //    Traverses the matrix A from the center to the corner in a counter-clockwise spiral
    
    x <- 0
    y <- 0
    dx <- 0
    dy <- 1
    
    for i <- 0 to (max(N, M))^2:
        if -N/2 < x <= N/2 and -M/2 < y <= M/2: 
            // a[x, y] is in A, so we do something with it
        if (x = -y) or (x = y and x > 0) or (x = -1 + y and x < 0):
            // End of current segment, rotate direction
            temp <- dx
            dx <- dy
            dy <- -temp
        x <- x + dx
        y <- y + dy

And as expected, this is the output with a 3 by 7 matrix:

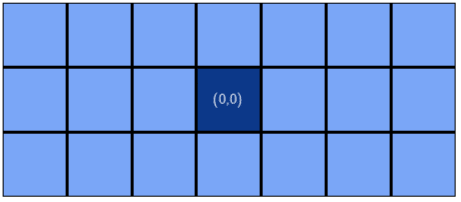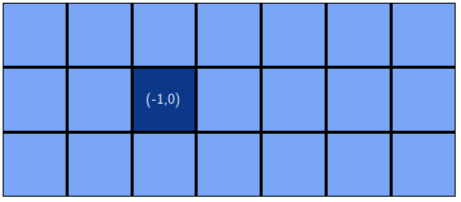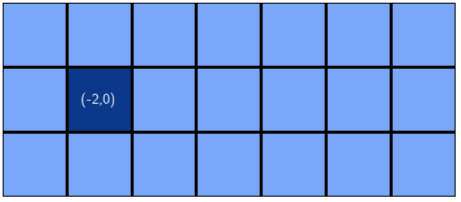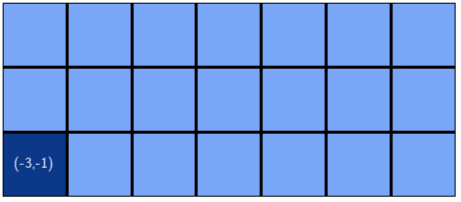
5. Traversing from Corner to Center

If we want instead to traverse the matrix from a corner to the center, we can refer to the consideration we made above. All that we need to do is to store in a list the order of traversal and then reverse it.

For example, this is the reverse spiral traversal of a 5 by 7 matrix:

6. Conclusion

In this article, we studied how to loop over the elements of a matrix in a square spiral pattern.