Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll discuss two different types of search algorithms: hash lookup and binary search. We’ll present a time complexity comparison between these two search techniques.
Hash lookup is used in the hash table data structure. We use the hash data structure to map keys and values in an unsorted way. Additionally, a key means a unique identifier that points to the values we’re storing. A hash table is also known as the hash map.
Before talking about hash lookup, let’s explore the hashing technique. It’s a method of mapping the keys and values in the hash table using a hash function. We can map given keys of arbitrary size to fixed-size values using a hash function. The fixed-size output returned by a hash function is known as the hash value. We store hash values in a fixed-size table called a hash table. This whole process is called hashing.
Hash lookup is the process of searching a key from the hash table. Let’s understand hash lookup with an example. Suppose we want to order food online from a restaurant. While ordering food, we need to enter certain information, including phone number, address, and payment details. Therefore, the easy way for the restaurant to keep track of the food orders is to store the orders with either a phone number or the serial number. Hence, a user can either enter a phone or a serial number in the system to check the status of the placed food order.
Hence, to make the search easy, the restaurant can maintain a logbook, in which the phone numbers corresponding to the food orders are stored. However, there’re some issues with this approach. First of all, the restaurant wastes a lot of space storing the phone number as an index. Depending on the country, a phone number can contain 10 digits.
Secondly, there’s a probability of duplicate entries and vacant indices. It can result in slowing down the search and information retrieval process:

Therefore, to overcome this issue, we need to reduce the size of the index. Additionally, we must ensure that the table is redundant-free. One possible approach is to divide all phone numbers with a fixed number and use the quotient as the index.
Therefore, the restaurant could use the phone number to get the status of the food orders and successfully reduce the size of the table. Instead of storing long digit phone numbers as a key, we’re storing single-digit numbers. For example, for order number 3, the user enters the phone number. We retrieve the order status from the index 7 in the log table:
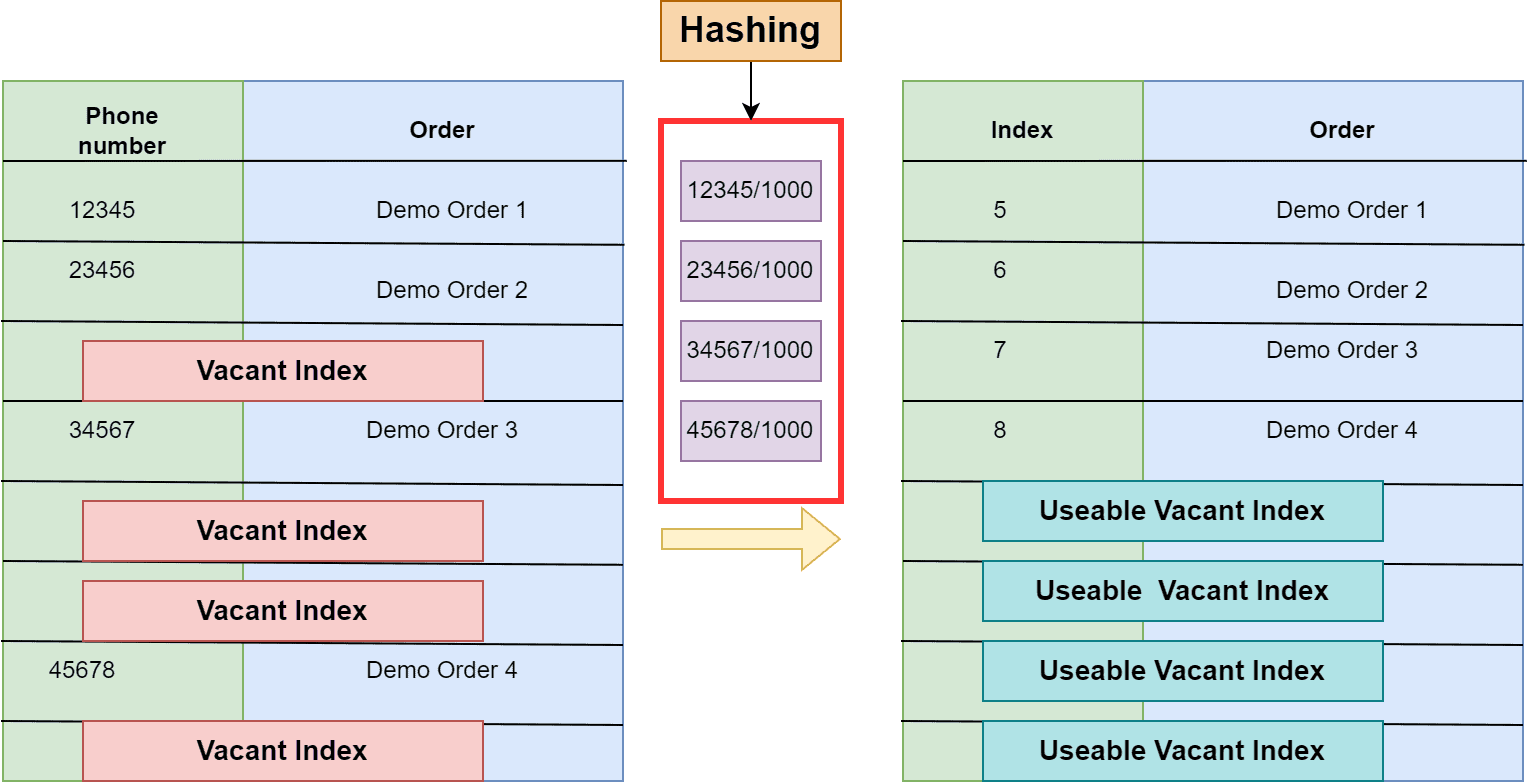
It’s an exact example of hashing. Here, we use the phone number as a key. Additionally, we calculate the indices of the table using a simple hash function. The logbook is a hash table. In this example, it’s just a coincidence that phone numbers are sorted in increasing order, but it’s not a necessary condition in the hash table data structure:
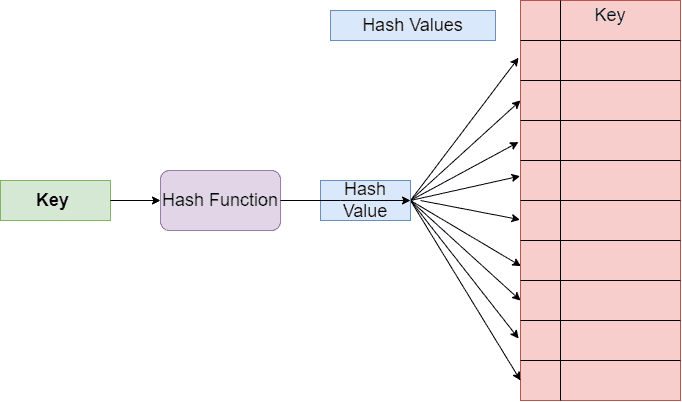
In the hash table data structure, it’s essential to use a good hash function. For example, the simple hash function we used is limited to 10 output indices. Hence, we might get the same hash value for multiple keys (phone numbers). Therefore, in order to avoid collisions, separate chaining is one of the most popularly used.
General operations in the hash table data structure such as search, insertion, and deletion take in best as well as in the average cases. In the worst case, it can take
. Complexity in the hash table also depends upon the hash function. A complex hash function can take significantly more time than a simple one. Let’s discuss the best, average and best case time complexity for hash lookup (search) operation in more detail.
In the best case, when we search for an element in the hash table, we directly find the element at the location of the hash value index. Therefore, we need to calculate the hash value using a simple hash function and retrieve the element from the hash table. Thus, in the best case, the time complexity of the hash lookup operation is .
When the hash function is appropriately defined, the number of collisions is less. Additionally, when the number of input entries is large, the hash table contains chaining. The average case occurs when the length of all the chains is the same. In this case, in order to calculate the hash value from the given input key takes time. Additionally, finding the location of the element in the hash table takes
time. Therefore, in the average case, the hash lookup operation takes
time in total.
The worst-case can occur when the hash table is full. Therefore, in order to search for an element, we need to traverse the whole hash table. In this case, the hash table is equipped with chaining a single list containing all the elements. Hence, we need to traverse all the elements in that specific list in order to retrieve the required element. Therefore, if there’re elements in the table, the hash lookup operation takes
times.
Binary search is widely used and one of the fastest search algorithms. It works based on the divide and search principle. The data set must be sorted in increasing or decreasing order before providing it as input to the binary search algorithm. In this algorithm, we first compare the target value with the middle value of the sorted array.
If the target value is less than the middle value, we leave half of the array without any search operation. We only search in the part of the array where the value of the elements is greater than the target value. Similarly, we continue the search operation and divide the remaining half of the array into two parts. Again we compare the target value and the value of the middle element. We continue in such a manner until the target element is found.
Let’s take the previous example of the restaurant and suppose the attendant is using the binary search algorithm to find the details of the orders using a phone number as a key. Therefore, the first step is to store all phone numbers in either increasing or decreasing order. Let’s suppose we store them in increasing order:

Now when the attendant wants to search for details of any orders, firstly, he opens the logbook and compares the middle phone number with the target phone number. Depending upon the comparison, the search proceeds further. Let’s take an example. We want to search the phone number 12345 from the logbook using binary search:
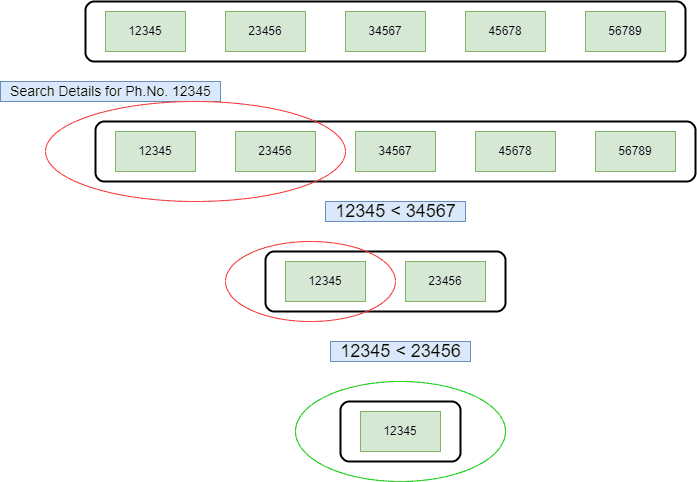
Hence, as we can see, the value of the middle element is 34567, which is greater than the target value. Therefore, we won’t search for the elements greater than the middle element’s value. Moving forward with our search, in the next step, we compare with the middle element. As the value of the middle element is greater than the target value, we look for the elements on the left of the middle element.
Let’s talk about the time complexity of the binary search method. When the target value is the middle element in an array, we can find the desired element in the very first iteration. Therefore, in the best case, the time complexity of the binary search would be .
Let’s assume the given array contains distinct elements. In an average case scenario, the target value can be found in any index from
to
. Additionally, it may happen that the target value is not present in the given array. Therefore, in the average case, the time complexity of the binary search is
.
In the worst case, the target element is either in the first or last index of the given array. The search algorithm needs to search half of the given array in such a case. Therefore, in the worst case, the time complexity of the binary search operation would be .
We discussed the different case scenarios and associated time complexities for hash lookup and binary search. Let’s summarize the time complexity discussion and present it in a table:
| Hash Lookup | Binary Search | |
|---|---|---|
| Best Case Time Complexity} | ||
| Average Case Time Complexity | ||
| Worst Case Time Complexity |
Hence, as we can see in the table, both the methods take the same time in the best case. Therefore, the performance is the same. However, in the average case scenario, hash lookup is significantly faster than binary search. In real applications, we mainly consider an average case scenario in order to test and compare the performance of different methods. Therefore, hash lookup is a better choice in such cases.
However, binary search outperforms the hash lookup method in the worst case. Therefore, the choice between binary search and hash lookup is dependent on the application and scenarios.
Additionally, searching for any element in the hash table depends upon the size of the element. The time complexity for searching in the hash table depends on the hash function. The hash function is less costly. However, a complex hash function can impact the performance.
On the other side, in order to use binary search, it’s mandatory to provide a sorted array as an input. The binary search can’t be performed on an unsorted array. Unlike binary search, hash lookup can work on sorted and unsorted arrays.
In this tutorial, we discussed two searching methods: binary search and hash lookup. We explained the basics of both methods using examples. Finally, we provided a time performance comparison between both methods.