Error Detection: Hamming Code | Baeldung on Computer Science

1. Introduction

Error detection and correction are crucial to ensure reliable data transmission between devices. One of the most widely used error detection and correction methods is Hamming code. Richard Hamming developed it in 1950 at Bell Labs. In particular, it can detect and correct a single-bit error by adding redundant (or parity) bits to the original data.

A few use cases of Hamming code include:

- Computer memory systems: RAM and hard disk
- Communication networks: Bluetooth, ethernet, and wi-fi
- Digital signal processing: Satellite communications and digital audio broadcasting

In this tutorial, we’ll first study the basic terms of Hamming code, such as redundant bits, parity bits, and parity bit calculation. Next, we’ll provide an illustrative example of how to encode a data block using the Hamming code. Then, we’ll explore the various steps involved in error detection and correction. After that, we’ll discuss the advantages and limitations of the Hamming code. Finally, we’ll wrap up the tutorial with a brief summary of the topics covered.

2. Hamming Code Basics

In this section, we’ll discuss the fundamental terminologies of the Hamming code, including redundant bits, parity bits, and parity bit calculation.

2.1. Redundant Bits

The central idea of the Hamming code is based on redundancy. In general, the sender first divides the original data into fixed-sized blocks. It then adds some extra redundant bits to each data block before transmitting the block to the receiver. Upon reception, the receiver uses these bits to detect transmission error, locate the corrupted bit, and correct it. We can calculate the required number of redundant bits using the equation:

$2^R \geq M + R + 1$

In this equation, $R$ is the number of redundant bits, and $M$ is the number of data bits in a block.

2.2. Parity Bits

We add parity bits as redundant bits to an original data block for detecting and correcting errors during transmission. These bits ensure that each data block’s total count of $1$ is either even or odd. There are two types of parity bits:

Odd parity bit: We set a parity bit to $1$ when the count of $1$ in a bit sequence is even; otherwise, we configure it to $0$ .

Even parity bit: We fix a parity bit to $1$ if the count of $1$ in a given set of bits is odd; otherwise, we set it to $0$ .

2.3. Parity Bit Calculation

A Hamming code has $N$ number of bits, which is the sum of $M$ data bits and $R$ parity bits. We now discuss the step-by-step process to obtain the position and value of parity bits:

At first, we compute the number of parity bits $R$ using $2^R \geq M + R + 1$ and the total number of bits $N$ in the Hamming code using $N = M + R$
Next, we convert the bit positions from $1$ to $N$ into binary numbers, i.e., $[0001,0010,0011,0100, 0101, 0110, 0111,1000,\cdots]$
Then, we label the bit positions corresponding to the power of $2$ as parity bits and the remaining positions as the data bits, e.g., $[P_1,P_2,D_1,P_3, D_2, D_3, D_4,P_4,\cdots]$
At last, we determine the value of each parity bit in the Hamming code iteratively. In each iteration, we determine the value of parity bit $P_i$ by counting the number of $1$ in the bit positions that have $1$ in the $i^{th}$ position from the least significant bit in their binary representations. Then, we set the parity bit $P_i$ to $1$ if the number of $1$ is odd, considering even parity; otherwise, we set it to $0$

3. An Illustrative Example

Let’s break down the process of generating a Hamming code by looking at an example binary data block $\boldsymbol{10110110001}$ . This will help us understand how the Hamming code works and how it detects and corrects errors during data transmission. We’ll now apply each of the steps discussed in the previous section, one by one.

Step 1: The number of parity bits is $R = 4$ since $M = 11$ and $2^4 \geq 11 + 4 + 1$ . Therefore, the length of the Hamming code is $N = 11 + 4$ , that is, $N = 15$ .

Step 2: The binary conversion of the bit positions from $1$ to $15$ is $[0001,0010,0011,0100, 0101, 0110, 0111,1000,1001,1010,1011,1100,1101,1110,1111]$ .

Step 3: The parity bits are placed at the positions $[1,2,4,8]$ since they are power of $2$ . In contrast, the data bits are kept at the positions $[3,5,6,7,9,10,11,12,13,14,15]$ . The image below shows the labeling of parity and data bits:

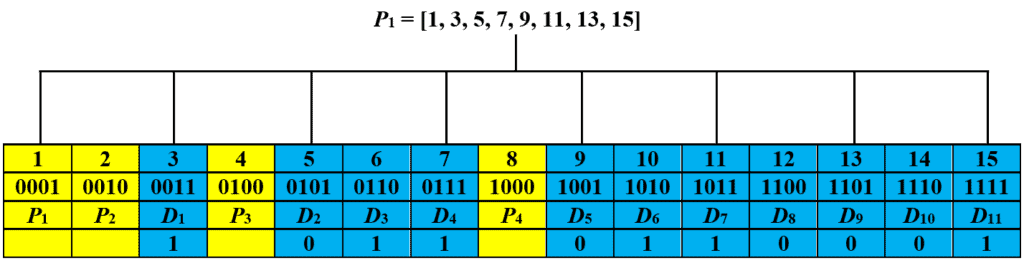
Step 4 – iteration 1: In the first iteration, we calculate the value of parity bit $P_1$ by counting the number of $1$ at the positions $[1,3,5,7,9,11,13,15]$ . These positions are chosen because their first bit from the least significant bit is equal to 1 in their binary representations. It is illustrated by:

We consider even parity and set the parity bit $P_1 = 0$ since the count of $1$ at the positions $[1,3,5,7,9,11,13,15]$ is $4$ . The updated code is:

Step 4 – iteration 2: Next, the value of parity bit $P_2$ is calculated based on the number of $1$ at the positions $[2, 3, 6, 7, 10, 11, 14, 15]$ . This is because the second bit from the least significant bit of these positions are 1 in their binary representations:

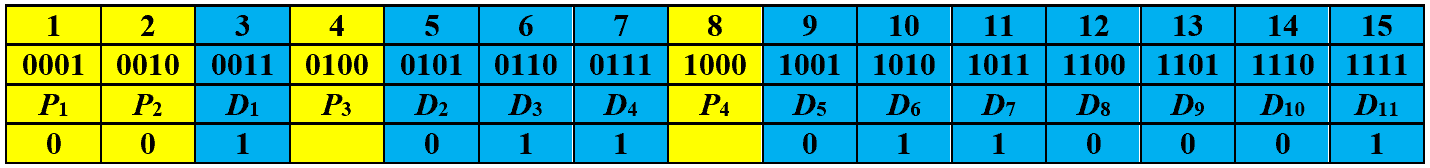
We then assign $P_2 = 0$ because there are $6$ occurrences of $1$ at the positions $[2, 3, 6, 7, 10, 11, 14, 15]$ . The new code is:

Step 4 – iteration 3: In the third iteration, we calculate the value of parity bit $P_3$ . To do so, we first count the number of $1$ at the positions $[4, 5, 6, 7, 12, 13, 14, 15]$ . The reason is that the third bit from the least significant bit in the binary representation of these positions is $1$ . It can be seen in the image below.

Next, we set the value of parity bit $P_3=1$ because we count $3$ instances of $1$ at the positions $[4, 5, 6, 7, 12, 13, 14, 15]$ . Now, the code is:

Step 4 – iteration 4: We finally count the number of $1$ at the positions $[8,9,10,11,12,13,14,15]$ to finalize the value of parity bit $P_4$ . This is because the fourth bit from the least significant bit is equal to 1 in the binary representation of these positions:

Hence, we set the parity bit $P_4 = 1$ since the count of $1$ at the positions $[8,9,10,11,12,13,14,15]$ is $3$ . The final Hamming code is:

4. Error Detection and Correction

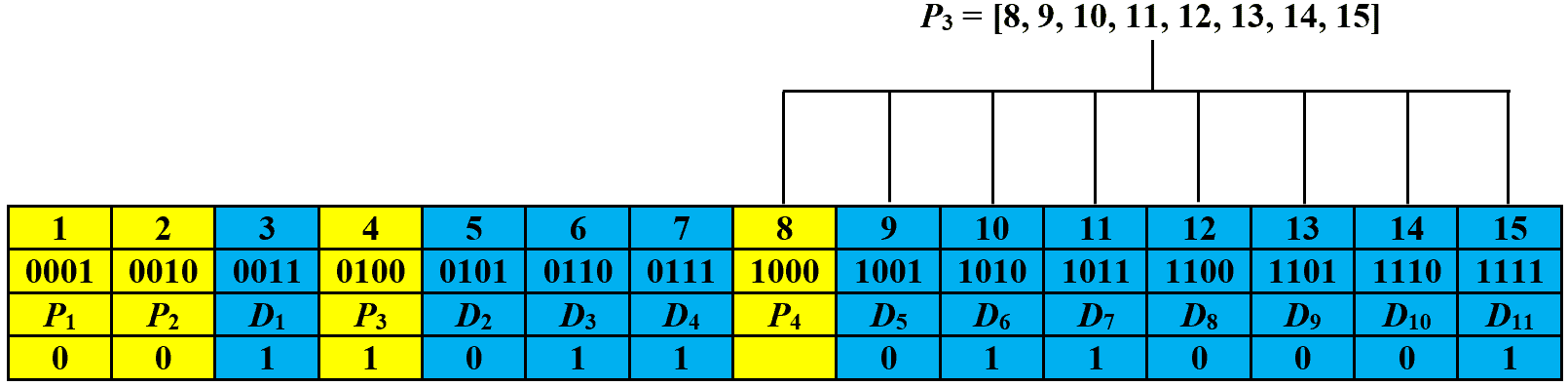
Let’s first discuss how to detect if there is an error in the received code. To do so, we recalculate the values of parity bits and perform parity checks. In particular, we record a $1$ for a parity check if the assigned and observed parity bits do not match. Otherwise, we record a $0$ . The recorded values are then written from right to left to form the checking number. The code is error-free if the checking number is zero. Otherwise, an error has occurred at the bit position corresponding to the checking number, given that there is only a single-bit error.

Let’s assume that the eleventh bit of the codeword generated in the previous section is changed from $1$ to $0$ during transmission. Then, the received code is:

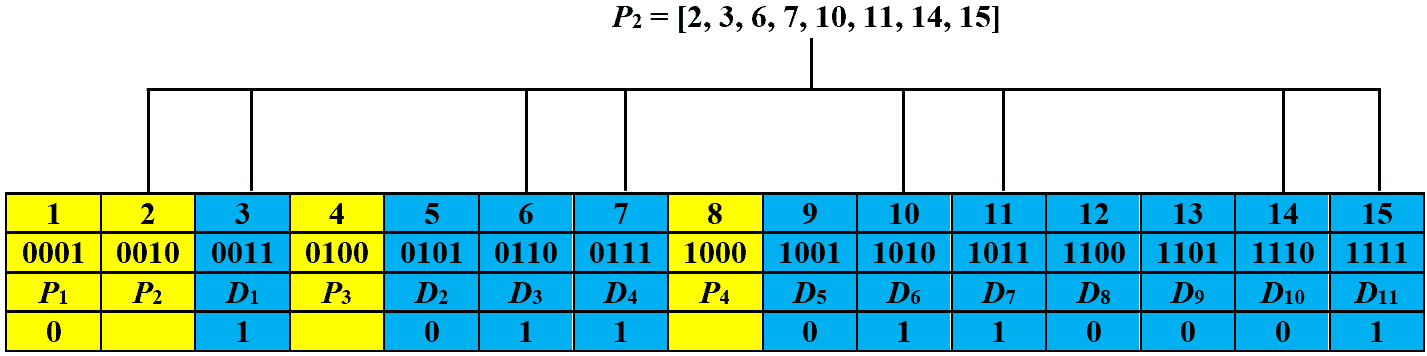
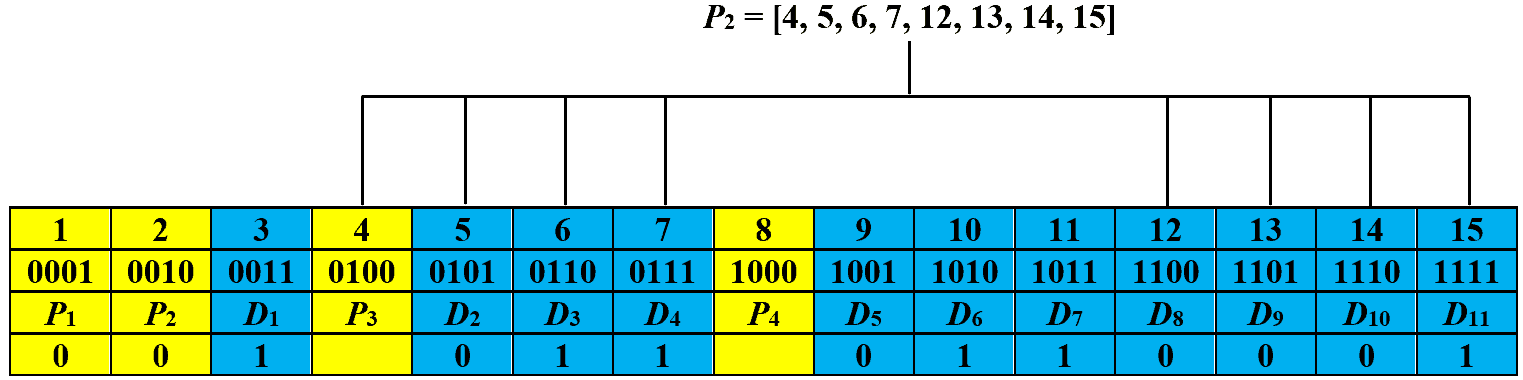
Now, we recalculate the parity bits and record their values based on the assigned and observed parity bits. The images below show the recorded values for parity bits $P_1$ , $P_2$ , $P_3$ , and $P_4$ , respectively:

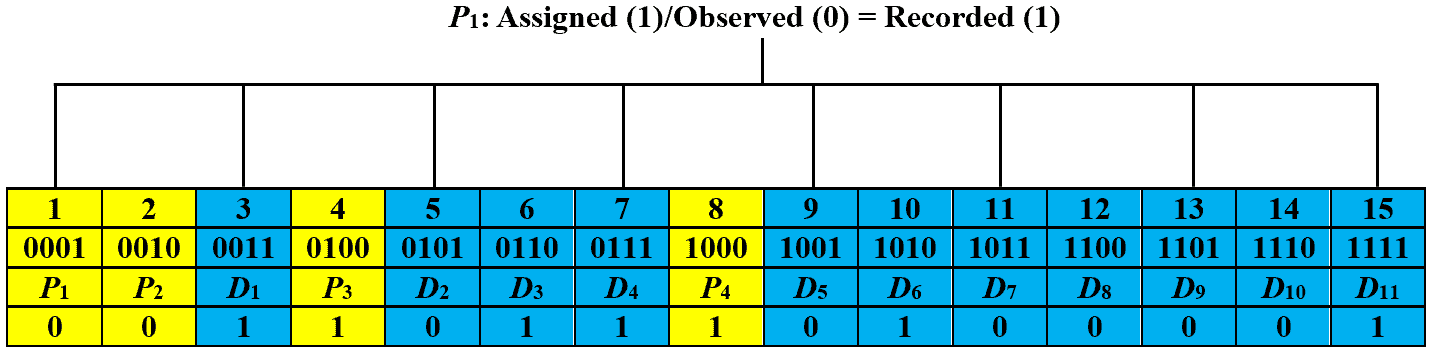
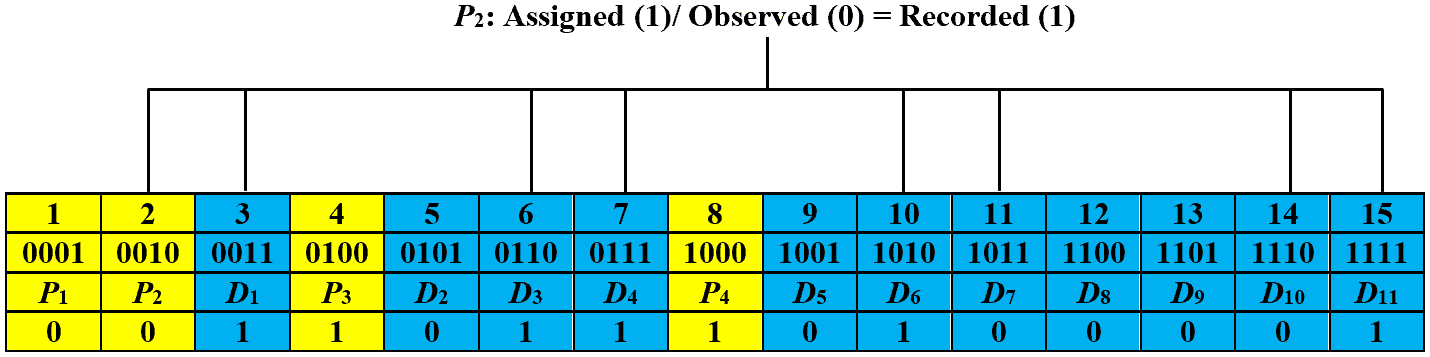
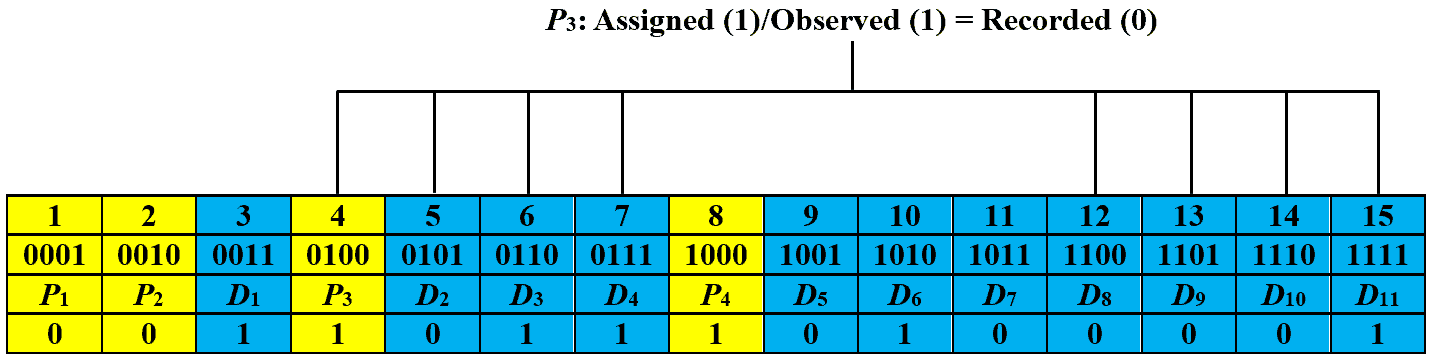
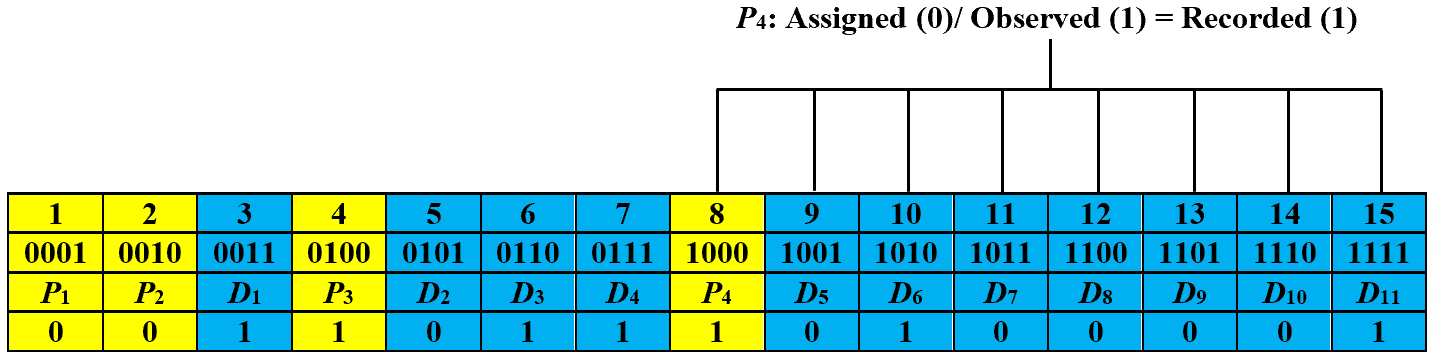
Let’s obtain the checking number by writing the recorded values from right to left, i.e., $P_4P_3P_2P_1 = 1011$ , which is equal to decimal number eleven. This signifies that the received code has an error at the eleventh bit. In order to correct it, we just have to toggle the eleventh bit and the corrected code is:

5. Advantages and Limitations

The key advantages and notable limitations of the Hamming code are:

6. Conclusion

This tutorial first provides a brief overview of the Hamming code and its use cases. It then explains the basic concepts of the Hamming code, such as redundant bits, parity bits, and parity bit calculation.

Next, it presents an illustrative example of encoding a data block using parity bits. Later, it discusses and demonstrates the steps involved in error detection and correction. In the end, it highlights the key advantages and limitations of the Hamming code.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex