1. Introduction
By now, most people are already familiar with ChatGPT: the AI chatbot capable of conversing, answering complex questions, and generating code. On the other hand, most people aren’t as aware of the underlying GPT architecture that allows for the generation of text in a manner that seems realistic.
In this tutorial, we’ll talk about the temperature parameter and how it can be used to modify the text generated by GPT models.
2. What Does Model Temperature Do?
First, let’s go on the official OpenAI playground and choose the gpt-3.5-turbo-instruct model.
Then, we’ll modify the temperature slider in the top-right corner and compare the output for a simple starting sequence like “I enjoy eating”.
We notice that when the temperature has a lower value, closer to 0, it will offer more “conventional” completions, such as “food” or “healthy meals”. If we set the temperature to a middle value, like 1, we still get sentences that make sense, but are more varied, like “italian dishes” or”salads during the summer”. However, if we set the temperature too close to 2, we’ll start getting gibberish that doesn’t even resemble words, something like “how_DIG728 tie_COLL mund196].)”.
In essence, temperature controls the randomness of the generated sequence, which can mean many things: how conventional the sentence is, how opinionated the completion is in a certain direction, if the words used make sense in that context, or even if they’re actual words at all!
3. Why Is It Called Temperature?
In physics, the temperature of a gas determines how much its molecules move around. The hotter it gets, the more chaotic the movement of the molecules becomes. Thus, it’s harder to predict where the molecules will be in a future state. On the other hand, if the gas is cooled down, the movement becomes more predictable. This phenomenon is used, e.g., in Simulated Annealing.
The same principle applies to the “temperature” hyperparameter in GPT: lower temperatures lead to more conservative outputs, while higher temperatures lead to more variation.
4. The Link Between Text Generation and Temperature
Generating a big block of text starting from a short sentence is equivalent to finding the most likely next word and then doing it repeatedly. Language Models solve this exact problem. Let’s take an example to see how they achieve that.
Suppose we have four sentences in our model’s train set. This represents the complete understanding of language that our model has. Naturally, better models use significantly more text than this:
- “I like cats”
- “I like eating sushi”
- “I like eating pizza”
- “I like eating sushi with my friends”
Let’s say the user wants to generate some text to complete the following sentence:
“I like …”
In 1/4 of our examples, the phrase is followed by “cats” and in 3/4 of them it is followed by “eating“. Thus, if we run the model 4 times, it will complete the sentence with “cat” once and with “eating” 3 times (on average).
If “eating” was selected by the model, our new sentence becomes “I like eating …“. Using the same logic again, we have a 1/3 chance of choosing “pizza” and a 2/3 chance of choosing “sushi“.
This example corresponds to the case when the temperature is equal to 1. In the figure below, this is represented with purple:
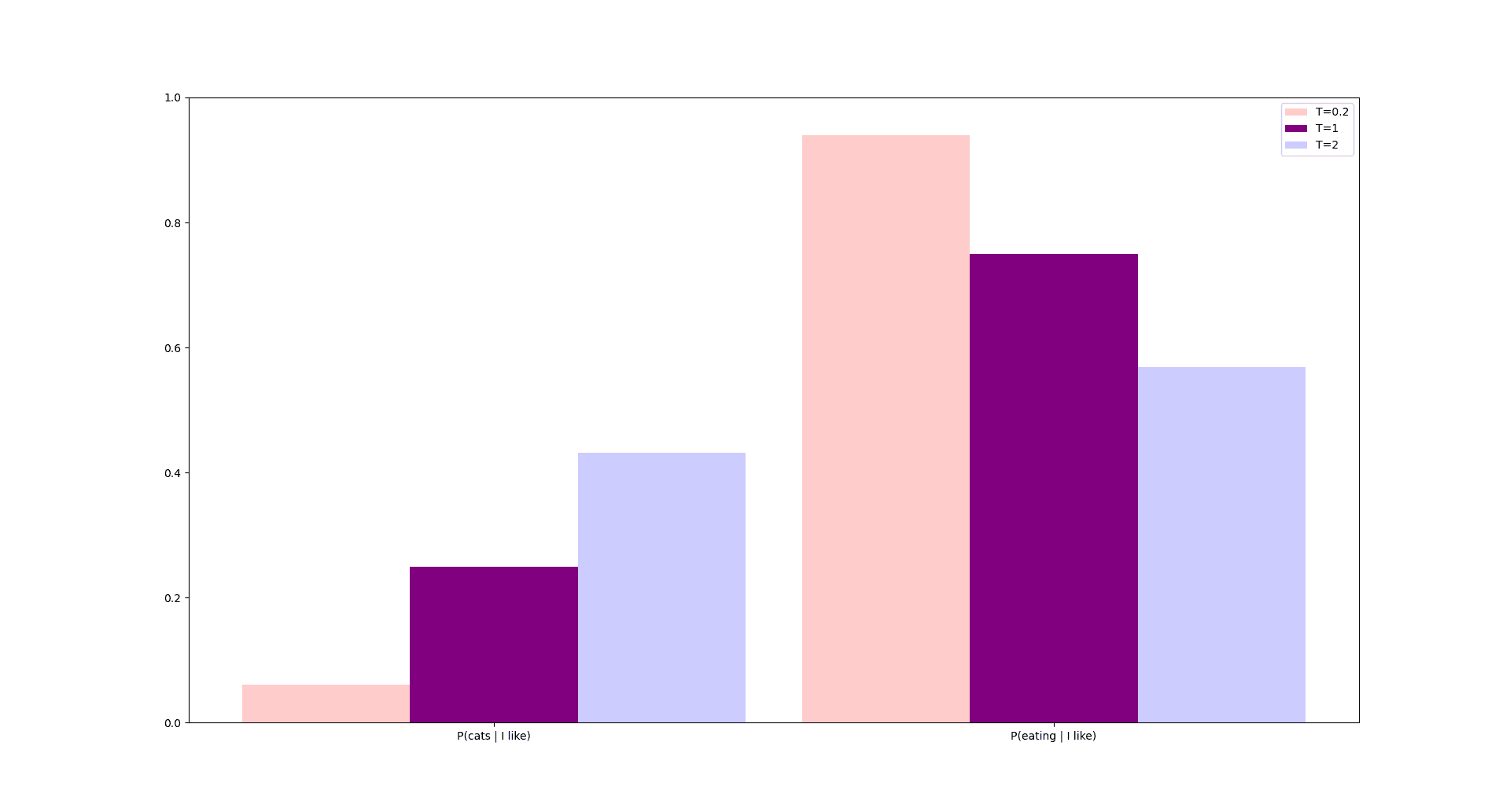
For a temperature closer to 0, our model will tend to choose the most likely sequence way more often than the rest, which leads to it repeating “I like sushi” every time, even if the input is only “I …“. We don’t want this, we also prefer it saying “I like cats” from time to time. In the figure, this is represented with light red.
Conversely, if the temperature becomes big, the model starts ignoring these probabilities. This means it will generate nonsensical sentences such as “I friends cat like my“, even if they don’t appear at all in the train set. In the figure, this is represented with light blue.
Finally, here’s the formula for computing the final probabilities after taking into account the temperature $T$ parameter:
$$ p_i(T) = softmax(log(\frac{p_i}{T})) $$
The formula confirms what we’ve seen graphically:
- If $T$ is 1, the final probabilities are equal to the initial probabilities, as softmax and the logarithm cancel out
- If $T$ is larger, then all initial probabilities shrink significantly, so they end up similar to one another
- If $T$ is closer to 0, the large probabilities become larger, and the small ones become even smaller, so the differences become exaggerated
5. Conclusion
In this article, we discussed how model temperature influences text generation, with lower temperatures corresponding to conventional outputs and higher temperatures corresponding to more random text.
In addition, we explained the mechanism of Language Models and how temperature influences the probability of the next word.