Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: May 11, 2024
When we design a network, we always need to know how many addresses do we need in this network. Also, we would like to know the range of IP addresses in our network so that we can assign an address for each device in the network.
In this tutorial, we’re going to show a simple method to find the range of IP addresses given a subnet mask.
In IPv4, the IP address consists of 32 bits number. And we represent it by 4 octets (8-bits each). Usually, when we refer to a network, we also refer to a subnet. This subnet can be a number (for example /24), and we can write it like an IP address (example /255.255.255.0). From this subnet, we’d like to find out what are the IP addresses in this network.
For example, if we have a network 192.168.0.1/24 (or with subnet 255.255.255.0), then we have 256 usable addresses from 192.168.0.0 up to 192.168.0.255.
In general, if we deal with the IP address as a 32-bit number, and we have a subnet mask of , then the subnet mask theoretically can take values between
. Then, we have two things to estimate, what are the number of possible addresses with the given subnet mask, and what is the starting address.
We can get the number of possible addresses easily by the following formula . That means if we have a subnet mask of
, then the possible addresses are
. And if we have a subnet mask of
, then the possible number of addresses is
, which means the given address is the only possible address in this case. One more example the case of subnet mask of
, we will have
addresses.
Then, we need to interpret this subnet mask in the octets form. If we have a subnetmask of , we are actually having a 32-bit number that has the left most 24-bits as ones and the rest are zeros:
| subnet mask decimal | 24 | |||
|---|---|---|---|---|
| subnet mask binary | 11111111111111111111111100000000 | |||
| subnet mask decimal octets | 255 | 255 | 255 | 0 |
| subnet mask binary octets | 11111111 | 11111111 | 11111111 | 00000000 |
From the previous table, we can see how the subnet mask can be interpreted. So, if we have an IP address like 192.168.0.10/24, we can write it down in a table to show the binary octets compared to:
| IP address decimal octets | 192 | 168 | 0 | 10 |
|---|---|---|---|---|
| IP address binary octets | 11000000 | 10101000 | 00000000 | 00001010 |
To find the starting address in the following subnet mask, we simply do binary “and” operation between the IP address and the subnet mask:
| IP and subnet mask | 192.168.0.10/24 | |||
|---|---|---|---|---|
| IP address binary octets | 11000000 | 10101000 | 00000000 | 00001010 |
| subnet mask binary octets | 11111111 | 11111111 | 11111111 | 00000000 |
| First IP binary octets | 11000000 | 10101000 | 00000000 | 00000000 |
| First IP decimal octets | 192 | 168 | 0 | 0 |
Finally, we calculate the last IP address by applying the “or” operation on it with the bitwise binary inverse of the subnet mask to the first IP address:
| IP and subnet mask | 192.168.0.10/24 | |||
|---|---|---|---|---|
| subnet mask binary octets | 11111111 | 11111111 | 11111111 | 00000000 |
| First IP binary octets | 11000000 | 10101000 | 00000000 | 00000000 |
| inverse subnet mask binary octets | 00000000 | 00000000 | 00000000 | 11111111 |
|---|---|---|---|---|
| Last IP binary octets | 11000000 | 10101000 | 00000000 | 11111111 |
| Last IP decimal octets | 192 | 168 | 0 | 255 |
With these simple steps, we know how to find the number of possible IP addresses. We can also find the first and last IP addresses and the range becomes from 192.168.0.0 up to 192.168.0.255.
The same idea happens if we have a subnet mask that is not exactly at one of the octets. Let’s see and example of 192.168.0.10/30. By following the same idea we have possible IP addresses:
| 192.168.0.10/30 | decimal | binary |
|---|---|---|
| IP address | 192.168.0.10 | 11000000.10101000.00000000.00001010 |
| subnet mask | 255.255.255.252 | 11111111.11111111.11111111.11111100 |
|---|---|---|
| First IP | 192.168.0.8 | 11000000.10101000.00000000.00001000 |
| inverse subnet mask | 0.0.0.3 | 00000000.00000000.00000000.00000011 |
|---|---|---|
| Last IP | 192.168.0.11 | 11000000.10101000.00000000.00001011 |
Let’s take one more example where the subnet mask is not in the last octet like 10.0.0.0/20. In this case we have possible IP address:
| 10.0.0.0/20 | decimal | binary |
|---|---|---|
| IP address | 10.0.0.0 | 00001010.00000000.00000000.00000000 |
| subnet mask | 255.255.240.0 | 11111111.11111111.11110000.00000000 |
|---|---|---|
| First IP | 10.0.0.0 | 00001010.00000000.00000000.00000000 |
| inverse subnet mask | 0.0.15.255 | 00000000.00000000.00001111.11111111 |
|---|---|---|
| Last IP | 10.0.15.255 | 00001010.00000000.00001111.11111111 |
Luckily, in most programming languages, we don’t need to convert between binary and decimal to do the binary operations. So, we can apply the binary operations directly on most countable numbers (like integers or chars). In other words, we can represent the IP address by a 32-bit number or using digits 8-bits each (like characters or bytes).
In IPv6, the same idea for the subnet is similar to the IPv4. But the difference is in the size of the address and the allowed range. The IPv6 address has bits compared to
bits in IPv4. The address is represented in
segments compared to
octets in the IPv4. Each segment is 4 hex numbers taking range from
to
compared to 8-bits per octet in IPv4 with the decimal range
to
. The separation between blocks in IPv6 is a colon (:) compared to dot (.) used in IPv4.
In general, we can get the number of the available IP addresses the same way we did it in IPv4. So, if we have a subnet of size , then we have
available IP addresses. And we can get the first one of them by applying bitwise and with a mask of size
bits, where the first
bits are ones and the rest are zeros. And we can get the last address by adding the first address to the inverse of the mask (
bits with the first
bits as zeros and the rest are ones).
Let’s see an IPv6 example for . Notice that each segment is written as 4 hex digits which equal 16-binary bits. The number of addresses will be
:
| hex | |
|---|---|
| IP address | 2001:124A:2000:1000:0000:0000:0000:0000 |
| subnet mask | FFFF:FFFF:FFFF:0000:0000:0000:0000:0000 |
|---|---|
| First IP | 2001:124A:2000:0000:0000:0000:0000:0000 |
| inverse subnet mask | 0000:0000:0000:FFFF:FFFF:FFFF:FFFF:FFFF |
|---|---|
| Last IP | 2001:124A:2000:FFFF:FFFF:FFFF:FFFF:FFFF |
Notice that is equivalent to
ones
. Another note is that the IPv6 address can also take short forms by removing leading zeros in any segment.
Thus, we write our example first address:
And another shortened form is to replace one of the sequences of empty segments (all zero segments) with a double colon. So, the other shortened form of this address becomes:
Note that the shortened version does not allow more than one time for omitting the zeros segments. So, if we have and address:
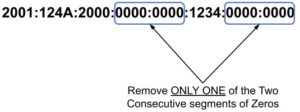
The shortened version will be:
Or:
In this shortened version, we can know how many zeros are removed because we know that we have 128 bits divided into 8 segments. Thus, we know how many segments are removed from the 8 and these are the zeros omitted.
The time and space complexities of finding the range of IP addresses are because we just need to put the subnet mask in a formula to find the range.
In this article, we have explained a simple method to estimate the range of possible IP addresses from the subnet mask.