Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: July 18, 2024
In this tutorial, we’re going to explore the topic of generating crossword puzzles. Which is effectively placing a set of words into a grid, such that they overlap.
In particular, we’ll be focusing on how to determine where to place words to generate the best crosswords.
Our starting algorithm is to place words iteratively into a grid until we run out of space. This will work by shuffling our word list and then working down it and placing each one onto the grid until we have reached a set number of words to place.
Note that this algorithm assumes an infinite grid where we can place words. In reality, this obviously can’t be the case, and any implementation would need to work within our constraints.
algorithm IterativePlacement(words, maxWords):
// INPUT
// words = list of words to place on the crossword
// maxWords = the maximum number of words to place
// OUTPUT
// crossword = the generated crossword grid
shuffle(words)
word <- pop(words)
crossword <- place(word, null, 0, 0, HORIZONTAL)
count <- 1
while count < maxWords and len(words) > 0:
word <- pop(words)
for letter in word:
for y in rows(crossword):
for x in cols(crossword):
if crossword[y, x] = letter:
placement, ok <- canPlace(word, crossword, x, y)
if ok:
crossword <- place(word, crossword, placement.x,
placement.y, placement.direction)
count <- count + 1
continue
return crosswordA lot is going on here, and not everything is expressed in the above algorithm. In particular, the mechanisms for placing a word and checking if a word is legit are omitted for brevity.
Our first word is just placed in the middle of the grid. All other words then expand from there.
Subsequent words will find a location by iterating over each letter in the word and then iterating through the grid to find a position that has this letter in it. We check if the word can legally be placed here whenever we find one. We keep going until the first of these checks passes, in which case this is where we stop and place this word.
Sometimes, there are no suitable slots. For example, there might be no letters in common, or there might be no places that legally allow the word to be placed. Then, we keep going until we have either placed enough words or have run out of words.
Let’s work through this algorithm and see it in action to show how it can create our first crossword.
Our first randomly selected word is “SHOP”. This gets placed directly on the grid, giving us:

After this, we start with the bulk of the algorithm.
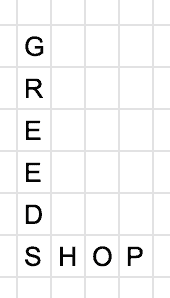
The next word is “GREEDS”. We’ll iterate over every letter in the word and each letter over every cell in the crossword until we find our first match. In this case, the “S” at the end of “GREEDS” matches the “S” at the start of “SHOP”.
Next, we check if we can place the word here – i.e., will it interfere with any other words negatively – and if we can place it, we determine where it will start and the direction it will go.
Finally, we add it:
The next word that we pull from our list is “FAINT”. This word can’t be placed and will just be skipped over. After iterating over every letter in this word, and every cell on our crossword grid, we don’t find any matches at all.
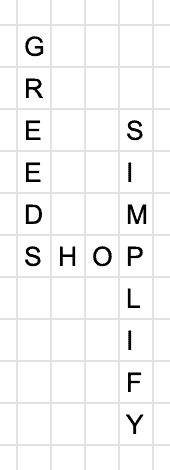
Next, we get “SIMPLIFY”. Out first potential slot is with the “S” at the start of “SHOP”. However, we can’t place the word here because it would conflict with the word “GREEDS”. As such, we keep scanning the cells until we find that the “P” in “SIMPLIFY” matches the “P” in “SHOP”.
This is the right place – it doesn’t interfere with any other words – and so we can add it here:
We can then repeat this process for each subsequent word until we run out of words or we have reached a certain number placed on the grid:

At this point, we have our completed crossword.
So far, we can generate a crossword grid, and our first attempt worked quite well. However, a different set of words might generate something less impressive:

In this case, the cause was down to the randomly selected words in our crossword.
We can improve the overall result by generating many crossword grids and selecting the best one.
If we have a way to score crosswords, we can simply generate many grids, score each one and keep only the highest scoring:
algorithm RepeatedGeneration(words, maxWords, iterations):
// INPUT
// words = the list of words to be placed in the crossword
// maxWords = the maximum number of words to place in the crossword
// iterations = the number of crosswords to generate for comparison
// OUTPUT
// crossword = the crossword with the highest score from all generated crosswords
maxScore <- 0
result <- null
for i <- 0 to iterations:
crossword <- generate(words, maxWords)
score <- generateScore(crossword)
if score > maxScore:
maxScore <- score
result <- crossword
return resultWhen doing this, we can either repeat the loop a given number of iterations for a given amount of time – maybe we want to get the best crossword that we can generate in 5 minutes – or the first one with a score above a specific value.
Or even some combination of these – we might want the first crossword with a score above a particular value or the best we can generate in 1 thousand iterations, whichever comes first.
Once we generate many crosswords, we need to decide what “best” means. This depends on the type of crosswords that we want to generate, but it could include:
Or anything else you want to use. The only important detail is that every crossword is scored similarly.
For example, a scoring algorithm that selects for denser, squarer crosswords might be something like:
algorithm GenerateScore(crossword):
// INPUT
// crossword = the crossword grid
// OUTPUT
// score = the calculated score of the crossword
sizeRatio <- rows(crossword) / cols(crossword)
if rows(crossword) > cols(crossword):
sizeRatio <- cols(crossword) / rows(crossword)
filled <- 0
empty <- 0
for y in rows(crossword):
for x in cols(crossword):
if crossword[y, x] = null:
empty <- empty + 1
else:
filled <- filled + 1
filledRatio <- filled / empty
return (sizeRatio * 10) + (filledRatio * 20)Here we generate a score that is:
If we apply this to the two grids that we’ve seen so far, we’ll see that the first one has a score of “21.92672999“, and the second will have a score of “12.3653512“, so our first grid is clearly better.
We now have a general algorithm for placing words into a grid, repeating this many times, and selecting the best result. But this will always produce the grids in the same way – placing a new word in the first place that it fits.
For example, our second grid placed “UNAPPROVED” coming from the “U” in “ODIOUS”, because that’s the first place that the first letter fits. This might not always be the best place to put the word.
It might be better to have instead placed it crossing at the “O” instead:

This produces a square crossword – 10 x 6 instead of 14 x 6 that we had before – which is more desirable by our scoring algorithm.
We already have a means to determine which of a set of crosswords is “best” – our scoring algorithm. We could use this by placing the new word in every possible place and generating a score for each. We then use the placement that produced the highest score:
algorithm RepeatedWordPlacement(words, maxWords):
// INPUT
// words = a list of words to place in the crossword
// maxWords = the maximum number of words to place in the crossword
// OUTPUT
// crossword = the generated crossword
shuffle(words)
word <- pop(words)
crossword <- place(word, null, 0, 0, HORIZONTAL)
count <- 1
while count < maxWords and len(words) > 0:
word <- pop(words)
placements <- [ ]
for letter in word:
for y in rows(crossword):
for x in cols(crossword):
if crossword[y, x] = letter:
placements <- append(placements, findPlacement(word, crossword, x, y))
bestScore <- 0
bestBoard <- crossword
for placement in placements:
newBoard <- place(word, crossword, placement.x, placement.y, placement.direction)
newScore <- generateScore(newBoard)
if newScore > bestScore:
bestScore <- newScore
bestBoard <- newBoard
if bestScore > 0:
crossword <- bestBoard
count <- count + 1
return crosswordThis works by first finding every single placement for the new word, then iterating over each one to find the one that produces the best new score. This board then becomes the new one to use.
Applying this to the placements of “UNAPPROVED”, we find that we get a score of “12.10702341” when it starts from the “U” in “ODIOUS”, and a score of “15.26829268” when it crosses at the “O” instead, so this is the better place to put it.
However, if it instead crossed at the “A” in “MANIA” then we get a score of “17.25806452” which is even better:

So far, this will find the best placement for any given the word. However, a suboptimal placement for one word may ultimately lead to a better overall result. For example, our above board was the best placement for the word “UNAPPROVED” but has resulted in several letters being very difficult, if not impossible, to place words from.
We could potentially improve on this by building a deeper tree of options. We can generate not only every possible placement for this word, but for each of those every possible placement for the next word, and keep going to a certain depth. Then we select the node at the top of the tree that leads to the best score at the bottom. This is similar to other search algorithms that we’ve explored in the past and can give excellent results.
Here we’ve seen some algorithms for generating crossword puzzles and explored how each one helps to improve on the previous and what can be further done.
Why not try implementing the tree search algorithm and see what puzzles you can come up with.