1. Introduction
In this tutorial, we’ll explore a few techniques for the procedural generation of maps, such as in a computer game. These are maps that are entirely random and so give much better variety for gameplay, and yet are still relatively realistic.
2. What Is Procedural Generation?
Many times in computer games, we want to give the impression of significantly more content than we can actually produce or store. Either because of restrictions in the production of the content in the first place – e.g. for a small production team – or else in the storage or distribution of the content.
We can get around this, though, with Procedural Generation. This is when the game generates new content on the fly at runtime instead of only using previously produced content. Done right, this can give us effectively limitless content in our game with much lower production costs up-front.
All procedural generation depends on being able to reliably produce random numbers. Depending on the exact need, we might also need to be able to produce the same sequence of random numbers over and over – i.e. use the same starting seed and the same algorithm to give the same stream of numbers. The various procedural generation algorithms than just do different things with these random numbers as appropriate.
3. Random Piece Allocation
One very simple method of generating maps randomly is to allocate previously generated pieces of content randomly. This can work especially well for buildings, spaceships, dungeons and other similar areas, but done right. We can use this for many map types.
For this to work, we need a suitable set of pieces that we can work with. Each piece must be of a known size and with known join points. For example, if we’re generating a building, then each piece could be a room, and the join points could be doors. We might also have some additional restrictions on certain pieces. For example, the first piece might be from a restricted set with the main doors, and certain edges of certain pieces might be outside walls and can’t be extended further.
This algorithm then repeatedly selects a point on the current map that we want to extend and then selects a new piece with which we want to extend it. We keep going until we’ve got a big enough map or we’ve got no more suitable pieces to use:
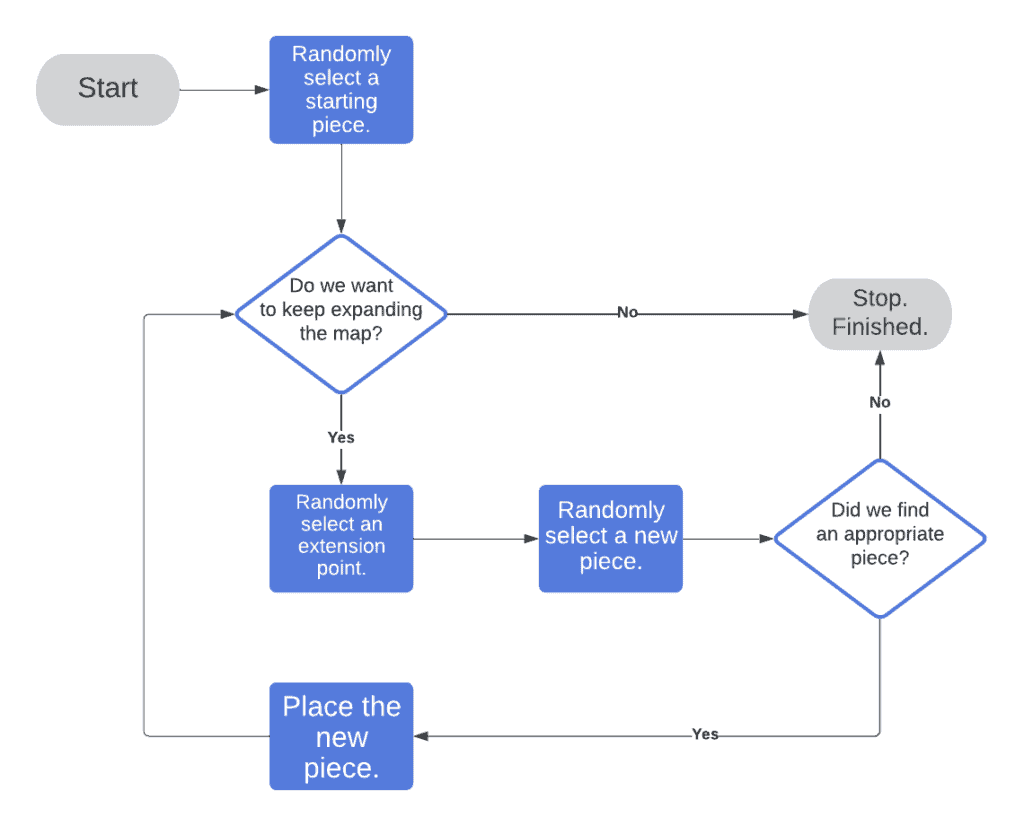
This seems very simple, but what does it look like?
Here we’ve randomly generated a building structure. We started with the entrance hall – which is the only piece placed that has doors opening from the outside. We’ve then repeatedly selected the next place to position something, and the next piece to place, until we’ve got a layout that we’re happy with.
In this example, we’ve shown just simple room outlines. But in practice, the pieces could be fully populated. Instead of laying down just room outlines, we could’ve laid down a kitchen, a sitting room, a conservatory and so on. All of which are fully modelled and ready to use. This would then give a high-quality map that has been randomly generated and will be different for every player.
4. 2D World Generation
We’ve just seen how we can generate a totally unique map from pre-existing pieces. However, this still requires those pieces to have been previously created. That, in turn, means an amount of production work needs to be done ahead of time.
What if we want to instead generate a world map? Theoretically, we could do this in a similar manner. However, we can use other techniques to give us a more varied and unique landscape with less production work needed ahead of time.
When generating a 2D world, our main objective is essentially to draw a single line from left to right. This line acts as our ground. Everything above is the sky, and everything below is the land:
However, this is a pretty boring map. We want something more interesting, so we want to adjust the height of our land across the landscape.
4.1. Random Height Offsets
The naive approach to this is to just randomly shift it up or down a little bit for every pixel:
For example, let’s use this to draw a landscape of length 500 pixels, with an initial height of 150 pixels and random variability between -10 and +10 pixels on each step.
This works. It looks more interesting, but it doesn’t look very realistic. The map is too jagged and spiky. We also have the risk of the landscape running away from us – feasibly, it could just go up or down too far:
4.2. Height Dependant Offsets
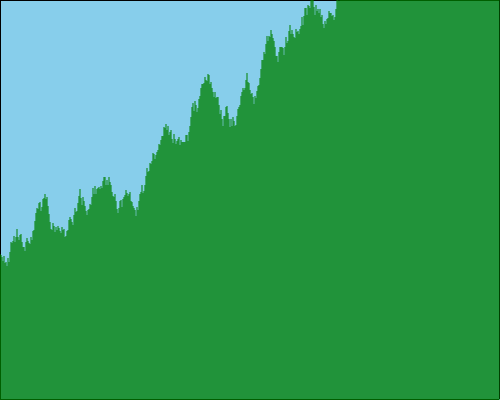
One option we have for tackling this is to adjust our offsets based on the distance from the baseline. This will then give us much smoother extremities and will also make it impossible to shift too far from our starting point:
If we use this with a variability cap of 200, then we might get something like this:
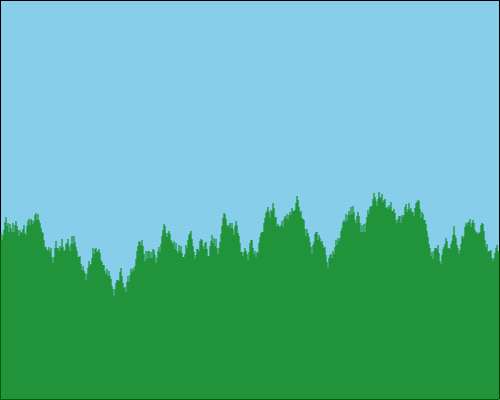
So we’ve removed any extremes in deviation, but we still have a very jagged appearance.
4.3. Interpolation Between Points
Let’s attempt to sort out this jagged appearance. One way that we can do this is to generate fewer points spread much further apart, and then generate intermediate points between them to generate smooth curves:
If we do this with a gap between our generated points of 20 pixels – meaning that we have 25 segments – then we might get something like this:
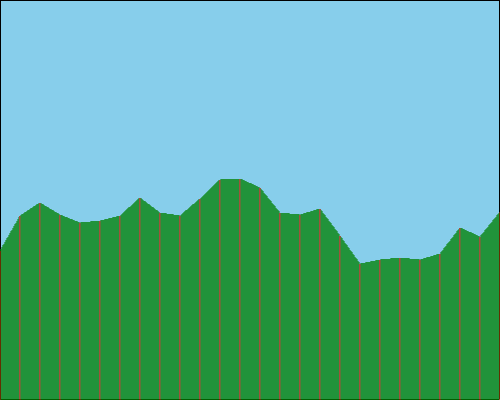
We can immediately see that we have a much smoother appearance. And how this looks can be adjusted by changing how we interpolate between our points. For example, we could choose to draw curves between a set of points instead of just straight lines between adjacent points.
5. 3D World Generation
We’ve seen how to generate a realistic-looking 2D map, but what about a 3D map? What we’ve just seen is a simplification of Perlin Noise. This is a technique developed by Ken Perlin in 1983 to generate gradient noise, which gives a random yet realistic-looking pattern of heights.
Perlin Noise first generates a coarse grid of random gradient vectors overlaying our map. We can then compute a value for any position in our map such that the transitions between points will always be smooth. This is done by:
- Determining the grid cell that our point is within, and thus the corners of this cell.
- For each corner:
- Generate an offset vector from this corner towards our point.
- Calculate the dot product of this offset vector and the random gradient vector for this corner.
- Interpolate all of these calculated dot products together to gain the height for this point.
This can be done in any number of dimensions, but we’ll work in 2D here. We’ll then treat every point on our 2D perlin noise as the height of the corresponding position in our 3D world:
This will then give us something like this:
This doesn’t look like much, but let’s try colouring it in a bit:
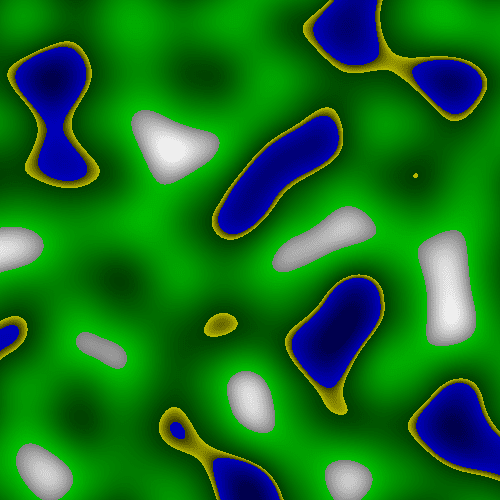
Suddenly, this looks like a realistic map.
5.1. Perlin Noise Algorithm
So, how does this all work? The overall algorithm for perlin noise is:
The first thing we need to do is generate our random grid. This is a grid of random gradient vectors that overlays the map but is much coarser. The exact way this works isn’t important, but here we’re generating a random angle 
and then using trigonometry to calculate the 
and 
values for our vector.
This has the advantage that we’re only generating a single random number per point and that we’re guaranteed to generate a unit vector:
After this, we start calculating values for every map point. From here on, there’s no randomness left. Everything is just calculating some values based on our random gradients and the relative positions on the map to them. This means that we can potentially store the random grid and just compute every map value on demand.
For each point on the map, we first need to determine which cell in our grid we’re in, and where we are within that grid cell. Ultimately this leaves us with two vectors for each corner of the grid cell that we’re in. The first is the random gradient vector for that corner, and the other is a vector from that corner to our position in the cell:
Having done this, we compute the dot product for each pair of vectors that we have. We then interpolate these dot products together based on the appropriate position within the grid cell that they came from. At the end of this, we have a single value left, which is used as the height for this map position.
This uses the Smoothstep function for interpolation since this gives a smoother transition between cells. However, we can use any interpolation function that we want to combine our values.
5.2. Worked Example
This seems complicated, so let’s work through it for real. Specifically, we’ll work out the values for this map position:
This is position 
in our overall map. We have a grid of size 
overlaying our map, so our grid cell for this looks:
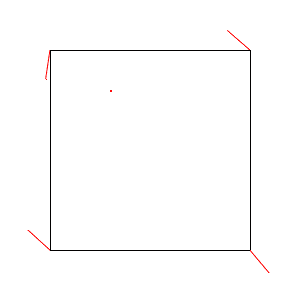
For this cell, our random vectors on the corners are:
- Top left –
- Top right –
- Bottom left –
- Bottom right –
And our offset vectors are:
- Top left –
- Top right –
- Bottom left –
- Bottom right –
From these, we can compute our dot products:
- Top left –
- Top right –
- Bottom left –
- Bottom right –
Finally, we interpolate these values together for our final value:
- FadeX –
- FadeY –
- Top –
- Bottom –
- Final result –
So we have calculated a height value for this map point of 0.1873.
If we follow this process for every single map point, we’ll have generated our height map. We can then normalize these – by finding the highest and lowest values calculated and scaling every point based on those – so that we can understand what the map really looks like. For example, on our above map, the lowest calculated value was 
and the highest calculated value was 
. This means that this exact point normalises to 
in a range of 
to 
.
Our above coloured-in map was done by treating everything with a value below 
as water, below 
as sand, below 
as grass and everything above as mountainous. So, means it’s on the higher end of grassland.
6. Summary
Here we’ve seen some techniques for the procedural generation of maps. A huge variety of such techniques and many more variations are within them. Further, we can mix and match as appropriate.
For example, we could use perlin noise to generate a landscape and then populate it with buildings generated using random piece allocation. Why not try this out for yourself and see how it goes?