Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: February 28, 2025
In this tutorial, we’ll introduce focal loss and describe how it addresses the challenges associated with imbalanced datasets. First, we’ll introduce the area of imbalanced datasets, and then we’ll introduce the definition of focal loss along with its advantages and applications.
Traditionally, when training a machine learning model for classification, we use the cross-entropy loss function that measures the difference between two probability distributions for a given random variable or set of events.
However, we observe that the cross-entropy loss faces considerable difficulties when dealing with imbalanced datasets. More specifically, we refer to a dataset as imbalanced when there is a substantial disproportion in class sizes. For example, medical datasets are usually imbalanced since they contain more samples from healthy than sick patients since there are more healthy patients in the general population.
In these cases, training with cross-entropy can lead to models that disproportionately favor the majority class, resulting in suboptimal performance for minority classes. To deal with this problem, focal loss has been proposed to introduce a dynamic balancing mechanism in the loss function during training.
First, let’s dive into the motivation behind the success of focal loss in dealing with imbalanced datasets. In particular, focal loss introduces a modulating factor that adjusts the contribution of each sample in the total loss. This gives more weight to learning through challenging instances, resulting in better performance. It was introduced by Lin et al. in 2017 and is defined as follows:
(1)
where corresponds to the predicted probability of the ground truth,
denotes the modulating factor to deal with imbalance, and
serves as an additional parameter to control the rate at which easy samples are handled. Below, we can see a visual illustration of the focal loss compared to the traditional cross-entropy when
:
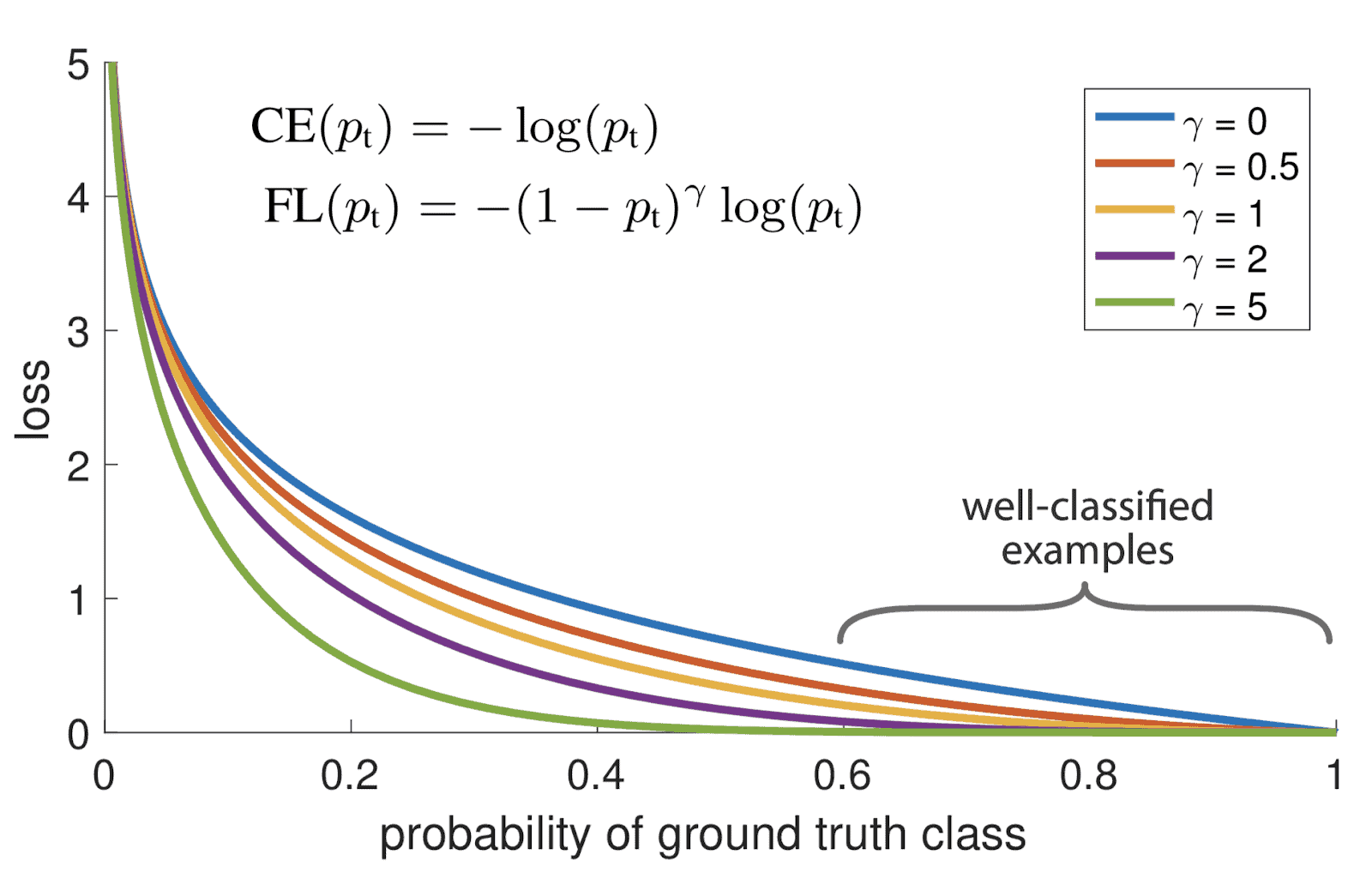
Focal loss provides many advantages compared to the traditional cross-entropy loss.
First, as mentioned before, it enables the ML model to learn meaningful features from imbalanced datasets even when the size of the minority class is very small. Also, it can be used when the ground truth values may contain mistakes due to human annotation. In addition, the concept of focal loss is easy to understand and implement without adding additional computation load in the training procedure. Finally, it contains two hyperparameters ( and
) that provide much flexibility in different domains.
Finally, let’s talk a bit about the use cases and the application of focal loss.
First and foremost, focal loss has proven vital in addressing challenges posed by imbalanced datasets in object recognition applications. Specifically, when training a model to recognize an object, most training images do not contain the desired object, leading to high imbalance.
Predicting rare pathological conditions is highly challenging due to inherent class imbalance. In parallel, annotating medical datasets usually comes with some uncertainty, adding noise to the ground truth labels. As a result, training ML models using the focal loss in these domains is very beneficial and improves the final performance and robustness.
Finally, a strong imbalance exists in sentiment analysis tasks since the presence of some emotions like disgust or fear is less common than happiness and sadness. The ability of focal loss to adaptively adjust its emphasis based on the difficulty of samples makes it invaluable in the scenarios.
In this tutorial, we described focal loss and how it deals with imbalanced datasets. First, we introduced the term imbalanced datasets, and then we denoted the focal loss function along with its advantages and applications.