Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll explain the extended Euclidean algorithm (EEA). It’s a tool widely used in cryptography and one of the fundamental algorithms in number theory. In addition to its recursive version, we’ll present its iterative variant.
Bézout’s identity states that the greatest common divisor (GCD) of any two integers is their linear combination. So, if is the GCD of
and
, then there exist integers
and
such that:
(1)
For example, if and
, then
and:
The extended Euclidean algorithm (EEA) finds and
, which are called Bézout’s coefficients of
and
. As we’ll see, EEA is a modification of the Euclidean algorithm for finding the GCD of two numbers.
In what follows, we’ll assume that and
are both positive and that
. We lose no generality under those assumptions because:
which means that we can consider only the case :
The Euclidean algorithm (EA) finds the GCD of and
by using the fact that:
and applying Euclidean division until it gets zero as the remainder:
The last nonzero remainder () is the GCD of
and
. As we see, the recursion is:
(2)
where . We’ll find it useful to re-formulate the recursive rule so that we express the remainder in terms of the dividend and the divisor:
(3)
The recursive extension of EA (REEA) runs just like the regular EA until it computes , the GCD of the input numbers
and
. At that point, it starts recursing back to the beginning, revisiting the division steps of
backward. After backtracking to a division step, REEA expresses the GCD as a combination of the step’s divisor and dividend.
So, from the second-to-last division, we get:
Now, backtracking to , we replace
with
, so we have:
In general, let’s say we revisited the division step and expressed
as a linear combination of
and
:
(4)
Recursing one step back, we substitute with
in Equation (4):
(5)
Therefore, we obtain the following backward recursive rules:
(6)
We apply them going backward through the division steps until we finally represent the GCD as a linear combination of and
:
algorithm RecursiveExtendedEuclideanAlgorithm(a, b):
// INPUT
// a, b = two non-negative integers
// OUTPUT
// d = the greatest common divisor (GCD) of a and b
// x, y = integers such that d = x * a + y * b
if b = 0:
d <- a
x <- 1
y <- 0
return (d, x, y)
q <- floor(a / b)
r <- a mod b
(d, x, y) <- RecursiveExtendedEuclideanAlgorithm(b, r)
return (d, y, x - q * y)Let’s say that and
. Applying the algorithm, we do five Euclidean divisions:
Or, using recurrence (3):
After identifying the GCD, we go backward one division step. From there, we get and climb one step up to see what to substitute
with:
After some elementary algebra, we get that . Then, we go up a step again to see what to replace
with:
and get . In the end, we backtrack to the first division step:
and obtain Bézout’s coefficients:
(7)
We can compute the coefficients without backtracking. The idea is to express each step’s remainder as a linear combination of and
. To do so, we start by noting that:
In general, we’ll have:
(8)
and we want rules for calculating the coefficients in a step given those from the previous steps. As it turns out, we need only the coefficients from the previous two steps. So, let’s suppose that we know ,
,
, and
for some
:
Using Equation (3), we get:
(9)
Hence, these are our forward recurrences for the coefficients:
(10)
We start from and
and gradually work our way through division steps until we calculate the GCD, at which point we also obtain the sought Bézout’s coefficients:
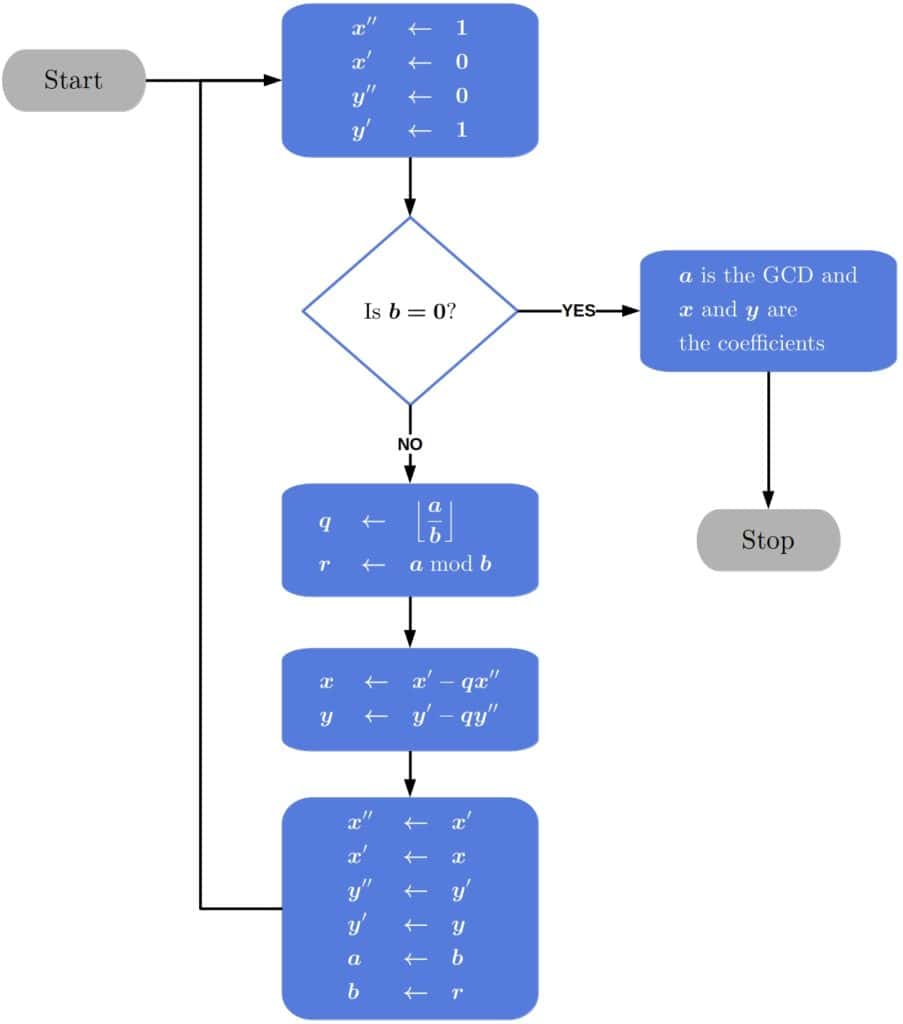
algorithm terativeExendedEuclideanlgorithm(a, ):
// INUT
// a, b = two positive integers
// OUTPUT
// d = the GCD of a and b
// x, y = the coefficients such that d = GCD(a, b) and d = xa + yb
// x``, x`, y``, and y` correspond to x_k, x_{k+1}, y_k, y_{k+1} in recurrences (10)
x`` <- 1
x` <- 0
y`` <- 0
y` <- 1
while b > 0:
q <- a div b
r <- a mod b
x <- x` - q * x``
y <- y` - q * y``
x`` <- x`
x` <- x
y`` <- y`
y` <- y
a <- b
b <- r
d <- a
return (d, x, y)This is how it’ll look like step by step:
This iterative form of the EEA is equivalent to the Blankinship method for two numbers, which extends EA to find the GCD and Bézout’s coefficients of numbers, not just two.
Let’s reuse the example for REEA. Here, we compute the coefficients as we perform Euclidean divisions. The first remainder, , is a direct linear combination of
and
:
Next, we divide with
. Then, we express the remainder
as a linear combination of
and
and replace
with the expression we got in the previous step:
We obtain the coefficients by repeating the step. After each division step, we express the remainder in terms of the current dividend and the divisor. Since both have appeared as remainders previously, we replace them with the corresponding linear combinations and simplify the expressions:
We get the same result as with REEA in the end, but without recursion. Generally, the iterative variant should be faster because it avoids recursive calls and keeps the same frame.
As we see from the recurrences (10), the -coefficients and
-coefficients don’t depend on one another. Moreover, from the final form:
we can calculate the final if we know the final
:
and the other way around. So, there’s no need to compute both coefficients as we make division steps. That cuts the number of operations by a third.
Bézout’s coefficients are not unique, In fact, if is one pair of Bézout’s coefficients for
and
, then all the coefficients are of the form:
(11)
where .
Only two pairs satisfy:
(12)
and EEA always finds one such pair.
In this article, we presented the recursive and iterative forms of the Extended Euclidean Algorithm. It’s used for finding Bézout’s coefficients of two integer numbers and has applications in cryptography.