Explanation of the Number e (Euler’s Number) | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll explore Napier’s constant, also known as Euler’s number, denoted by the symbol $e$ . It’s equal to approximately 2.71828.

This remarkable number is not only a key element in mathematics but also a ubiquitous element in a wide range of natural phenomena and scientific laws.

Originally introduced by John Napier in the context of logarithms, the significance of $e$ transcends its historical origins, weaving its way through various branches of mathematics and science. We’ll see some examples that illustrate the deep connection between $e$ and real life.

2. Characteristics of e

Let’s take a look at the irrationality and transcendence of $e$ , concepts far removed from our intuitive understanding.

2.1. e Is Irrational

An irrational number is one that can’t be expressed as a fraction of two integers. In other words, its decimal representation is non-repeating and infinite:

$e = 2.7182818284590452353602874713526624977572470936999595749669676277...$

Euler himself first proved the irrationality of $e$ in 1737. Further demonstrations were made later by Joseph Fourier and other nineteenth-century mathematicians.

2.2. e Is Transcendental

Charles Hermite proved the transcendence of $e$ in 1873, and this property elevates $e$ to a level of complexity even beyond that of simple irrational numbers. The concept of transcendental numbers can be quite abstract, but it tells us that $\boldsymbol{e}$ can’t be constructed by basic algebraic operations alone.

More precisely, $e$ isn’t the solution of an equation of the form $a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 = 0$ , where $a_0, a_1, \ldots, a_n$ are rational numbers and $n$ is a positive integer.

3. Brief History and Definitions of e

The study of $e$ begins with John Napier (1550-1617), best known for his work on logarithms. While Napier’s work focused on simplifying calculations, it indirectly set the stage for the discovery of $e$ by introducing concepts fundamental to exponential growth:

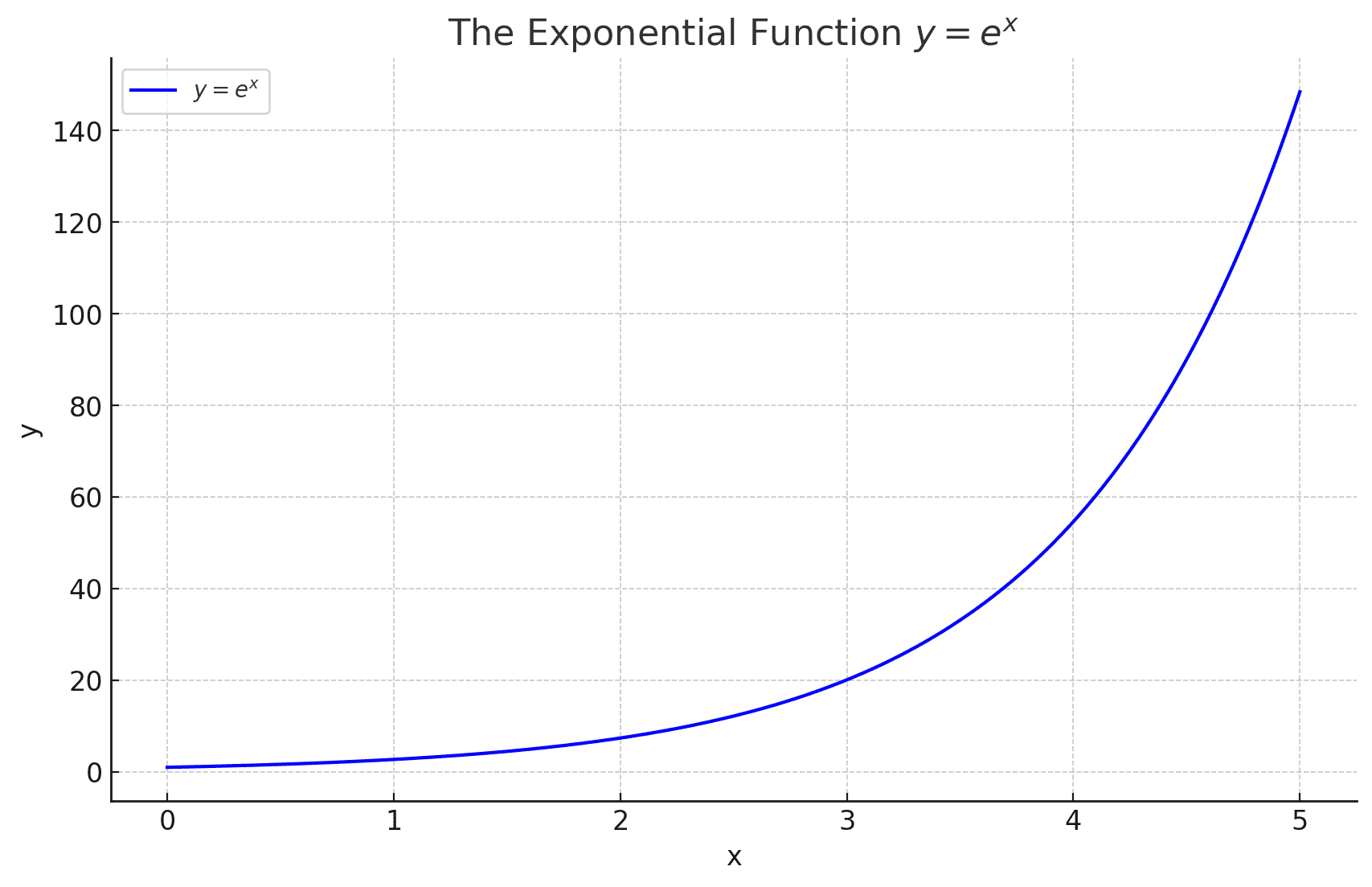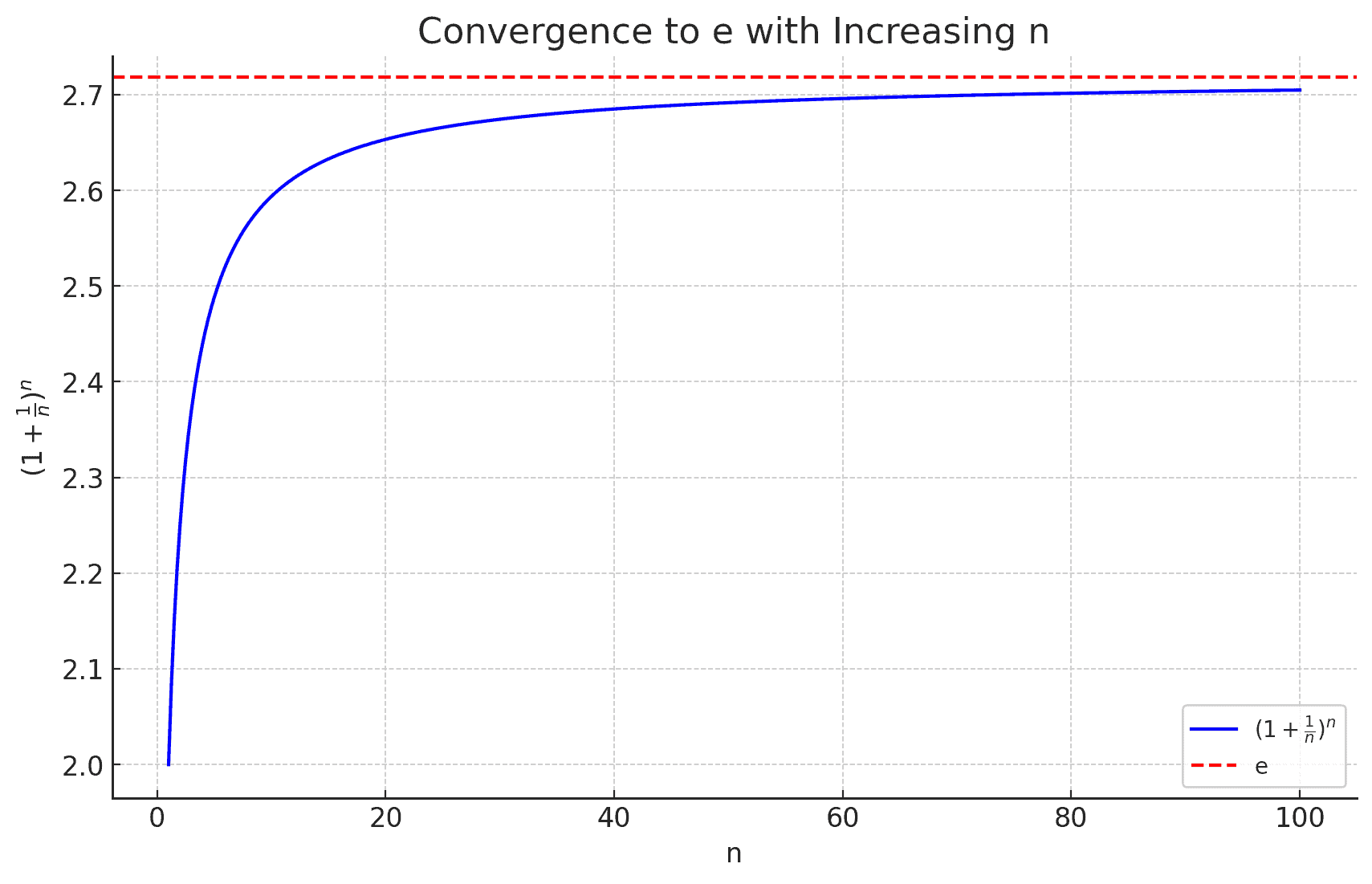
Jakob Bernoulli (1654-1705) brought $e$ into sharper focus in financial mathematics through his work on compound interest, defining $\boldsymbol{e}$ as the limit of $\boldsymbol{(1 + \frac{1}{n})^n}$ as $\boldsymbol{n}$ tends to infinity:

Leonhard Euler (1707-1783) played a crucial role in the formalization of $e$ , not only by popularizing the notation, but also by connecting it to various mathematical domains. Euler’s formula $e^{ix} = \cos(x) + i\sin(x)$ links $e$ to trigonometric and complex functions, demonstrating its fundamental importance. In addition, Euler provided a series expansion, $\boldsymbol{e = \sum_{n=0}^{\infty} \frac{1}{n!}}$ , giving a direct definition for $\boldsymbol{e}$ and further illuminating its properties:

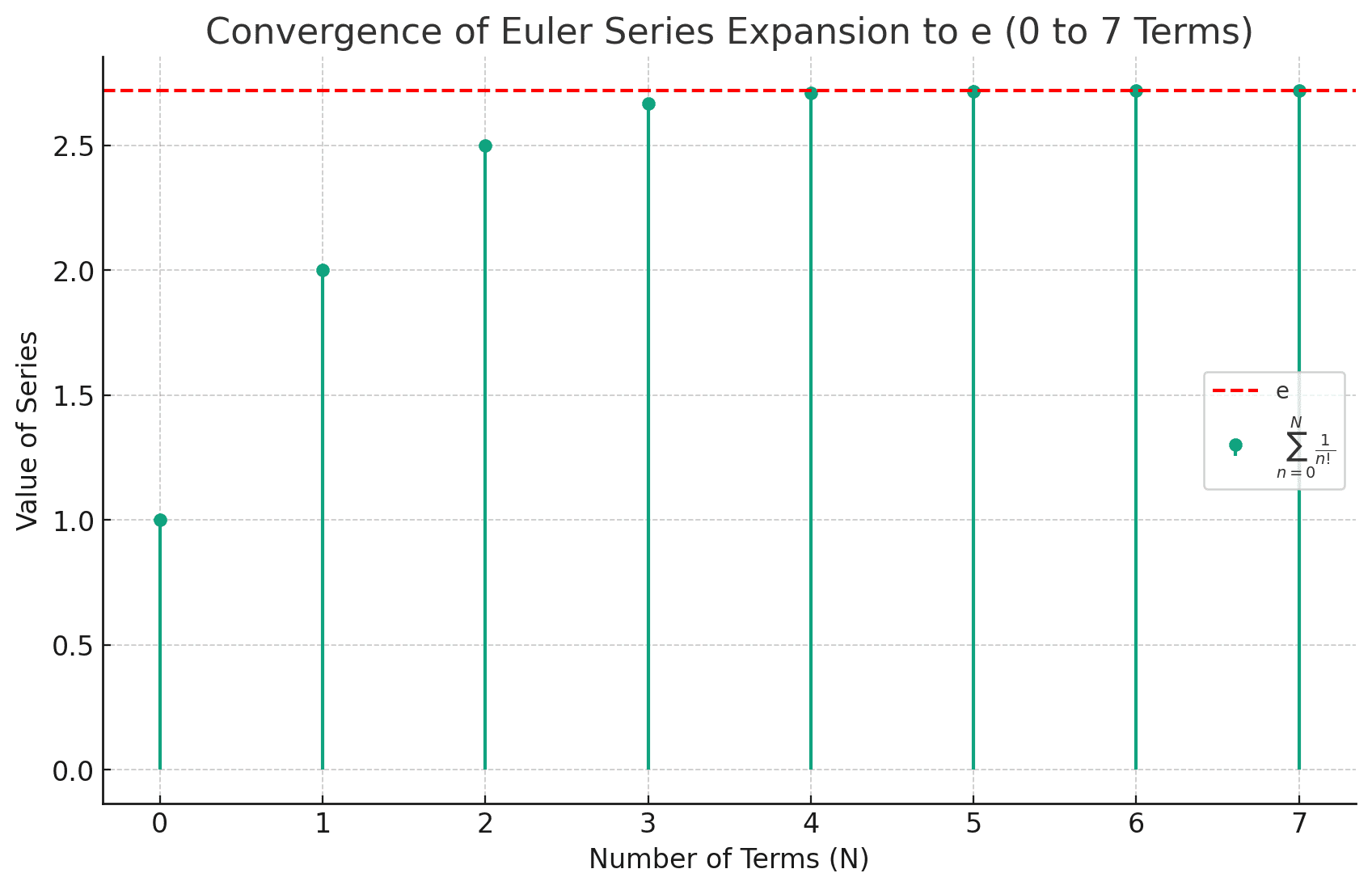The convergence to $e$ , marked by the red dashed line, is evident even with a relatively small number of terms, highlighting the rapid convergence of Euler’s series to $e$ .

4. Examples of Use

Let’s look at some practical applications of Euler’s number, demonstrating its versatility and importance in fields ranging from finance to the natural sciences.

4.1. Instantaneous Compound Capital Calculation

Jakob Bernoulli’s insight into compound interest paved the way for understanding Euler’s number in a financial context. He observed that the value of an investment grows exponentially over time, leading to the formula $A = P \left(1 + \frac{r}{n}\right)^{nt}$ , where $A$ is the amount, $P$ is the principal, $r$ is the annual interest rate, $\boldsymbol{n}$ is the number of times the interest is compounded per year, and $t$ is the time in years.

As $\boldsymbol{n}$ approaches infinity, the expression converges to $\boldsymbol{Pe^{rt}}$ . For example, assuming for simplicity a unit initial capital $P = 1$ , $r = 0.05$ (that is 5%), and $t = 10$ years, we can use a logarithmic scale on the abscissa $n$ to observe this convergence on the ordinate $A$ :

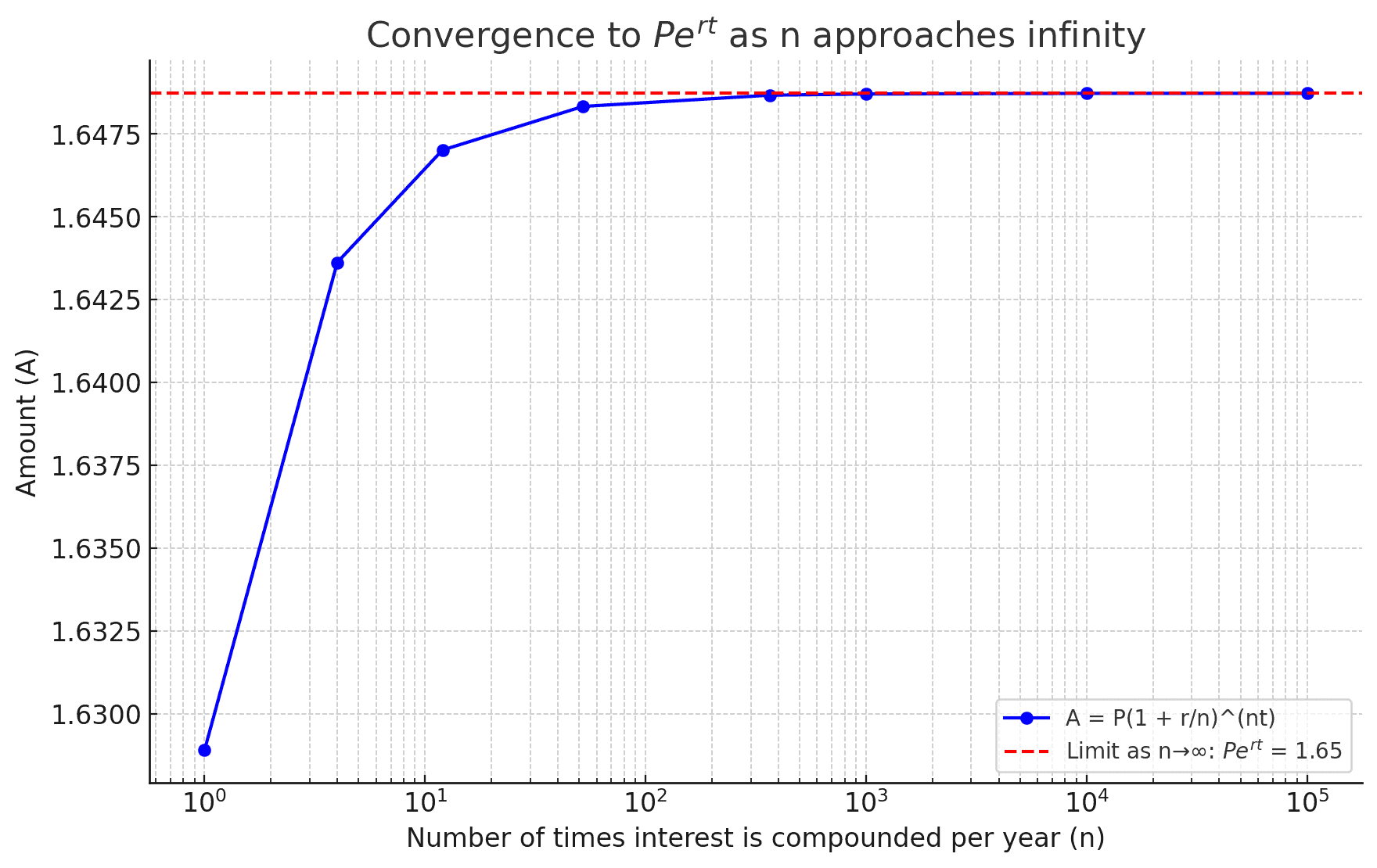This illustrates how $e$ arises naturally in the context of continuous compounding.

4.2. Calculation of Bacterial Growth

In biology, the exponential growth of bacterial populations can be modeled by the equation $\boldsymbol{N = N_0e^{kt}}$ , where $N$ is the final population size, $N_0$ is the initial population size, $k$ is the growth rate, and $t$ is the elapsed time.

For example, given an initial population $N_0 = 100$ and a growth rate $k = 0.03$ per hour, the population size after 24 hours is 205 bacteria, after 48 hours is 422 bacteria, and after 72 hours is 867 bacteria. These values are highlighted by the red dots on the graph at the corresponding time intervals:

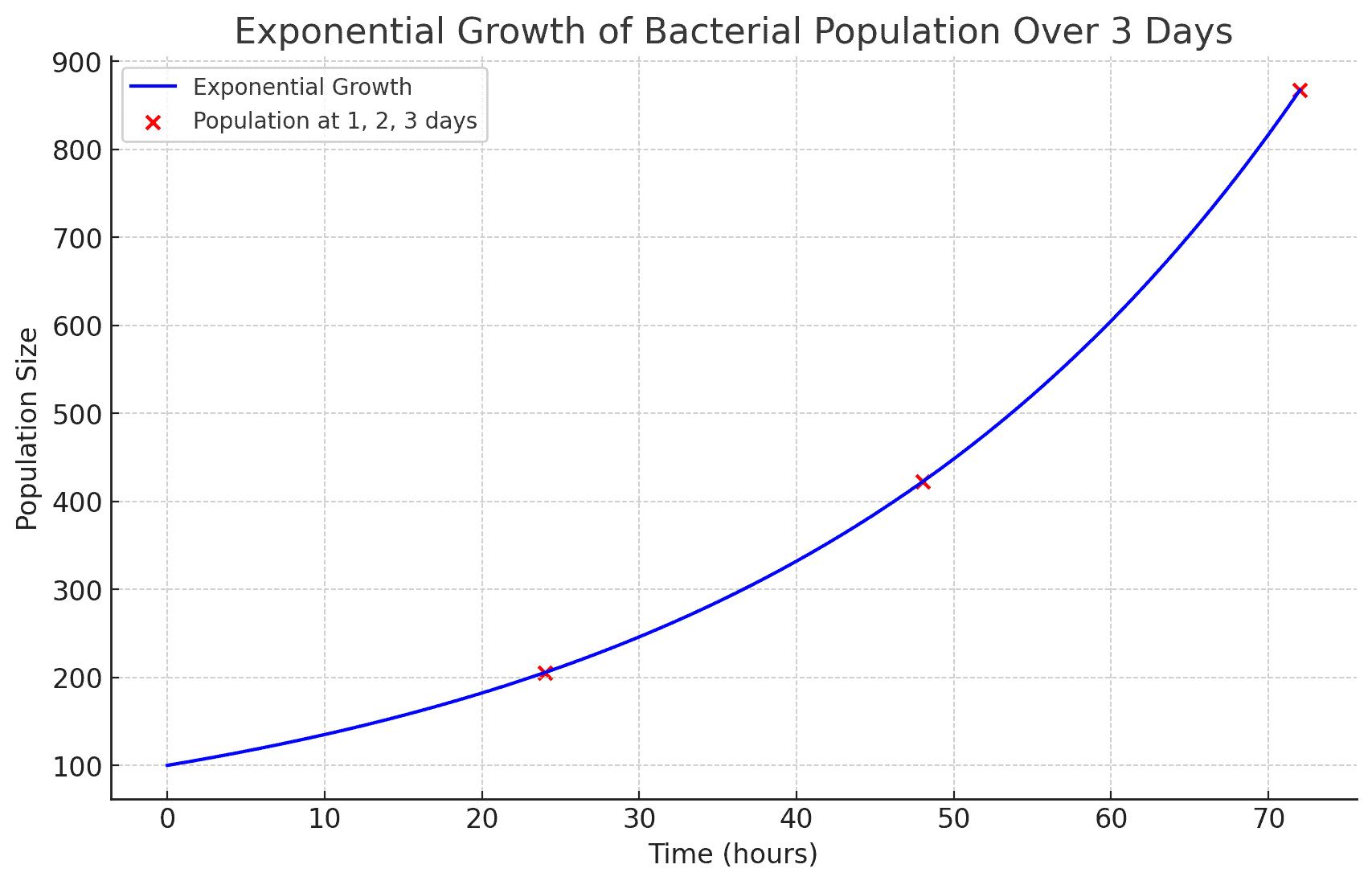This example highlights the role of $e$ in describing natural growth processes, thus emphasizing its fundamental presence in biological systems.

4.3. Radioactive Decay Law

The law of radioactive decay is $\boldsymbol{N = N_0e^{-\lambda t}}$ , where $N$ is the remaining amount of a substance, $N_0$ is the initial amount, $\lambda$ is the decay constant, and $t$ is the elapsed time.

For example, if we start with $N_0 = 100$ grams of a radioactive substance, with a decay constant $\lambda = 0.3$ per hour, only 5 grams of radioactive substance will remain after 10 hours:

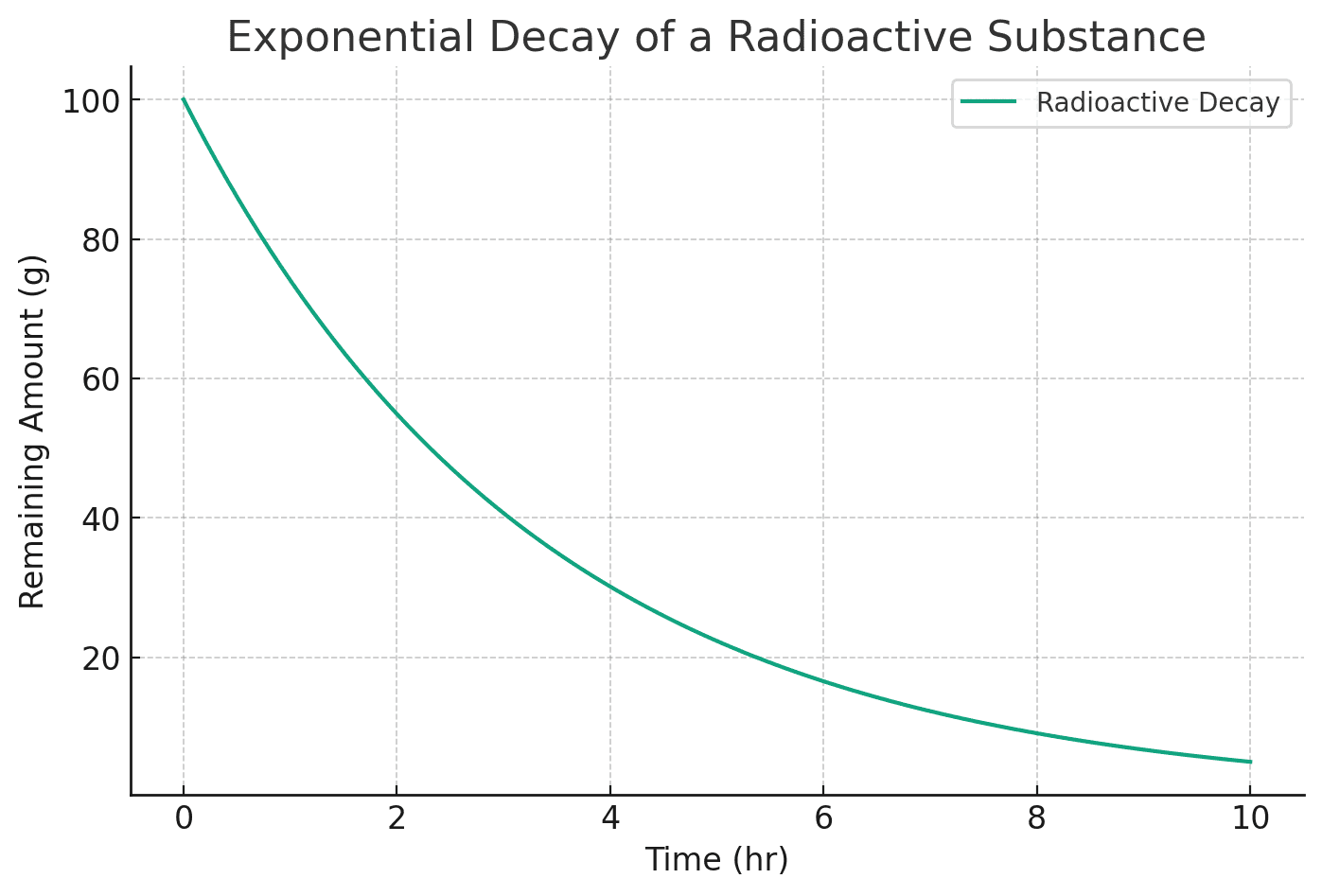This example emphasizes the utility of $e$ in quantifying the exponential decay of radioactive materials over time. This process is critical in several fields, including nuclear medicine, archaeology (carbon dating), and nuclear power generation.

4.4. Discharge of a Capacitor

Let’s consider an electronic RC circuit with a two-pole switch that we can use to charge and discharge a capacitor. This picture is from the OpenStax University Physics textbook, Volume 2, Chapter 10:

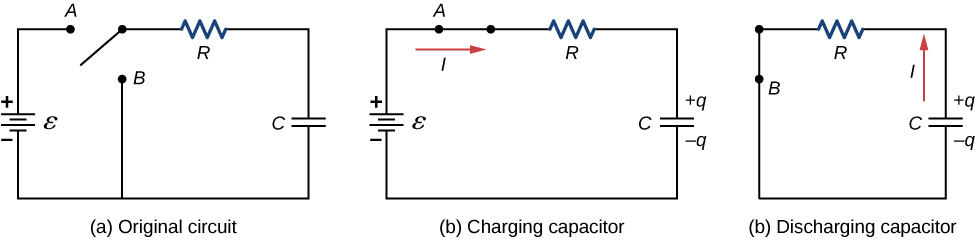
The discharge of the capacitor in this circuit is described by $\boldsymbol{Q = Q_0e^{-\frac{t}{RC}}}$ , where $Q$ is the charge at time $t$ , $Q_0$ is the initial charge, $R$ is the resistance, and $C$ is the capacitance. For example, let’s see the charge on the capacitor at any time $t$ with $Q_0 = 1 \, \text{Coulomb} \, (C)$ , $R = 10 \, \text{kiloohm} \, (k\Omega)$ , and $C = 100 \, \text{microfarad} \, (\mu F)$ :

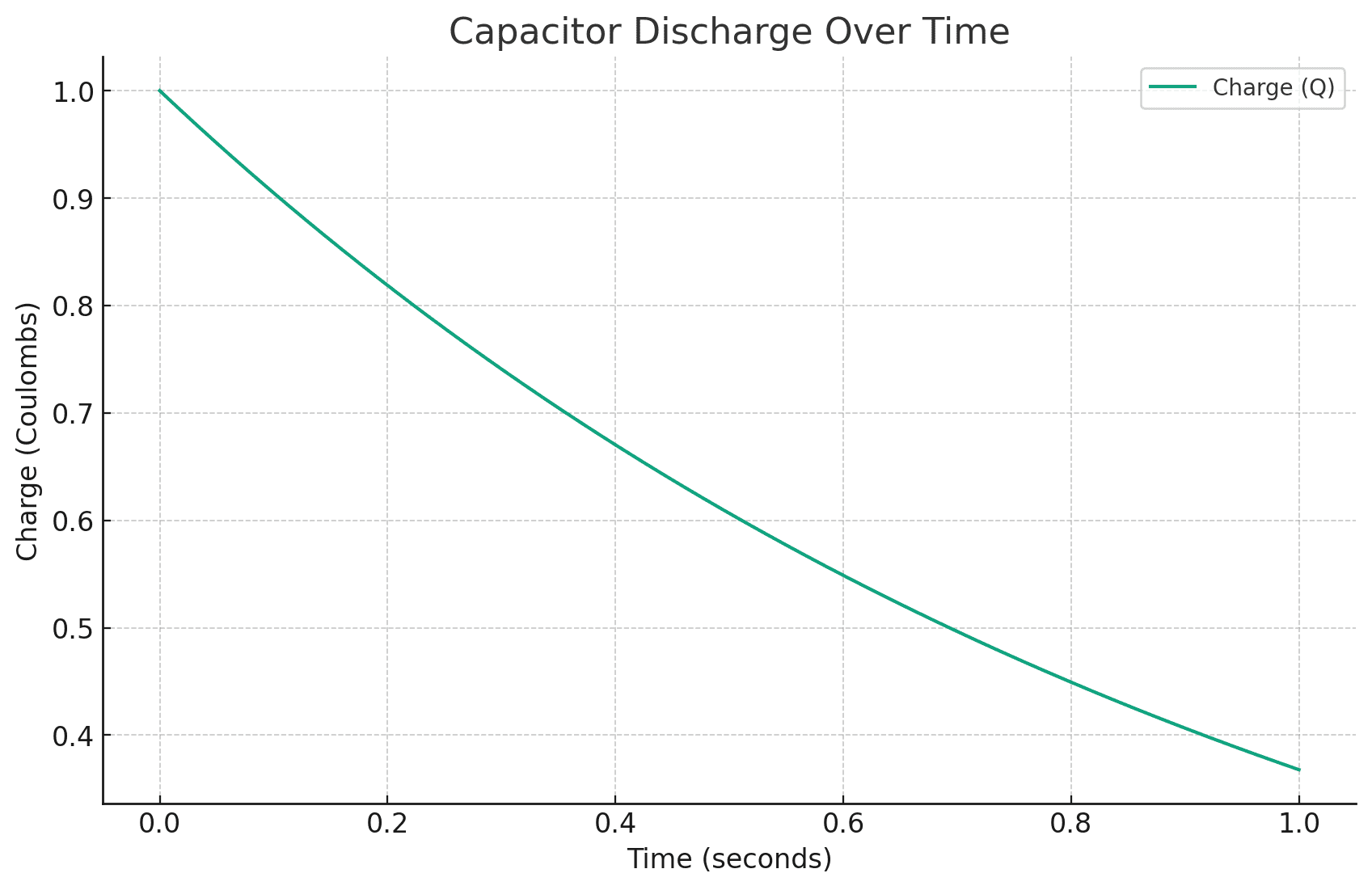This example demonstrates the role of $e$ in capturing the exponential discharge with time, thus illustrating its importance in electronics.

4.5. Shell Shape

The geometry of certain shell shapes can be modeled by the equation $\boldsymbol{r = ae^{b\theta}}$ , where $r$ is the radius from the center of the shell spiral at a given angle $\theta$ , while $a$ and $b$ are constants.

Let’s choose $a = 1$ and $b = 0.3$ for our example. The spiral starts at the center and expands outward, with the radius increasing exponentially with the angle $\theta$ :

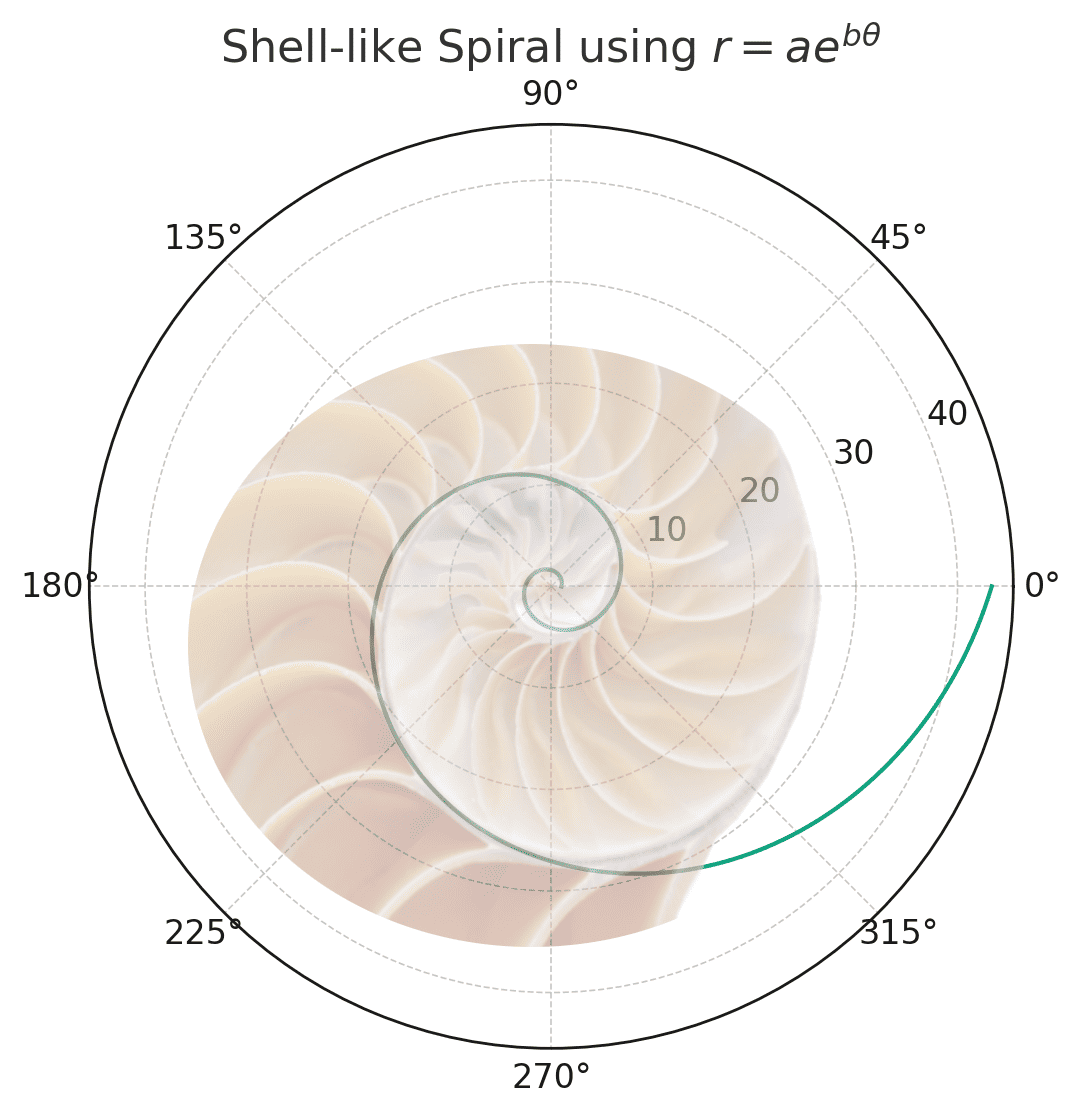We overlayed a photograph of a shell cut in two on top of the graph.

This application of $e$ in describing natural forms reveals its importance in understanding patterns and structures in nature, from the micro to the macro scale.

5. Conclusion

In this article, we’ve explored the fascinating world of Euler’s number $e$ . We’ve looked at its unique properties, its historical background, and its many applications in various disciplines.

From the exponential growth of investments to the natural patterns of growth and decay in biology and physics, $\boldsymbol{e}$ permeates both mathematical theory and the tangible realities of our world.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex