Find Cycle Start Node in a Singly Linked List | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll learn how to find a cycle starting node in a linked list. Also, we’ll analyze the different time and space complexities of each approach. Moreover, we’ll look at the most efficient algorithm and prove it. Furthermore, we’ll prove its linear time complexity. We assume having a basic knowledge of linked list data structure and Big-O notation.

2. Problem Statement

Suppose we’ve got a singly linked list. This list has a cycle. So, our task is to return a cycle start node. The only thing we are given is a linked list head (start node). Let’s look at an example for better understanding:

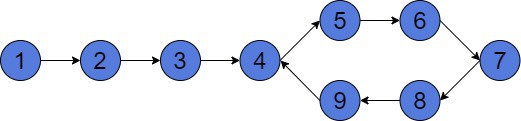
Here, the start node is 1. But, after moving forward to node 4, we go into a cycle 4 – 5 – 6 – 7 – 8 – 9 – 4. Then, after coming to the next node from node 9, we’ll start this cycle again. Moreover, we’ll never reach the end of the linked list, because it doesn’t exist. Our goal will be to return node 4 as the cycle starting node.

3. Hare and Tortoise

There are several algorithms that can help us solve this problem. For instance, we can use a HashSet. At each step, we’ll check if the current node exists in our set. If it does, then it will be the starting node of the cycle. If it doesn’t, then we’ve to add this node to the set and move to the next node. The time complexity of such a solution is $O(n)$ . However, space complexity is also $O(n)$ .

There exists another solution, that uses $O(n)$ time. But, it uses constant memory and we can reduce space complexity to $O(1)$ . This is Floyd’s Hare and Tortoise algorithm. This is a pointer algorithm, which uses a fast and slow pointer to find the cycle start node.

3.1. Idea of the Algorithm

Assume we’ve two pointers. One pointer moves twice faster than another. The slower pointer is called tortoise, for the well-known slowness of this reptile. On the other hand, the faster pointer is called hare. In our diagram, the tortoise is represented in green and the hare in red:

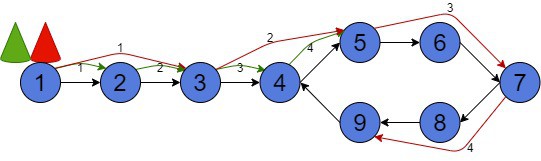
At the very beginning, they stand at the starting node 1 of the list. The tortoise will be moving one node at a time. On the contrary, the hare will move twice as fast, skipping one node. After 4 moves the hare is at node 9. However, the tortoise has just reached node 4.

Is important to notice, they both start looping infinitely. The list contains a cycle and they both enter this cycle. As a consequence, they’ll definitely meet sometime. But, we’re interested in the time period before they meet. This impacts the time complexity of the algorithm. Further, we’ll prove that they’ll meet at most after $k$ steps, where $k$ is the length of the cycle. It also means that the tortoise won’t even complete the whole cycle before their first meeting.

3.2. Explanation

The first part of an algorithm is simple, our animals will start moving until they meet. Here are the hare and tortoise separate trajectories:

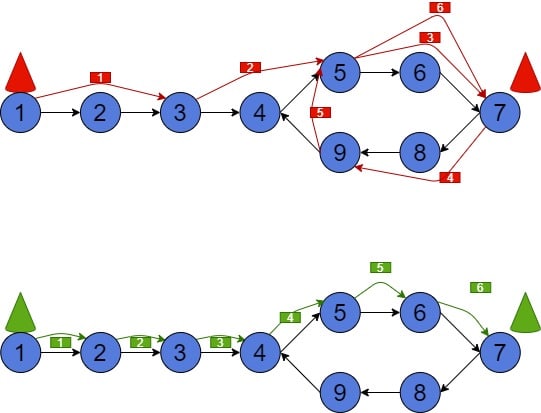
In case they move simultaneously, they’ll both meet in a cycle at node 7 after making 6 steps:

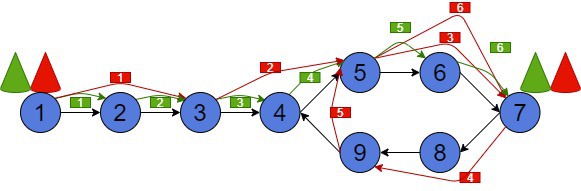
The second part of an algorithm is also simple. We move the hare to the starting position and reduce its speed twice. So, now it has the same speed as the tortoise. The tortoise continues to move from its current position. Next, they again start to move until they meet again. Interesting fact: they’ll meet at the cycle entry point, which is the answer to our problem. After that, we return this node and finish the algorithm.

We’ll prove that they’ll meet again at the node where the cycle starts in the next section. Now, let’s put the hare to the start of the list and see where they’d meet together with the tortoise:

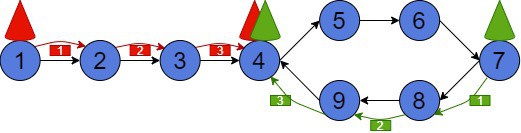
As we can see, our animals meet at node 4, which is exactly the start of the cycle.

4. Proof of Floyd’s Algorithm

The proof is a bit harder than the algorithm, but it is intuitively clear. We’ll divide the proof into three parts.

4.1. First Meet

Firstly, let’s show that they will meet after starting moving. Obviously, they’ll meet in a cycle. Suppose the length of the cycle is $k$ . When the tortoise will enter the cycle, the hair will already be in the cycle at the position $x$ . Now, we can go to another coordinate system. We’ll reduce the speed of hare and tortoise by 1. Now the tortoise won’t move and the hare will move with the speed of 1 node per 1 unit of time. There are $k - x$ nodes between them. The hare will reach the tortoise in $k - x$ steps.

Let’s think about their real speed. The hare moves twice faster than the tortoise. Therefore, it means, the above-mentioned speed transformations simulate the same situation.

4.2. Intuitive Explanation

Now we’ve their first meeting point in a loop at the position $x$ . According to the algorithm, we must reduce the hare’s speed and move it to the beginning of the list. And when they’ll meet again, the meeting point will be the cycle start node.

Suppose $M$ to be the length of the list from the starting node $s_{0}$ to the loop entrance $s$ . Let also $L$ be the length of the cycle. The hare and the tortoise meet at node $x$ in the loop. Let $Y$ be the distance from $s$ to $x$ . And let $Z$ be the distance from $x$ to $s$ :

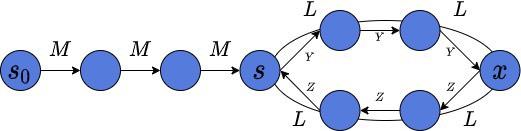
Further, we’ll prove $M = a \times L + Z$ . This will help us to explain now why our pointers would meet at the start of the cycle.

We transfer the hare after meeting at $x$ to the start of the list before they start to move again simultaneously. The tortoise will make $a$ loops and appear at $x$ again. It’ll have to make $Z$ steps to reach the beginning of the cycle. Is important to remember, we reduce the hare’s speed to be equal to the tortoise one. Thus, the hare will make $a \times L$ steps from $s_{0}$ and then will have $Z$ steps left to the cycle beginning $s$ , same as the tortoise. But, it works if and only if when $M = a\times L + Z$ , where $a$ is a constant value.

4.3. Formal Proof

We’ll prove that $M \mod L = Z$ , where $\mod$ is the modulo operation. It simply means that we can divide $M$ by $L$ , and the remainder after division will be Z. This will help to prove that animals will meet again at $s$ . If $M \mod L = Z$ , then we’re able to reproduce the animals’ movement, mentioned in the previous sub-section. Imagine, distance M might be very long. By proving $M \mod L = Z$ , we’ll show that $M = a \times L + Z$ .

Before animals’ first meet, the hare’s distance will be $H_{1} = M + a \times L + Y$ . $a$ is a constant value. If $M$ is very long, then the hare will make many loops in a cycle waiting for the tortoise. Meanwhile, the tortoise distance is $T_{1} = M + Y$ . In case the tortoise is twice slower than the hare, we can make up equality:

$2 \times T_{1} = H_{1}$ , or $2 * (M + Y) = M + a * L + Y$ . It is equal to $M + Y = a * L$ . Is important to remember, that $Y = L - Z$ .

Thus, $M + L - Z = a * L$ , or $M = (a - 1) * L + Z$ .

Taking $\mod L$ on both sides of the equality we get $M \mod L= ((a - 1) * L + Z) \mod L$ $= (a - 1) * L \mod L + Z \mod L = 0 + Z \mod L = Z \mod L$ .

Finally, we’ve just proved that $M \mod L = Z$ . It means Floyd’s algorithm works.

5. Time and Memory Complexity

As we can notice, we use constant space complexity, which is just two pointers: hare and tortoise.

The time complexity of the algorithm is $O(n)$ , where $n$ is the number of nodes in a list. The time complexity is linear, in case we’d make no more than $n + k$ steps with our pointers before their first meet. $k$ is the length of the cycle and $k \leq n$ . Therefore, the first part takes $O(n)$ time. The second part of an algorithm will also take $O(n)$ steps. Thus, the final time complexity is $O(n) + O(n) = O(n)$ .

6. Conclusion

In this article, we’ve discussed approaches to finding the cycle start node in a linked list. Moreover, we’ve explained and proved the most efficient algorithm to solve this problem. Furthermore, we’ve given an intuitive explanation of the proof. The two-pointer approach is a popular technique, which can be used in many algorithmic problems. For instance, the same hare and tortoise might help us find the duplicate number in an array.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex