1. Overview
In this tutorial, we’ll talk about how to convert a color from HSL to RGB. First, we’ll make a brief introduction to color models focusing on the HSL and RGB color space and then we’ll present a method to convert from HSL to RBG along with a detailed example.
2. Color Models
In order to use color in any computing device, we need to represent it as a vector of numerical values. To do this, we define color models which are mathematical models that map colors to a set of integers. There are many proposed color models that are suitable for different applications. In this tutorial, we’ll focus on the HSL and the RGB color model.
2.1. HSL
HSL is a color model that was proposed because it is very closely aligned to the way human vision perceives a color. It is very popular in computer graphics and consists of three components namely hue, saturation, and lightness.
HSL color model can be represented as a cylinder where the hue is an angular dimension starting at the red color at 0°, going through the green color at 120° and the blue color at 240°. The vertical axis corresponds to lightness where at the bottom we have zero lightness (black) and at the top we have full lightness (white). The last axis (horizontal) corresponds to saturation where pure colors are around the outside edge of the cylinder where saturation is equal to 1.
The above representation is shown in the image below:
2.2. RGB
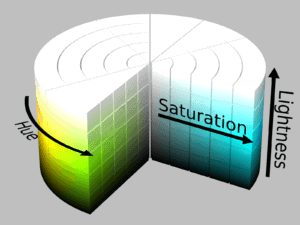
RGB is the main color model that is used to display and represent an image in any electronic device nowadays. It stands for Red, Green, Blue since these are the primary colors that are mixed to represent any RGB color.
In RGB, a color is defined using three integer values (one for each primary color) ranging from 0 to 255. A value of zero corresponds to dark while a value of 255 to bright.
In the image below, we can see the RGB cube:
3. Method
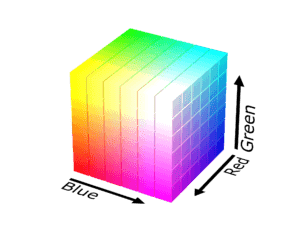
Now, we’ll present a method to convert an HSL color representation to an RGB one. Let’s suppose that we have a color with values H, S and L where:
![H \in [0^\circ, 360^\circ]](/wp-content/ql-cache/quicklatex.com-f9157edada14f367b8505756ce7f9e6d_l3.svg "Rendered by QuickLaTeX.com")
![S \in [0, 1]](/wp-content/ql-cache/quicklatex.com-8ddf666edbd372ac3c0f6dd457220599_l3.svg "Rendered by QuickLaTeX.com")
![L \in [0, 1]](/wp-content/ql-cache/quicklatex.com-650a79150c1705757c5ae43e09a5617a_l3.svg "Rendered by QuickLaTeX.com")
First, we compute chroma which is defined as:
Our next step is to search for a point (
) in one of the three faces of the RBG cube that has the same hue value and chroma value as our color. To do this, we first compute 
and 
as follows:
where 
corresponds to the remainder of the euclidean division of 
with 2. Then, the point we search for is defined as:
The final step is to find the correct amount of lightness for our RGB color. To achieve this we add the same value 
to each RGB component where:
So, the converted RGB color is equal to 
.
4. Example
Now, we’ll apply the above equation in a simple example to better understand the conversion algorithm.
Let’s suppose that we have a color with 
and apply the previous series of equations:
So, the respective RBG color is equal to 
.
5. Conclusion
In this article, we presented a method that converts a color from HSL to RGB. First, we made an introduction to the color models and then we talked about the conversion method along with a simple example.